Особенности тока смещения. Ток смещения эквивалентен току проводимости только в отношении способности создавать магнитное поле

Ток смещения эквивалентен току проводимости только в отношении способности создавать магнитное поле. Ток смещения существует лишь там, где меняется со временем электрическое поле. В диэлектриках ток смещения состоит из двух существенно различных слагаемых, так как вектор электрического смещения 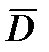равен

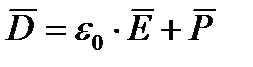
Где 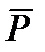- вектор поляризованности, то отсюда видно плотность тока смещения 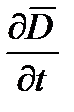складывается из «истинного тока» смещения 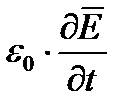и тока поляризации 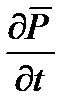– величины, обусловленной движением связанных зарядов. Токи поляризации так же как токи смещения возбуждают магнитное поле. Принципиально новое содержится в том, что другая часть тока смещения 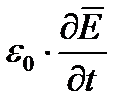, которая не связана ни с каким движением заряда, обусловлена только изменением электрического поля, так же возбуждает магнитное поле. Открытие этого явления – наиболее существенный и решающий шаг, сделанный Максвеллом при построении теории электромагнитного поля. Это открытие аналогично открытию электромагнитной индукции, согласно которому переменное магнитное поле (изменяющееся) возбуждает вихревое электрическое поле.

3.Основные уравнения переменного электрического поля.

1.Определение переменного электрического поля. Под переменным электрическим пол понимают совокупность изменяющихся во времени. Взаимно связанных и обуславливающих друг друга электрического и магнитных полей. Оно определяется двумя векторными величинами – напряженности электрического поля 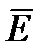и напряженностью магнитного поля .

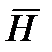Переменное электромагнитное поле является одним из видов материи. Оно обладает энергией, массой, количеством движения. Может превращаться в другие виды материи и самостоятельно существовать в виде электромагнитных волн. При исследовании процессов в переменном электрическом поле используют уравнение Максвелла.

2.Уравнение Максвелла в интегральной форме.

Открытие тока смещения 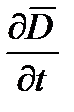позволили Максвеллу создать единую теорию электрических и магнитных явлений в виде системы фундаментальных уравнений электродинамики, называемых уравнениями Максвелла в неподвижных средах. В интегральной форме системы уравнений Максвелла имеют следующий вид:

Пояснение (1):

(1) 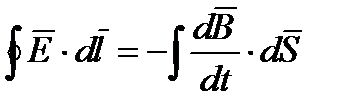a) сравнение в потенциальном безвихревом поле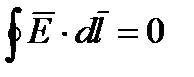

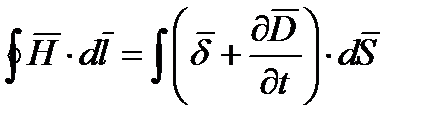(2) 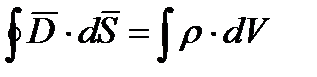б) в вихревом электрическом поле, индуцированном изменяющимися моментами полей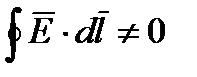

(3) в) т.е вихревое моментное напряжение порождает электриче ское поле

(4)

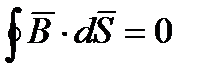
где 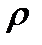- объемная плотность сторонних зарядов;

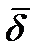- вектор плотности тока проводимости.

Эти уравнения в такой форме выражают всю совокупность сведений об электрическом поле.

(1) Циркуляция вектора электрической напряженности 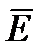по замкнутому контуру равна со знаком «минус» производной по времени от магнитного потока через любую поверхность, ограниченную данным контуром. При этом под 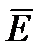понимают не только вихревое электрическое поле, но и электростатическое (циркуляция которого равна нулю).

(2) Поток вектора электрического смещения 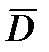сквозь любую замкнутую поверхность равен алгебраической сумме сторонних зарядов, охватываемых этой поверхностью.

(3) Циркуляция вектроа 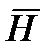по любому замкнутому контуру равна полному току (току проводимости и току смещения) через произвольную поверхность, ограниченную данным контуром.

(4) Поток вектора магнитной индукции 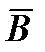сквозь произвольную электрическую поверхность всегда равен нулю. Из уравнения Максвелла для циркуляции векторов 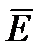и 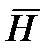следует, что электрические и магнитные поля нельзя рассматривать как независимые: изменение во времени одного из этих полей приводит к появлению другого. Поэтому имеет смысл лишь совокупность этих полей, описывающая единое электромагнитное поле.

Есть поля стационары 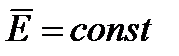и 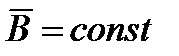, то уравнения Максвелла распадаются на две группы независимых уравнений:

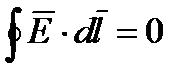
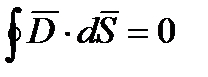Пояснение: т.е существуют условие, когда электрические и магнитные поля независимы друг от друга

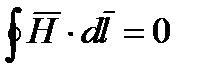
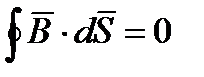
В этом случае электрическое и магнитное поля независимы друг от друга, ч то и позволило нам вначале изучать постоянное электрическое поле, а затем постоянное магнитное поле.

Уравнения Максвелла являются постулатами электродинамики. До сих пор их не доказать ни кому. Они могут быть подтверждены в натоящее время только опытным путем.