Электрическое поле постоянного тока в проводящей среде.
- Плотность тока и ток.
Упорядоченное движение свободных электронов в металле и ионов в жидкости под действием внешнего электрического поля называется током проводимости. Свойство среды, характеризующее ее способность проводить ток, называют удельной проводимостью (гамма), она зависит от физических свойств проводящего материала и температуры и имеет размерность 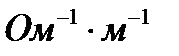 . *****
. *****
Основной величиной электрическом поле проводящей среды является плотность тока 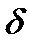 (дельта). Это векторная величина, направленная по напряженности поля
(дельта). Это векторная величина, направленная по напряженности поля 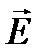 и численно равная отношению тока
и численно равная отношению тока  , протекающего через элемент поверхности
, протекающего через элемент поверхности 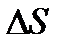 (перпендикулярный к направлению напряженности поля в данной точке), к величине
(перпендикулярный к направлению напряженности поля в данной точке), к величине 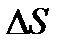 этой поверхности.
этой поверхности.
Дельта 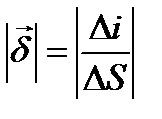
Если поверхность 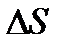 имеет конечные результаты, то направление вектора плотности тока во всех элементах, на которые могла быть разбита эта поверхность, и направление элементов поверхности может быть различным, и ток определится как
имеет конечные результаты, то направление вектора плотности тока во всех элементах, на которые могла быть разбита эта поверхность, и направление элементов поверхности может быть различным, и ток определится как
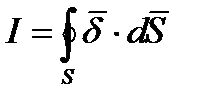
Таким образом, ток есть поток вектора плотности тока. В отличие от плотности тока, ток является скаляром алгебраического характера.
- Первый закон Кирхгофа в дифференциальной форме.
Если в проводящей среде выделить некоторый объем, по которому протекает постоянный не изменяющийся во времени ток, то можно сказать, что ток, который войдет в объем должен равняться току, вышедшему из объема, иначе бы в этом объеме происходило бы накопление электрических зарядов, что опыт не подтверждает. Сумму входящего в объем и выходящего из объема токов записывают как:
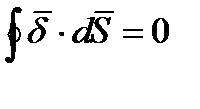
Если разделить левую и правую часть этого выражения на одно и то же число (объем), то
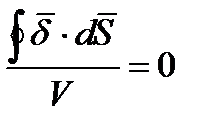
Очевидно, будет справедливым и равенство
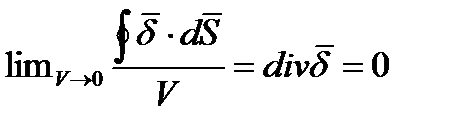
Таким образом, для постоянного, неизменного во времени поля в проводящей среде
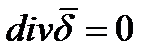
Это соотношение называют первым законом Кирхгофа в дифференциальной форме. Оно означает, что в установившемся режиме (при постоянном токе) любой точке поля нет ни истока, ни стока линий тока проводимости  . Так же этот закон утверждает о принципе непрерывности линии тока.
. Так же этот закон утверждает о принципе непрерывности линии тока.
3. Электрическое поле в области тока.Аналогия между полем в проводящей среде и электростатическим полем.
По своей природе электростатическое поле и поле постоянного тока в проводящей среде различно. Электростатическое поле создается электрическими зарядами, неизменными во времени и неподвижными в пространстве, тогда как электрическое поле в проводящей среде есть поле, в котором электрические заряды имеют упорядоченное движение под действием внешнего источника. Тем не менее, между двумя полями может быть проведена определенная формальная аналогия. Действительно, электростатическое поле в областях, незанятых зарядами удовлетворяет уравнению Лапласа. Электрическое поле постоянного тока в проводящей среде вне сторонних источников то же ему удовлетворяет. В обоих случаях имеют дело с вектором напряженности поля 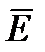 . С вектором электрического смещения
. С вектором электрического смещения 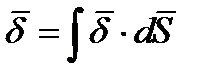 можно сопоставить вектор плотности тока. С потоком вектора
можно сопоставить вектор плотности тока. С потоком вектора 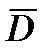 (обозначим его
(обозначим его 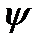 )
) 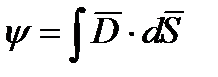 можно сопоставить поток вектора плотности электрического тока
можно сопоставить поток вектора плотности электрического тока 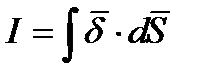 .
.
Граничные условия на поверхности двух диэлектриков 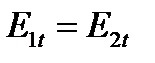 и
и 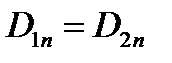
Граничные условия на поверхности раздела двух сред с различной проводимостью:

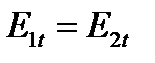 и
и 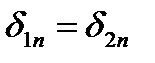
Но если два поля удовлетворяют одному и тому же уравнению 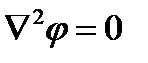 и в них выполняются тождественные граничные условия для исходных величин, то при одинаковой форме граничных поверхностей на основании теоремы единственности можно сказать, что совокупность силовых и эквипотенциальных линий в этих двух полях (то есть картина поля) будет одинаковой.
и в них выполняются тождественные граничные условия для исходных величин, то при одинаковой форме граничных поверхностей на основании теоремы единственности можно сказать, что совокупность силовых и эквипотенциальных линий в этих двух полях (то есть картина поля) будет одинаковой.
- Закон Ома в дифференциальной форме. Второй закон Кирхгофа в дифференциальной форме.
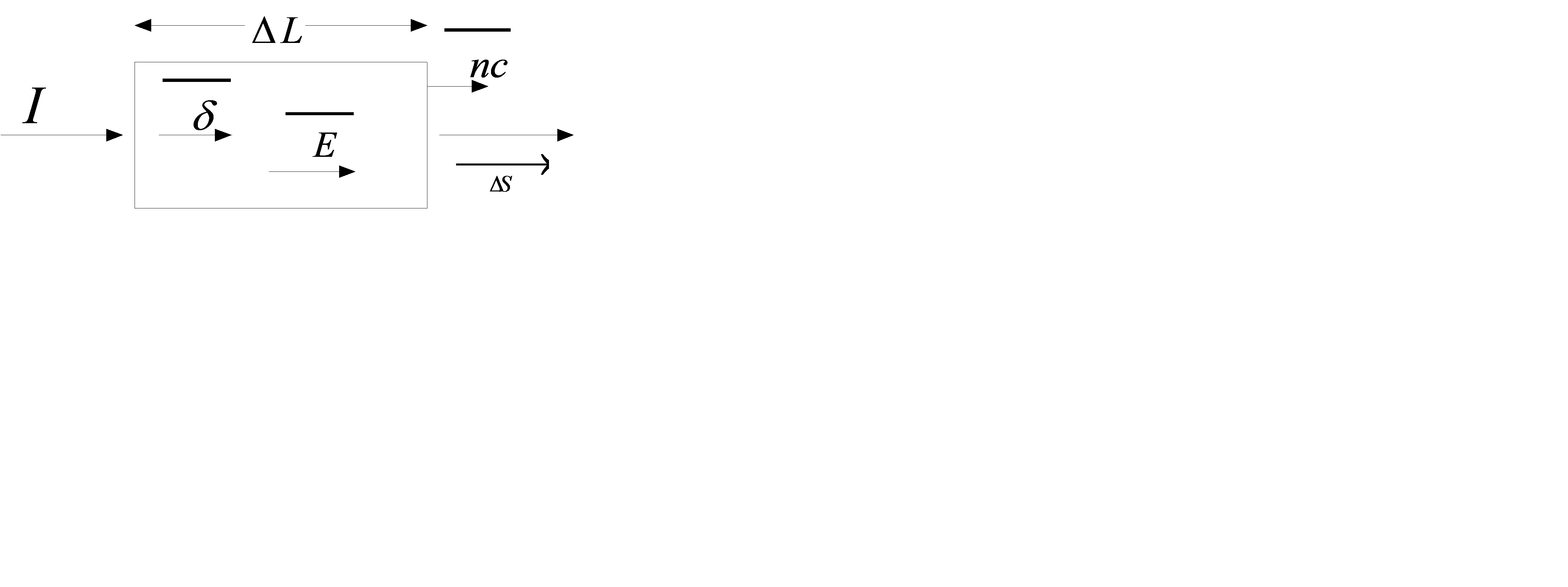 Выделим в проводящей среде небольшой параллепипед объемом
Выделим в проводящей среде небольшой параллепипед объемом 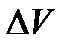 . Длина ребра параллепипеда
. Длина ребра параллепипеда 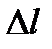 , площадь поперечного сечения
, площадь поперечного сечения 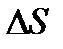 . Расположим этот паралеппипед так, чтобы напряженность поля в нем была направлена параллельно ребру
. Расположим этот паралеппипед так, чтобы напряженность поля в нем была направлена параллельно ребру
В силу малости объема можно считать, что напряженность электрического поля 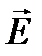 одна и та же во всем элементарном объеме. Тогда
одна и та же во всем элементарном объеме. Тогда 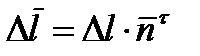 ;
; 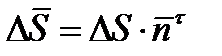
где 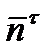 - единичный вектор по направлению
- единичный вектор по направлению 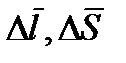 и
и 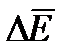
Ток 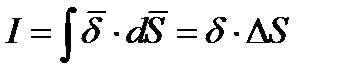 (а)
(а)
Напряжение на элементе объема 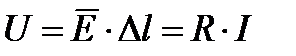 (Закон Ома)
(Закон Ома)
Сопротивление элемента объема 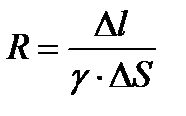 (б)
(б)
Подставив в выражение 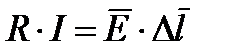 эквиваленты R и I, получим
эквиваленты R и I, получим 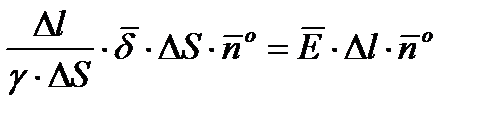
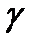 - удельная проводимость (гамма)
- удельная проводимость (гамма)
Откуда 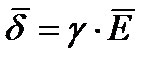 (4.1)
(4.1)
Соотношение (4.1) называют законом Ома в дифференциальной форме. Оно устанавливает связь между плотностью тока 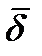 в данной точке проводящей среды и напряженностью поля в этой же точке. Уравнение (4.1) справедливо для областей в не источников Э.Д.С. В областях занятых источниками Э.Д.С. кроме кулонова (электрического) поля, существует так называемая стороннее электрическое поле, обеспечивающее непрерывное движение зарядов в электрической цепи.
в данной точке проводящей среды и напряженностью поля в этой же точке. Уравнение (4.1) справедливо для областей в не источников Э.Д.С. В областях занятых источниками Э.Д.С. кроме кулонова (электрического) поля, существует так называемая стороннее электрическое поле, обеспечивающее непрерывное движение зарядов в электрической цепи.
Под сторонним электрическим полем понимают электрическое поле не электростатической природы (например, обусловленное химическим, механическими или иными процессами). Напряженность стороннего поля обозначают 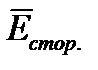 . В областях, занятых источниками Э.Д.С., полное значение напряженности поля равно геометрической сумме
. В областях, занятых источниками Э.Д.С., полное значение напряженности поля равно геометрической сумме
Напряженностей кулонова и стороннего полей : 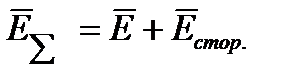

(кулоново поле всегда направлено от (+) к (-)):
На рисунке схематически изображена электрическая цепь постоянного тока. Она состоит из источника питания и нагрузки. Линейный интеграл от сторонней напряженности поля внутри источника называется Э.Д.С. источника ( 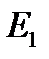 ):
):
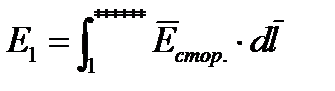
Под действием стороннего поля в источнике непрерывно происходит разделение электрических зарядов. Положительные заряды перемещаются к «+» источника, а отрицательные к «-». Поле, созданное в проводящей среде разделившимися зарядами называется кулоновым полем. Внутри источника кулонова поля направлено навстречу стороннему полю. Полное значение напряженности поля внутри источника равно 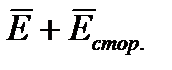 . Вне источника кулоново поле направлено от положительного электрода к отрицательному. Под действием этого поля и происходит упорядоченные движения зарядов в области вне источника. При протекании поля по цепи
. Вне источника кулоново поле направлено от положительного электрода к отрицательному. Под действием этого поля и происходит упорядоченные движения зарядов в области вне источника. При протекании поля по цепи 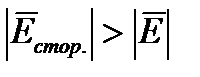 . При разомкнутой цепи
. При разомкнутой цепи 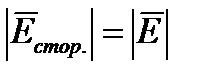 .
.
Закон Ома в дифференциальной форме для областей занятых источниками Э.Д.С. записывается так:
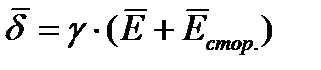 (4.2)
(4.2)
Уравнение (4.2) называется обобщенным законом Ома в дифференциальной форме. Или второй закон Кирхгофа в дифференциальной форме. Если от обеих частей уравнения (4.2) взять интеграл по замкнутому контуру, включающему в себя источник Э.Д.С., то из этого уравнения будет получен второй закон Кирхгофа. (Сумма подтекающих к любому узлу токов равна сумме утекающих от узла токов). По этому уравнение (4.2) называется вторым законом Кирхгофа в дифференциальной форме.
- Дифференциальная форма Джоуля – Ленца.
Если по проводнику сопротивления R протекает постоянный ток I, то в единицу времени (сек) в нем выделяется энергия 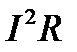 . Определим энергию, выделяющуюся в единицу времени в единице объема проводящей среды.
. Определим энергию, выделяющуюся в единицу времени в единице объема проводящей среды.

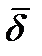 - вектор плотности тока
- вектор плотности тока
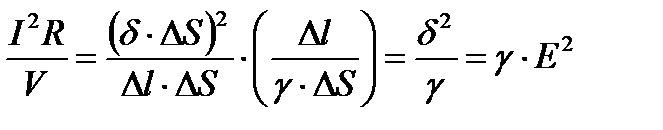 т.к
т.к  и
и 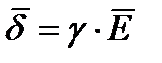
Следовательно в единице объема проводящей среды выделяется в единицу времени энергия, численно равная
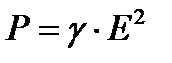
Лекция №5.
- Уравнение Лапласа для электрического поля в проводящей среде.
Это уравнение описывает потенциал в области тока и его связь с напряженностью. Так же как в электростатическом поле, напряженность электрического поля в проводящей среде
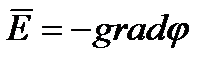 .
.
В неизвестном во времени поле 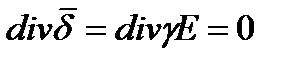
Если 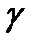 среды (удельная проводимость) не изменяется от точки к точке, то есть среда однородна и изотропна, то
среды (удельная проводимость) не изменяется от точки к точке, то есть среда однородна и изотропна, то 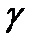 , как постоянную величину, можно вынести за знак дивергенции и, следовательно, вместо
, как постоянную величину, можно вынести за знак дивергенции и, следовательно, вместо 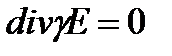 можно написать
можно написать
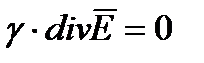 или
или
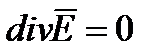 т.е и т.к
т.е и т.к 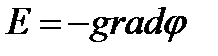
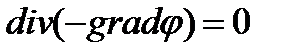 или
или
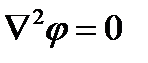
Таким образом сделаем важный вывод: поле в однородной проводящей среде подчиняется уравнению Лапласа. Поле постоянного тока в проводящей среде является потенциальным. В нем, в областях, не занятых источниками,

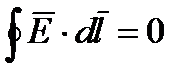 - это предпосылка для вывода граничных условий
- это предпосылка для вывода граничных условий
Или циркуляция вектора 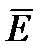 вдоль любого замкнутого контура равно нулю.
вдоль любого замкнутого контура равно нулю.
- Переход тока из сферы с одной проводимостью
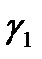 в среду с другой проводимостью
в среду с другой проводимостью 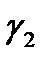 . Граничные условия.
. Граничные условия.
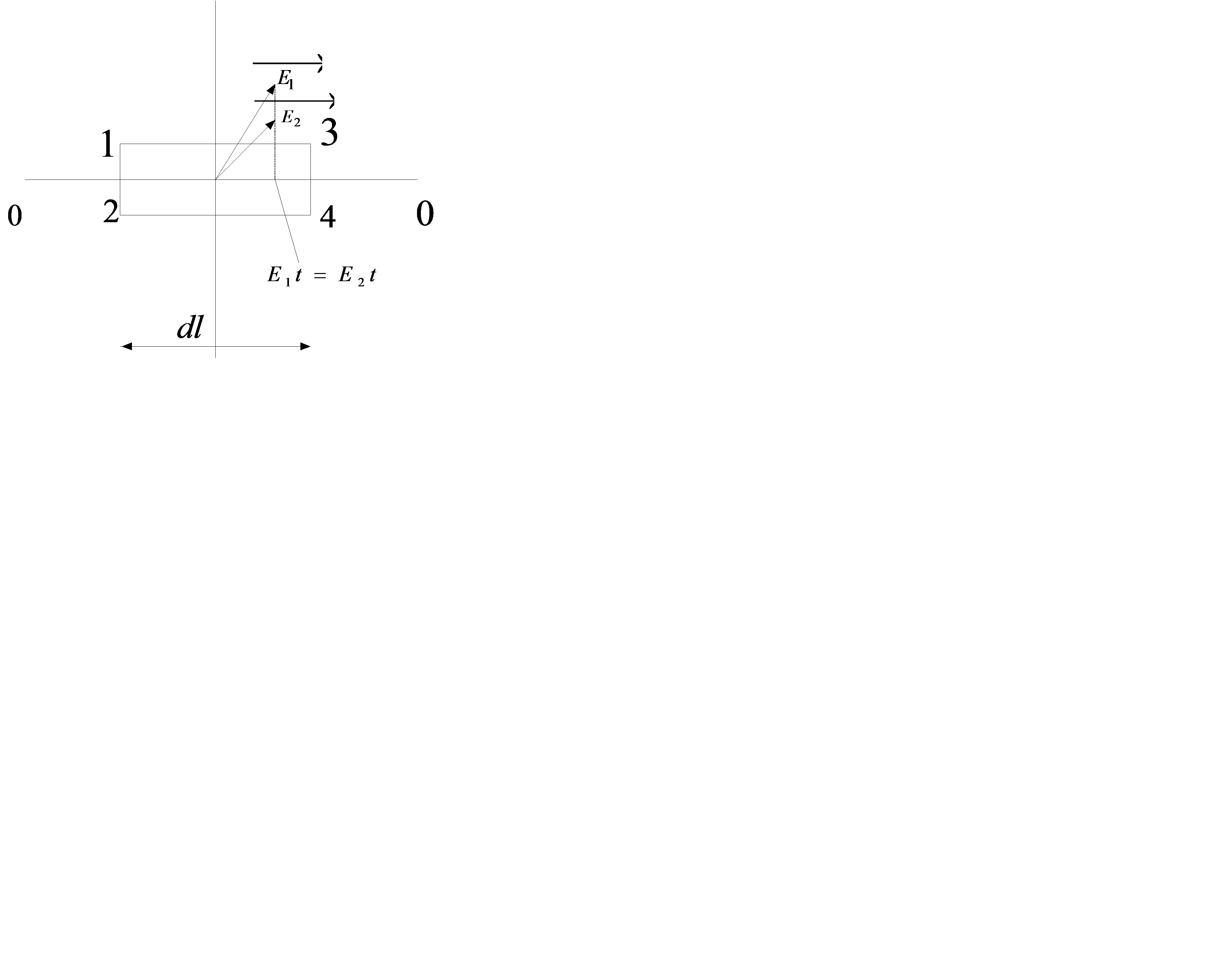 Выясним, какие граничные условия выполняются при переходе тока из среды с одной проводимостью в среду с другой проводимостью. Построим рисунок границы раздела двух сред.
Выясним, какие граничные условия выполняются при переходе тока из среды с одной проводимостью в среду с другой проводимостью. Построим рисунок границы раздела двух сред.
На рисунке линия 00 есть граница раздела двух сред. Возьмем на границе плоский замкнутый контур 1234. Составим циркуляцию вдоль этого контура. Стороны 12 и 34 его весьма малы по сравнению со сторонами 23 и 41. Обозначим длину стороны 23 и 41 через dl.
Так как циркуляция вектора напряженности 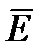 вдоль любого замкнутого контура равна нулю
вдоль любого замкнутого контура равна нулю 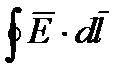 , то она равна нулю и для контура 1234.
, то она равна нулю и для контура 1234.
В силу малости отрезков 12 и 34 пренебрежем составляющими интеграла вдоль этих путей и тогда
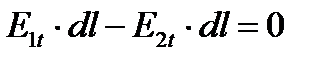 или
или 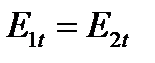
То есть тангенциальные составляющие напряженности поля на границе раздела двух сред равны. Это совпадает первым граничным условием на границе раздела двух сред.
Докажем второе свойство: на границе раздела равны нормальные составляющие плотностей токов. Построим рисунок границы раздела двух сред.
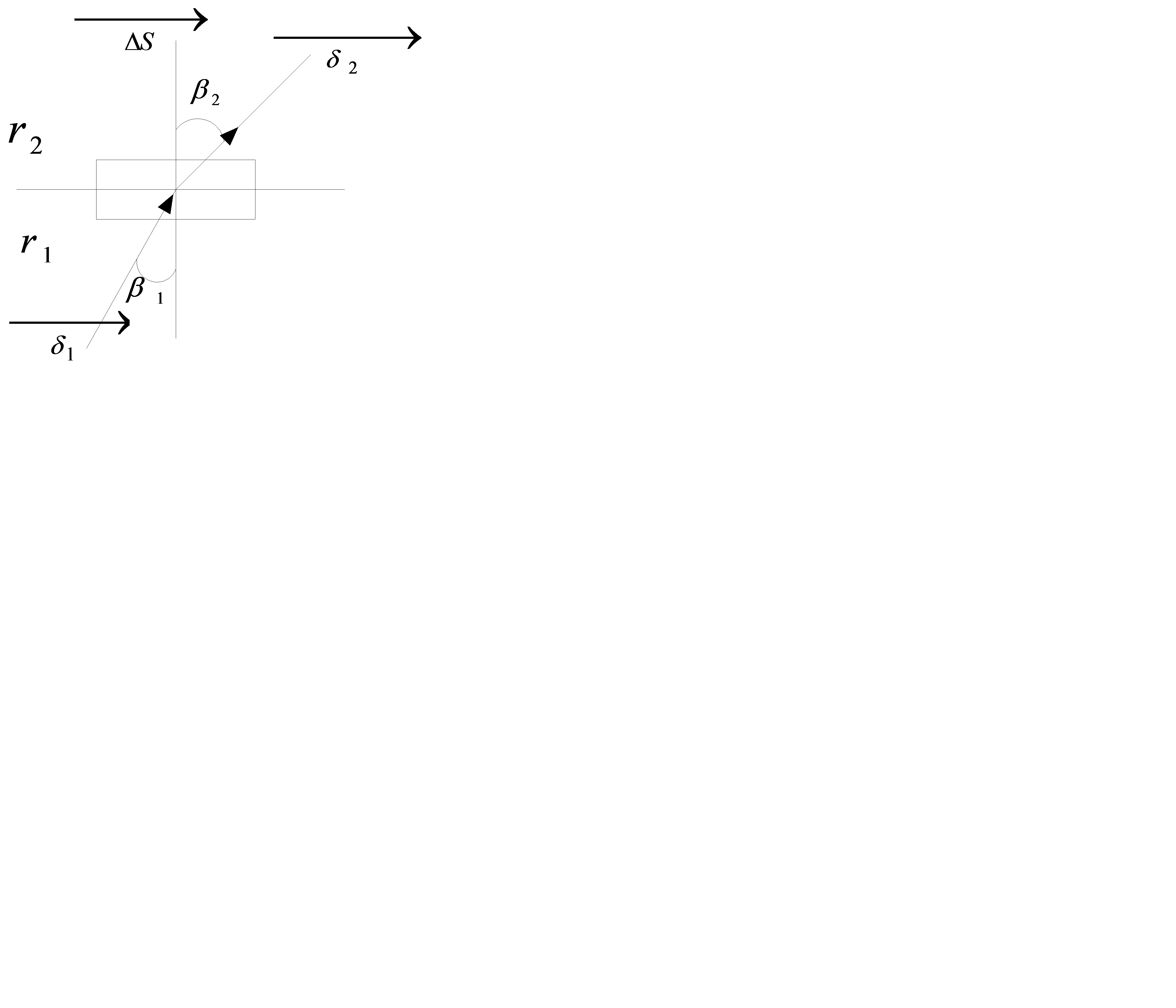
На границе раздела выделим сплющенный параллепипед. Поток вектора 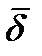 , втекающий в его объем через нижнюю грань, равен
, втекающий в его объем через нижнюю грань, равен 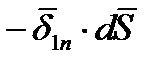
Поток вектора вытекающий из объема через верхнюю грань равен 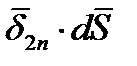
Так как циркуляция вектора плотности тока по замкнутой поверхности равна нулю
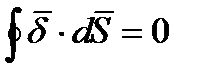 , считаем площади боковых граней
, считаем площади боковых граней 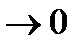 и отсюда
и отсюда 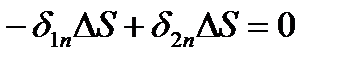
и отсюда нормальные плотности тока впервой и второй средах равны 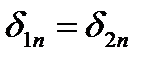
отсюда сделаем общие выводы.
1). При переходе тока из среды с одной проводимостью в среду с другой проводимостью непрерывная тангенциальная составляющая вектора 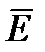 , то есть
, то есть 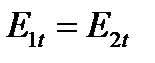 .
.
В общем случае нормальные составляющие векторов напряженности не равны. 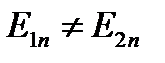
2). При переходе тока из среды с одной проводимостью в среду с другой проводимостью непрерывна нормальная составляющая плотности тока 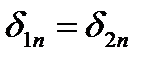 , но в общем случае тангенциальные составляющие плотностей тока не равны
, но в общем случае тангенциальные составляющие плотностей тока не равны 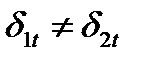
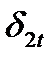 Отсюда следует, что полные значения вектора напряженности
Отсюда следует, что полные значения вектора напряженности 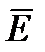 и вектора плотности тока
и вектора плотности тока 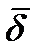 в общем случае меняются скачком на границе раздела двух сред. Найдем связь между углом падения
в общем случае меняются скачком на границе раздела двух сред. Найдем связь между углом падения 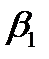 и углом преломления
и углом преломления 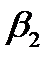 :
:
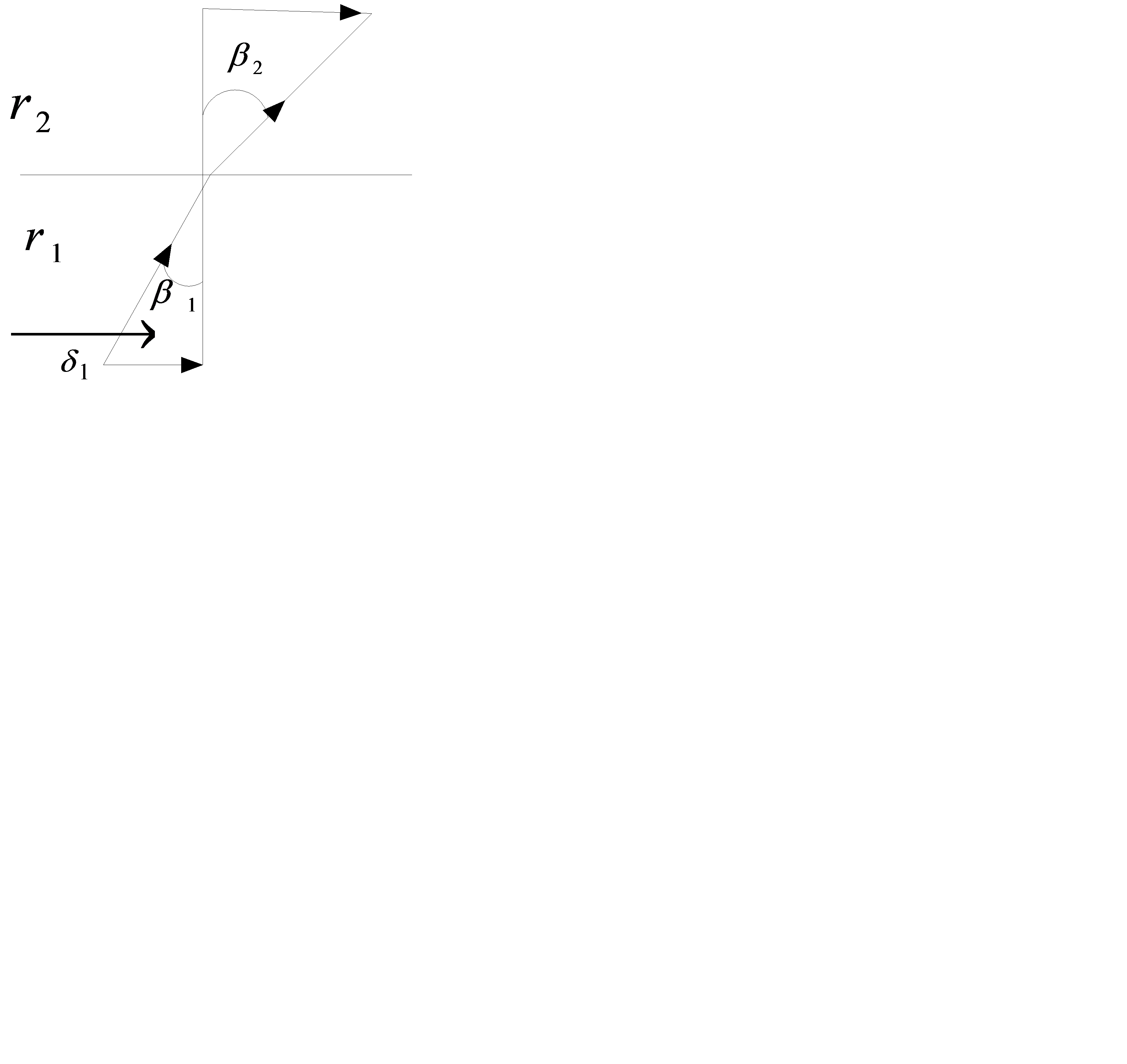
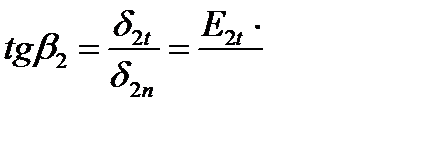
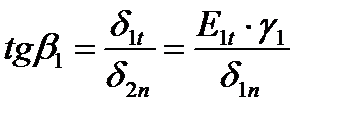
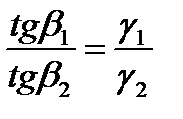
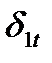
Отношение тангенсов угла падения к углу преломления равно отношению удельных проводимостей первой среды ко второй.
Если ток переходит из среды с большой проводимостью (например: из металла) в среду с малой проводимостью (например: в землю), то тангенс угла преломления 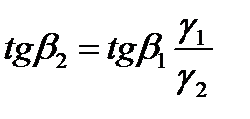 меньше угла падения и следовательно угол
меньше угла падения и следовательно угол 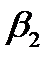 будет меньше угла
будет меньше угла 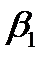 . Если
. Если 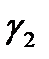 весьма мало, то угол
весьма мало, то угол 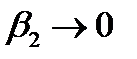
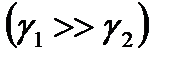
Лекция №6
Тема: Стационарное магнитное поле .
1. Источник магнитного поля. Магнитное поле постоянного тока – это одна из копонент электромагнитного поля, не изменяющегося во времени. Оно создается неизменными во времени токами, протекающими по проводящим телам, неподвижным в пространстве по отношению к наблюдателю. Хотя при протекании постоянных токов иметься и вторая компонента электромагнитного поля, а именно электрическое поле, оно во времени не меняется и поэтому не влияет на магнитное поле. Поэтому магнитное поле постоянного тока можно рассмотреть независимо от электрического.
- Основные величины, характеризующие магнитное поле.
Магнитная индукция 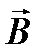 – векторная величина, определяемая по силовому воздействию магнитного поля на ток (
– векторная величина, определяемая по силовому воздействию магнитного поля на ток ( 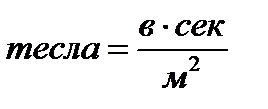 ).
).
Намагниченность 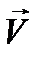 - магнитный момент единицы объема вещества [aмпep/м].
- магнитный момент единицы объема вещества [aмпep/м].
Напряжённость магнитного поля 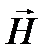 [ампер/м].
[ампер/м].
Намагниченность 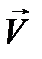 представляет собой вектор, направление которого совпадает с направлением напряженности
представляет собой вектор, направление которого совпадает с направлением напряженности 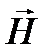 в данном токе;
в данном токе; 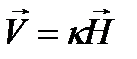
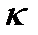 (каппа) (6.1)
(каппа) (6.1)
Коэффициент 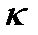 для ферромагнитных веществ является функцией Н.
для ферромагнитных веществ является функцией Н.
Три величины 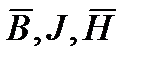 связаны соотношением:
связаны соотношением:
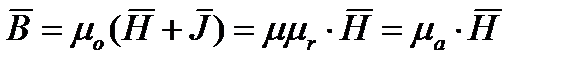
где 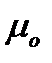 - магнитная постоянная в СИ [
- магнитная постоянная в СИ [ 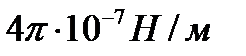 ] (6.2)
] (6.2)
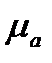 - абсолютная магнитная проницаемость;
- абсолютная магнитная проницаемость;
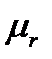 - относительная магнитная проницаемость
- относительная магнитная проницаемость
Подставив (6.1) в (6.2) и обозначив 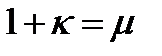 получим
получим 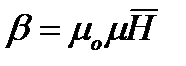
где 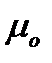 - постоянная, характеризующая магнитное свойство вакуума
- постоянная, характеризующая магнитное свойство вакуума
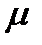 - относительная магнитная проницаемость.
- относительная магнитная проницаемость.
Магнитный поток Ф – есть поток вектора магнитной индукции 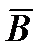 через площадь S:
через площадь S:
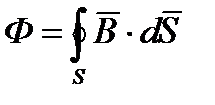
Где dS - элемент поверхности S, в СИ магнитный поток измеряется в веберах (Вб)или (в/сек).
При расчетах магнитных цепей обычно используются две величины: магнитную индукцию В и напряженность магнитного поля Н. Намагниченность V в расчетах, как правило не используется, но при необходимости V находится по формуле: 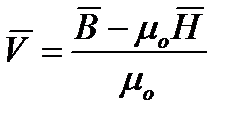
- Закон полного тока. Магнитное поле создается электрическими токами. Количественная связь между магнитным интегралом от вектора напряженности магнитного поля
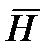 вдоль любого произвольного контура и алгебраической суммой токов
вдоль любого произвольного контура и алгебраической суммой токов 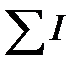 , охваченных этим контуром, определяется законом полного тока:
, охваченных этим контуром, определяется законом полного тока:
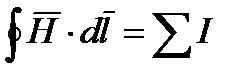 Н- вектор напряженности магнитного поля
Н- вектор напряженности магнитного поля
Положительное направление интегрирования 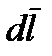 связано с положительным направлением тока I правилом правоходового винта. Закон полного тока является опытным законом. Его можно экспериментально проверить путем измерения
связано с положительным направлением тока I правилом правоходового винта. Закон полного тока является опытным законом. Его можно экспериментально проверить путем измерения 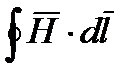 с помощью секционного устройства (известного из курса физики), называемого магнитным поясом.
с помощью секционного устройства (известного из курса физики), называемого магнитным поясом.
- Явление электромагнитной индукции.
 В первые обнаружено в 1831г английским физиком Майклом Фарадеем. Суть явления состоит в том, что при всяком изменении магнитного потока, пронизывающего какой-либо контур, независимо от того, чем вызвано изменение потока, в контуре находится электродвижущая сила e. Опыт показывает, что наведенная, или индуцированная Э.Д.С. прямо пропорциональна скорости изменения потокосцепления
В первые обнаружено в 1831г английским физиком Майклом Фарадеем. Суть явления состоит в том, что при всяком изменении магнитного потока, пронизывающего какой-либо контур, независимо от того, чем вызвано изменение потока, в контуре находится электродвижущая сила e. Опыт показывает, что наведенная, или индуцированная Э.Д.С. прямо пропорциональна скорости изменения потокосцепления 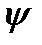 (пси)
(пси)
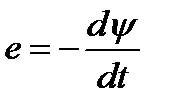 (7.3)
(7.3)
Потокосцепление контура 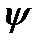 равно алгебраической сумме потоков, пронизывающих отдельные витки обмотки:
равно алгебраической сумме потоков, пронизывающих отдельные витки обмотки: 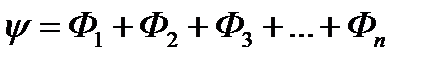
Если все витки обмотки 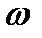 пронизываются одним и тем же потоком Ф , то
пронизываются одним и тем же потоком Ф , то 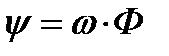
Так как число витков 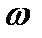 - величина безразмерная, то потокосцепление измеряют в тех же единицах, что и поток.
- величина безразмерная, то потокосцепление измеряют в тех же единицах, что и поток.
Сделаем важные заключения к формуле наведенной Э.Д.С.
1) 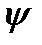 есть полное и результирующее потокосцепление контура или обмотки, оно создается не только внешним по отношению к данному контуру потоком, но и собственным потоком, пронизывающим контур при протекании по нему электрического тока.
есть полное и результирующее потокосцепление контура или обмотки, оно создается не только внешним по отношению к данному контуру потоком, но и собственным потоком, пронизывающим контур при протекании по нему электрического тока.
2) Знак (-) объясняется тем, что положительное направление отсчета для найденной Э.Д.С. и положительное направление линии магнитной индукции, пронизывающих контур при возрастании потока, принято связывать правилом правоходового винта. Если закручивать правоходовый винт, так, что его острие будет двигаться по направлению магнитных силовых линий при возрастании потока, то положительное направление для найденной Э.Д.С. будет совпадать с направлением вращения головки этого винта. Знак (-) в формулах (7.3) поставлен с целью приведения в соответствие действительных ( полученных из опыта) направлений Э.Д.С. при оговоренных условиях, принятых для нее за положительные.
Э.Д.С., наведенную в проводнике длиной dl, пересекающем магнитное поле определяется по формуле:
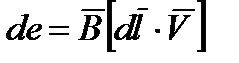 , где (7.4)
, где (7.4)
de - Э.Д.С. в участке проводника длиной dl,
V - скорость перемещения проводника относительно внешнего магнитного поля.
В формуле (7.4) индукция 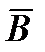 скалярно умножается на векторное произведение (
скалярно умножается на векторное произведение ( 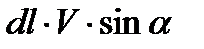 )
)
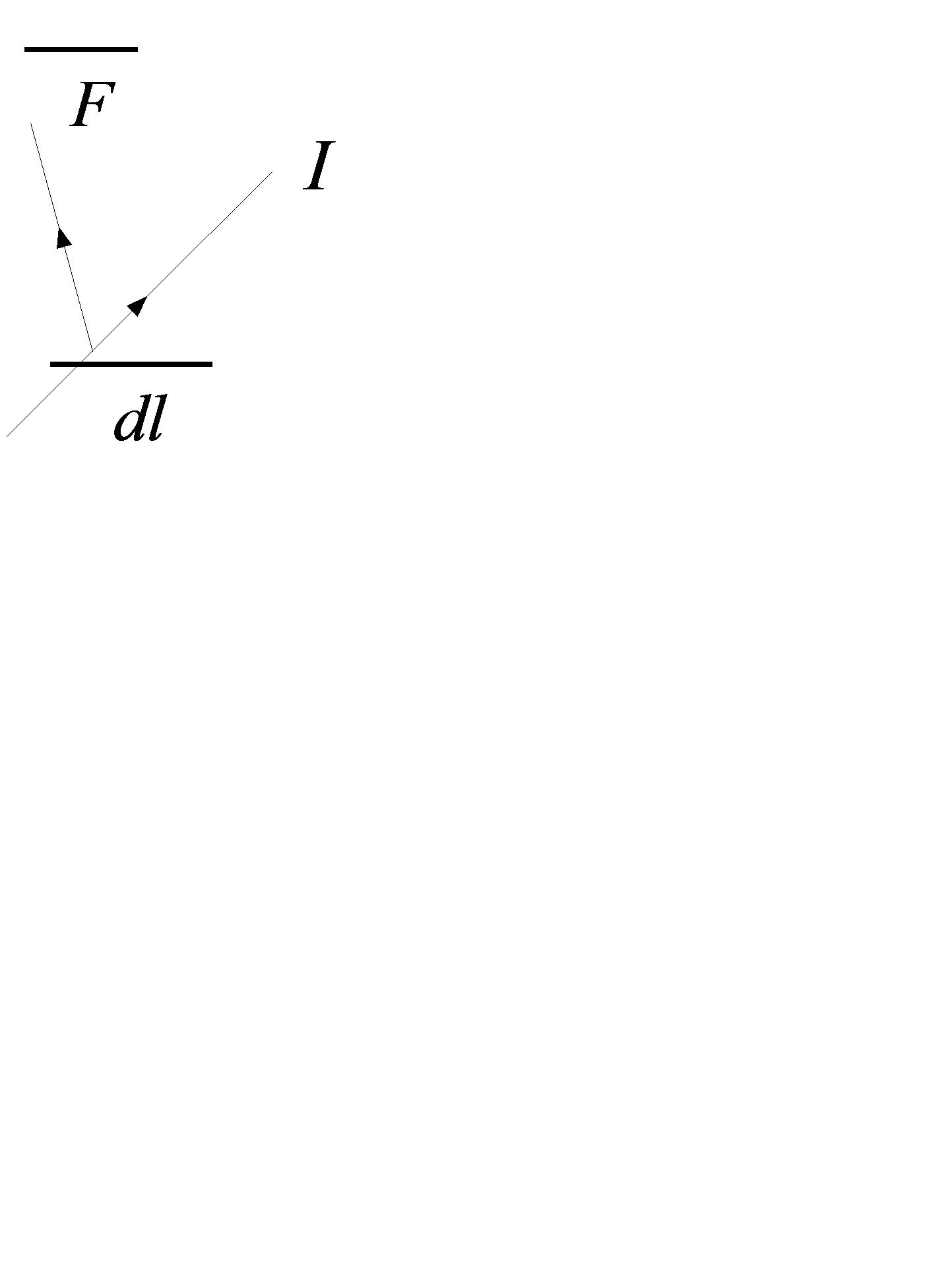
- Формула Ампера.
Одним из основных проявлений магнитного поля является воздействие его на проводник с током, помещенный в это поле. Опыт показывает, что сила 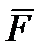 , с которой магнитное поле действует на элемент проводника длиной
, с которой магнитное поле действует на элемент проводника длиной 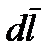 с током
с током 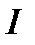 , определяется по формуле:
, определяется по формуле:
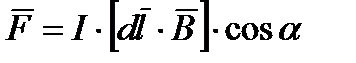 (7.5)
(7.5)
Эта сила называется силой Ампера и направлена перпендикулярно элементу тока 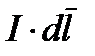 (рис.1).
(рис.1).



 Внешнее собственное
Внешнее собственное
однородное поле магнитное поле провода
Если индукция 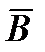 и элемент длиной dl параллельны, то элемент тока не испытывает механического воздействия со стороны магнитного поля. Воздействие на элемент тока максимально, когда
и элемент длиной dl параллельны, то элемент тока не испытывает механического воздействия со стороны магнитного поля. Воздействие на элемент тока максимально, когда 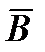 и dl взаимно перпендикулярны. Из (7.5) следует, что индукция
и dl взаимно перпендикулярны. Из (7.5) следует, что индукция 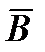 это силовая характеристика магнитного поля, определенная при условии, что внесенный в данную точку элемент тока
это силовая характеристика магнитного поля, определенная при условии, что внесенный в данную точку элемент тока 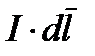 , расположенный перпендикулярно
, расположенный перпендикулярно 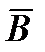 , не исказил магнитного поля, существовавшего до внесения в эту точку элемента тока. Другими словами, при оговоренном расположении элемента тока индукция численно определяется как:
, не исказил магнитного поля, существовавшего до внесения в эту точку элемента тока. Другими словами, при оговоренном расположении элемента тока индукция численно определяется как:
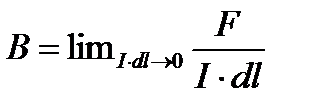
Имея в виду это условие, индукцию можно определить, как силу, действующую на проводник длинной dl, равной единице, если по нему протекает ток I, равный единице. Механическое воздействие магнитного поля на ток можно пояснить исходя из представлений о деформации силовых линий магнитного поля. Деформация силовых линий иллюстрируется рис.2 – 4. На рис. 2 изображены силовые линии равномерного магнитного поля, до внесения в него провода с током. На рис. 3 – силовые линии провода с током. На рис. 4 – силовые линии результирующего поля. Слева от провода силовые линии собственного поля провода направлены встречно силовым линиям внешнего равномерного поля, и с права согласно им. По этому результирующее поле слева от провода разрежено, а с права сгущено. Силовые линии, стремясь выпрямиться, производят давление на провод справа налево.
При взаимно перпендикулярном расположении линии магнитного поля и провода с током направление действия силы по мнемоническому правилу, получившему название левой руки. Если расположить левую руку таким образом, что силовые линии будут входить в ладонь, вытянутые пальцу направить по току, то отогнутый большой палец покажет направление действующей силы. Взаимодействие магнитного поля с током имеет место независимо от причин возникновения магнитного поля. В результате ли протекания макро токов в электрических контурах или вследствие протекания микро токов ферромагнитных материалах.
Рассмотрим пример взаимодействия двух параллельных проводников с током 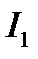 и
и 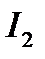 .
.
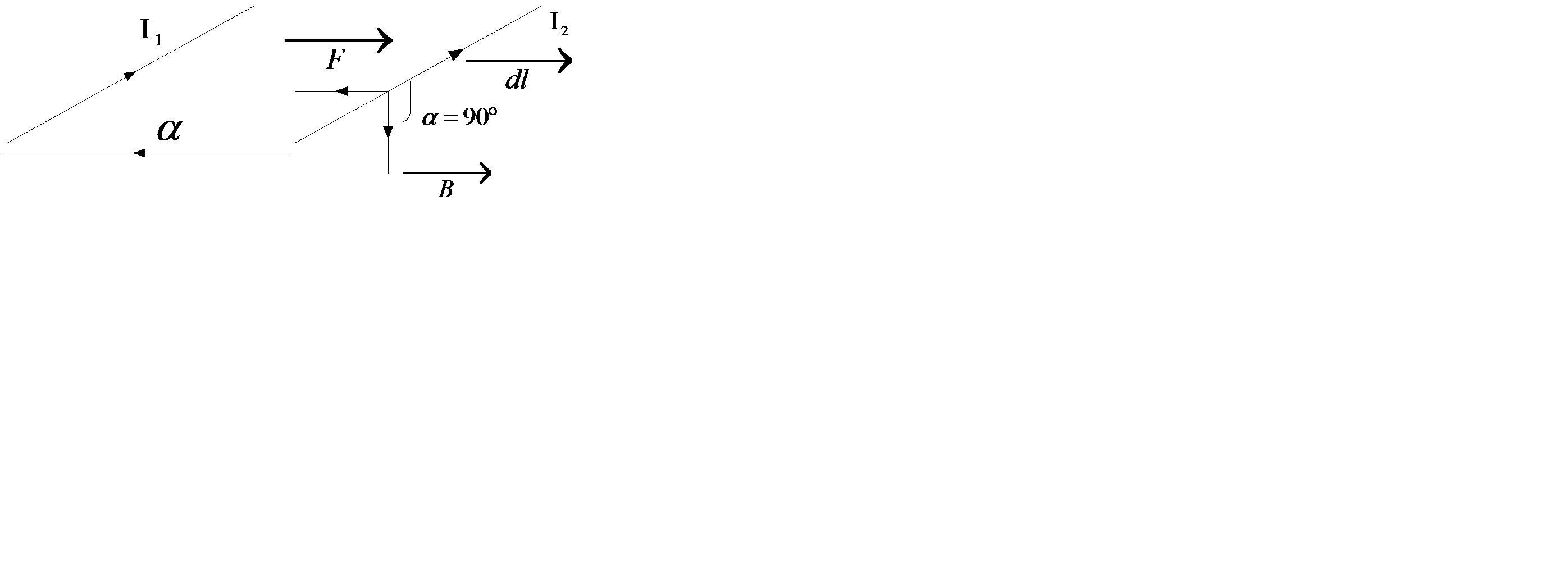
По первому проводу течет ток  , по второму
, по второму 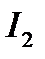 . Воспользуемся формулой Ампера
. Воспользуемся формулой Ампера
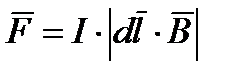
Учтем, что угол между элементом длины второго провода dl индукции 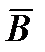 от левого провода равен
от левого провода равен 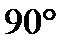 . По этому модуль векторного произведения
. По этому модуль векторного произведения 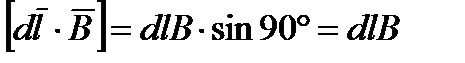
Магнитная индукция, создаваемая первым проводом, где расположен второй провод по закону полного тока
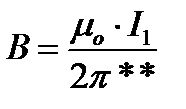
Сила Ампера будет
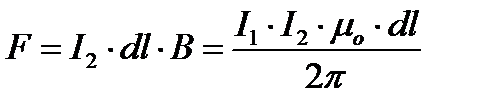
Под действием силы провода стремятся сблизится.
- Принцип непрерывности магнитного потока и запись в дифференциальной форме.
Магнитный поток есть поток вектора магнитной индукции через некоторую поверхность:
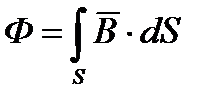
Индекс S под знаком интеграла свидетельствует о том, что интеграл взят по поверхности S.
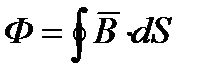
Опыт показывает, что вошедший внутрь любого объема магнитный поток равен магнитному потоку вышедшему из того же объема. Следовательно, алгебраическая сумма вошедшего в объем и вышедшего из объема потоков равна нулю:
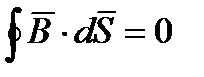 (6.5)
(6.5)
Выражение (6.5) представляет собой математическую запись принципа непрерывности магнитного потока.
Разделим обе части (6.5) на объем V, находящейся внутри замкнутой поверхности S, и найдем предел отношения когда объем 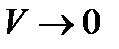 .
.
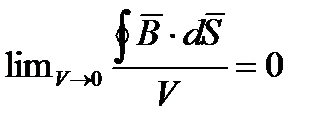 или
или 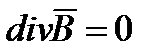 (6.6)
(6.6)
Выражение (6.6) трактуется как дифференциальная форма принципа непрерывности магнитного потока. Оно пригодно для любой точки магнитного поля. Следовательно, в любой точке этого поля нет ни истока, ни стока линии вектора магнитной индукции. Линии вектора 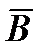 ни где не прерываются, они представляют собой замкнутые сами на себе линии (окружность – пример замкнутой на себе линии). Но линии
ни где не прерываются, они представляют собой замкнутые сами на себе линии (окружность – пример замкнутой на себе линии). Но линии 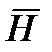 в точках, где изменяется вектор намагниченности V (например на границах сред с разными
в точках, где изменяется вектор намагниченности V (например на границах сред с разными 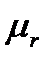 ) прерывен. Это следует из (6.6).
) прерывен. Это следует из (6.6).
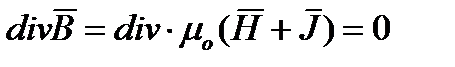
отсюда 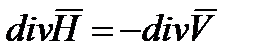
С другой стороны в электрическом поле существует прерывность линий вектора напряженности 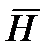 и непрерывность вектора электрического смещения
и непрерывность вектора электрического смещения 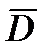 ,
,
Дата добавления: 2015-12-16; просмотров: 5746;
