Уравнение Максвелла. Полная система уравнений электромагнитного поля.

Ток смещения.

Максвеллом была выдвинута гипотеза о симметрии во взаимодействии и взаимозависимости электрического и магнитного полей. Если изменяющееся во времени магнитное поле 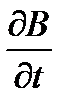создает электрическое поле, следует ожидать, что изменяющееся во времени электрическое поле 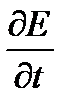создает магнитное поле. То есть имеет место индукция магнитного поля электрическим. Докажем возможность существования этого нового явления индукции. Согласно теореме о циркуляции вектора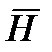

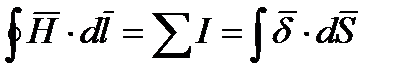
Применим эту теорему к случаю, когда предварительно заряженный плоский конденсатор разряжается через некоторое внешнее сопротивление

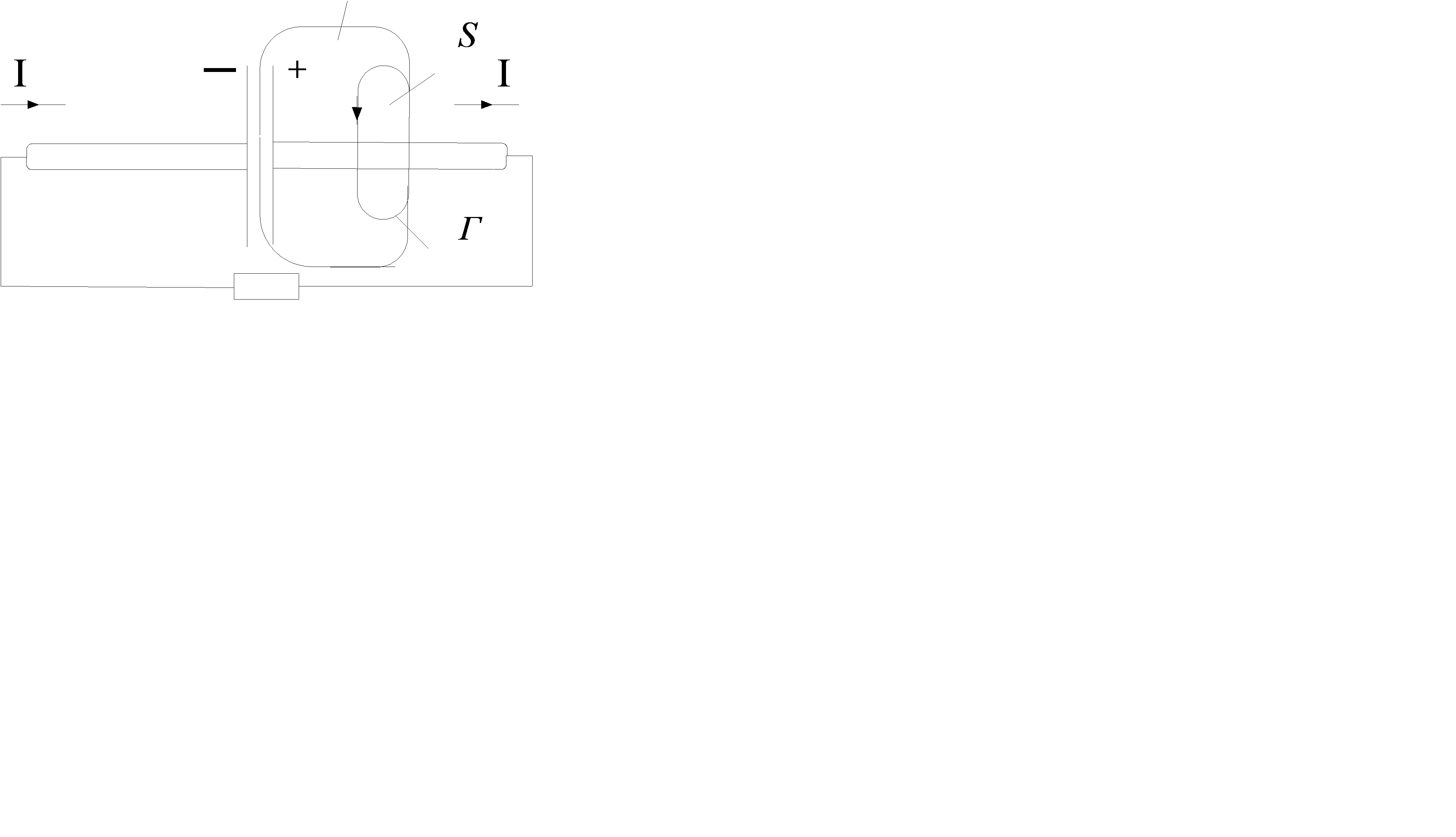
В качестве контура Г возьмем кривую охватывающую провод. На контур Г можно наложить разные поверхности, например S и 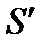. Обе поверхности с точки зрения математики должны быть равноценны, однако на практике через поверхность S течет ток I, а через поверхность 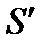ток не течет. Таким образом получается с физической точки зрения парадоксальная и противоречивое явление, что циркуляция вектора 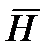зависит от вида поверхности налагаемой на выбранный контур циркуляции или обхода. Разрешим это противоречие путем следующих рассуждений: поверхность 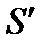пронизывает только электрическое поле. По теореме Гаусса поток вектора электрического смещения 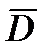сквозь замкнутую поверхность определяется как

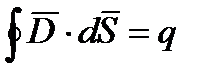, откуда

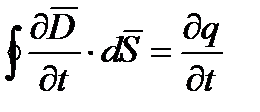(10.1)

С другой стороны, согласно уравнению непрерывности электрического тока. выражающего закон сохранения электрического заряда,

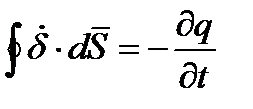(10.2)

Ток, протекающий через замкнутую поверхность S, численно равен убыли заряда в единицу времени, внутри объема V, находящегося внутри этого замкнутой поверхности. В случае стационарного (постоянного тока) распределение зарядов в пространстве остается неизменным, т. е. 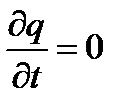, и для постоянного тока

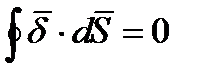(10.3)

Сложив, отдельно левые и правые части уравнений (10.1) и (10.2) получим

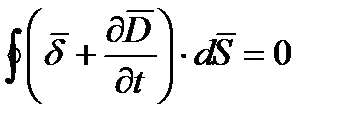(10.4)

Это уравнение аналогично уравнению непрерывности для постоянного тока. Из него видно, что кроме вектора плотности тока проводимости 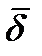имеется еще одно слагаемое 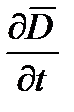, размерность которого равна размерности плотности тока. Максвелл назвал это слагаемое плотностью тока смещения.

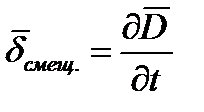
Сумму тока проводимости и тока смещения называют полным током, с плотностью

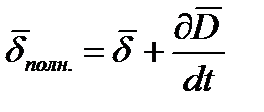
Согласно (10.4) линии полного тока являются непрерывными в отличии от линии тока проводимости. Токи проводимости, если они не замкнуты, замыкаются токами смещения.

Убедимся, что введение понятия полного тока разрешает противоречие, обусловленное зависимостью циркуляции вектора 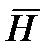от выбранной поверхности, налагаемой на контур Г. Для этого достаточно в уравнении циркуляции вектора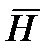

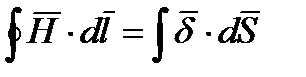
вместо тока проводимости 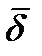ввести полный ток, то есть величину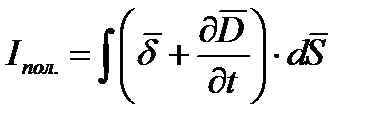

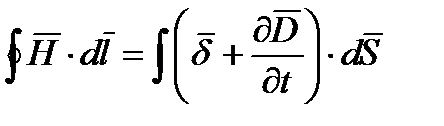
Покажем, что полный ток 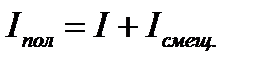будет одинаков и для поверхности S и поверхности 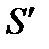, помещенных на контур Г. Для этого применим уравнение (10.4) к замкнутой поверхности, составленной из поверхностей S и .

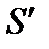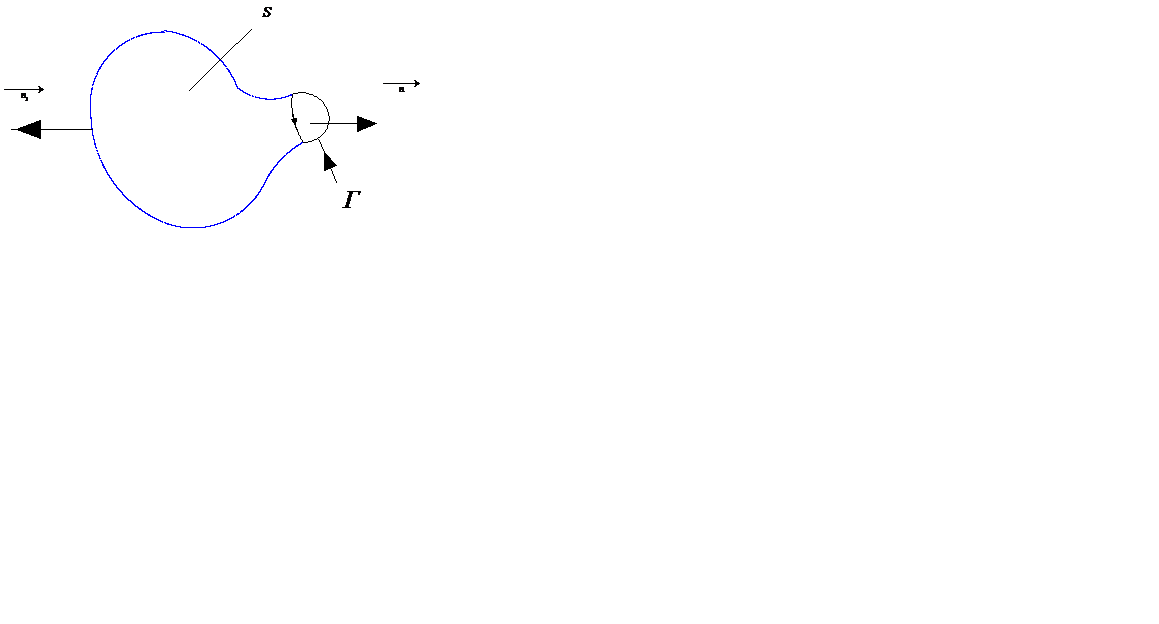
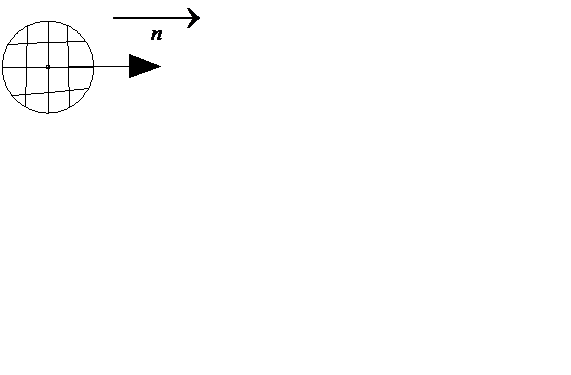
Учитывая, что для замкнутой поверхности нормаль 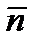направлена наружу, запишем

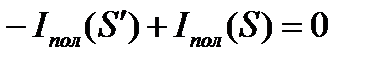
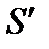Теперь если перевернуть нормаль для поверхности в туже сторону, что и для S, то

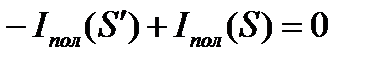и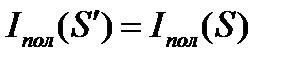

Таким образом теорема о циркуляции вектора 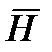в общем виде для произвольного случая записывается как

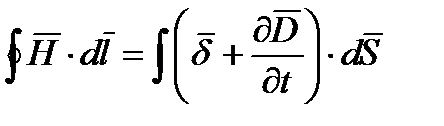(10.5)

Дифференциальная формула записи уравнения циркуляции вектора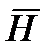

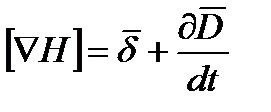
Векторное произведение оператора Гамильтона на 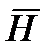(или ротор вектора 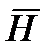) определяется плотностью тока проводимости 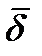и тока смещения 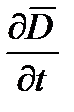в этой же точке.