Количественные показатели безотказности

Наиболее важные показатели надежности невосстанавливаемых объектов – показатели безотказности, к которым относятся:

· вероятность безотказной работы;

· плотность распределения отказов;

· интенсивность отказов;

· средняя наработка до отказа.

Показатели надежности представляются в двух формах (определениях):

- статистическая (выборочные оценки);

- вероятностная.

Статистические определения (выборочные оценки) показателей получаются по результатам испытаний на надежность.

Допустим, что в ходе испытаний какого-то числа однотипных объектов получено конечное число интересующего нас параметра – наработки до отказа. Полученные числа представляют собой выборку некоего объема из общей «генеральной совокупности», имеющей неограниченный объем данных о наработке до отказа объекта.

Количественные показатели, определенные для «генеральной совокупности», являются истинными (вероятностными) показателями, поскольку объективно характеризуют случайную величину – наработку до отказа.

Показатели, определенные для выборки, и, позволяющие сделать какие-то выводы о случайной величине, являются выборочными (статистическими) оценками. Очевидно, что при достаточно большом числе испытаний (большой выборке) оценки приближаются к вероятностным показателям.

Вероятностная форма представления показателей удобна при аналитических расчетах, а статистическая – при экспериментальном исследовании надежности.

Для обозначения статистических оценок будем использовать знак сверху.

Примем следующую схему испытаний для оценки надежности.

Пусть на испытания поставлено N одинаковых серийных объектов. Условия испытаний идентичны, а испытания каждого из объектов проводятся до его отказа.

Введем следующие обозначения:

T = {0, t₁, … t_N } = {t} – случайная величина наработки объекта до отказа;

N(t) – число объектов, работоспособных к моменту наработки t;

n(t) – число объектов, отказавших к моменту наработки t;

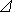n(t, t + 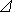t) – число объектов, отказавших в интервале наработки [t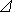, t + t];

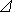t – длительность интервала наработки.

Поскольку в дальнейшем определение выборочных оценок базируется на математических моделях теории вероятностей и математической статистики, то ниже приводятся основные (минимально необходимые) сведения из теории вероятностей.

Более подробный материал из теории вероятностей читатель может получить в Приложении: «Основные понятия и краткие сведения из теории вероятностей».