Модельные представления об электропроводности кристаллов
Пусть единице объема кристаллов имеется n свободных электронов. Назовем среднюю дрейфовую скорость электронов 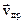 по определению:
по определению:
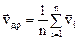 (10)
(10)
В отсутствии внешнего поля 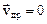 и электрический ток в кристалле отсутствует. При наложении на кристалл внешнего электрического поля
и электрический ток в кристалле отсутствует. При наложении на кристалл внешнего электрического поля 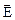 в кристалле возникает ток(
в кристалле возникает ток( 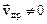 ). Согласно закону Ома
). Согласно закону Ома 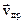 конечна и притом, пропорциональна силе
конечна и притом, пропорциональна силе 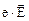 .
.
Из механики известно, что если скорость установившегося движения пропорциональна внешней приложенной силе F то кроме силы F на тело действует сила сопротивления среды, которая пропорциональна скорости тела, то есть на электрон действует сила «трения» по закону:
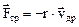 , (11)
, (11)
где r– коэффициент пропорциональности. Для «среднего» электрона уравнение движения приобретает вид
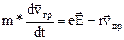 , (12)
, (12)
где m* – эффективная масса электрона.
После установления стационарного состояния выключим поле 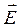 получим уравнение:
получим уравнение:
 . (13)
. (13)
Его решение имеет вид:
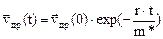 (14)
(14)
где 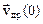 значение дрейфовой скорости в момент включения поля. Откуда следует, что за время t=m*/r дрейфовая скорость уменьшается в e раз. В результате имеем
значение дрейфовой скорости в момент включения поля. Откуда следует, что за время t=m*/r дрейфовая скорость уменьшается в e раз. В результате имеем
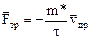 . (15)
. (15)
Установившееся значение дрейфовой скорости можно найти, считая, что  , тогда
, тогда
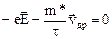
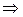
 (16)
(16)
Отсюда можно получить установившееся значение плотности тока, умножив 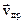 на -е и концентрацию электронов n:
на -е и концентрацию электронов n:
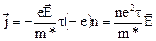 (17)
(17)
где коэффициент  – удельная электропроводность.
– удельная электропроводность.
Введем такую физическую величину как подвижность свободных носителей заряда m
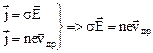 . (18)
. (18)
Откуда
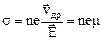 , (19)
, (19)
где  – подвижность носителей тока.
– подвижность носителей тока.
Для собственных полупроводников носителями тока являются одновременно электроны и дырки:
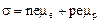 , (20)
, (20)
где
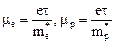 . (21)
. (21)
Можно сказать про понятие времени t то, что величина t=m*/r представляет собой время релаксации, характеризующее процесс установления равновесия между электроном и решеткой, нарушенного действием внешнего поля 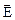 .
.
Дата добавления: 2015-12-16; просмотров: 776;
