Элементарная теория эффекта Холла

Если полупроводник, по которому протекает электрический ток, поместить в магнитное поле, то в нем возникает ряд эффектов. Физические явления, возникающие в веществе, находящемся в магнитном поле, при прохождении через него электрического тока, называются гальваномагнитными явлениями (эффектами). К гальваномагнитным явлениям относят эффект Холла и магнетосопротивление.

Эффект Холла в полупроводниках – это появление поперечной разности потенциалов в полупроводниковом образце с током, помещенном в магнитное поле. Если пластинку из полупроводника с одним типом носителей заряда, например, с электронами, поместить во внешнее поперечное магнитное поле индукцией 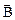(рис.1а) и пропустить вдоль нее ток I₁₂, то под действием силы Лоренца вследствие смещения движущихся носителей заряда (электронов) к одной из граней пластинки возникает ЭДС Холла. На рис.1 направление дрейфовой скорости электронов (или дырок) 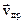показано стрелкой. Магнитное поле перпендикулярно плоскости рисунка.

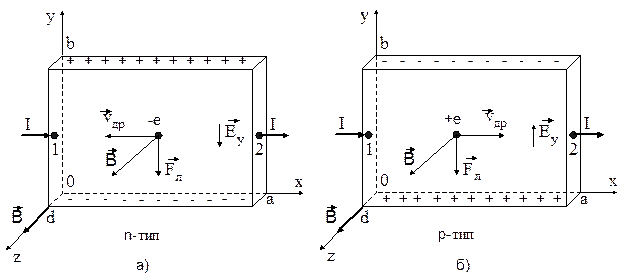
Рис. 1

На рис.1а под действием силы Лоренца электроны будут отклоняться к нижней грани образца, на которой скапливается отрицательный заряд; на противоположной верхней грани остается нескомпенсированный положительный заряд кристаллической решетки. Возникающая вследствие этого между верхней и нижней гранями поперечная разность потенциалов называется электродвижущей силой Холла.

Получим формулу для эдс Холла. Накопление заряда на боковых гранях образца будет продолжаться до тех пор, пока поперечное электрическое поле Холла 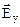не уравновесит силу Лоренца

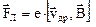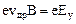; => . (22)

Отсюда находим напряженность 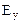поперечного холловского поля

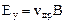. (23)

Неизвестную дрейфовую скорость носителей можно выразить через силу тока I (или плотность тока )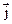

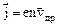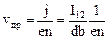=> , (24)

где n - концентрация носителей тока в образце; d, b - толщина и ширина образца. Подставляя (24) в (23), получаем

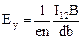. (25)

Эдс Холла равна разности потенциалов между верхней и нижней гранями

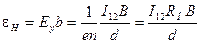, (26)

где

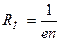– коэффициент Холла. (27)

Для полупроводника р- типа можно получить то же выражение, только концентрация электронов n будет заменена концентрацией дырок р, а направление холловского поля будет противоположным (рис.1б) (убедиться в этом самостоятельно).

Значение коэффициента Холла R, входящее в выражение (27), справедливо только для вырожденных полупроводников или металлов, когда можно не учитывать распределение электронов по скоростям, что и допускалось при выводе. Более точное значение коэффициента Холла отличается от имеющегося в выражении (27) множителем А. Для полупроводников различных типов (с атомной, ионной решетками) А изменяется в зависимости от механизма рассеяния при различных температурах примерно от 1 до 2 (например, для образца в данной работе ( )).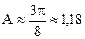

Таким образом, для полупроводника n – типа

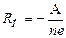. (28)

Для полупроводника р -типа

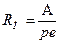. (29)

Знак минус в формуле (28) означает, что эдс Холла для полупроводника n - типа имеет полярность, противоположную полярности для полупроводника р - типа.

Из анализа выражений (26), (27) видно, что значения эдс Холла 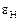, индукции 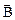, силы тока I₁₂ позволяют вычислить коэффициент Холла R, что в свою очередь позволяет определить по формулам (28), (29) концентрацию и знак носителей заряда в образце. Удельное сопротивление 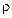полупроводника, из которого изготовлен образец, можно вычислить по обычной формуле

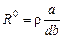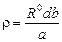® , (30)

где R⁰ - сопротивление образца без магнитного поля (между контактами 1, 2), 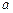– длина образца.

Электрические свойства полупроводника характеризуются не только концентрацией n носителей, но и их подвижностью 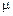. Подвижность носителей тока - это отношение дрейфовой скорости носителей к напряженности внешнего электрического поля

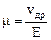. (31)

Следовательно, подвижность характеризует дрейфовую скорость носителей тока при напряженности внешнего поля, равной единице. Подвижность носителей тока определяет величину электропроводности полупроводника так же, как и концентрация носителей тока. Материалы с большой подвижностью носителей тока имеют меньше удельное сопротивление и соответственно большую электропроводность 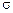. Это видно из следующих формул:

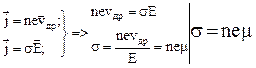. (32)

Если помимо эдс Холла измерить электропроводность 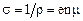, то можно найти подвижность электронов (или дырок):

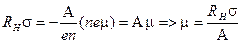. (33)

Таким образом, по измерению эдс Холла и проводимости можно определить такие важные характеристические параметры полупроводника, как знак и концентрацию основных носителей заряда и их подвижность.