Эффективная масса свободных носителей заряда в кристаллах

ОПРЕДЕЛЕНИЕ КОНЦЕНТРАЦИИ И ПОДВИЖНОСТИ НОСИТЕЛЕЙ ЗАРЯДА

В ПОЛУПРОВОДНИКАХ ПУТЕМ ИЗМЕРЕНИЯ Коэффициента ХОЛЛА

Эффективная масса свободных носителей заряда в кристаллах

Движение электронов в кристалле под действием внешнего электрического поля Е сильно отличается от движения свободного электрона. Дело в том, что в кристалле на электрон помимо внешнего поля действуют силы со стороны кристаллической решетки. Однако для описания поведения электрона кристалла во внешнем поле уравнения движение электрона удобно представить в том же виде, что и для движения свободного электрона, то есть в виде 2-го закона Ньютона относительно внешней силы.

Скорость электрона в кристалле может быть представлена как групповая скорость волнового пакета v_гр

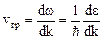(1)

Работа сил на участке 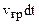равна

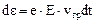(2)

Подставив (1) в правую часть (2) , получим:

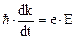(3)

Продифференцировав (1) по времени получим:

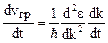(4)

Заменим в (4) dk/dt из (3) на 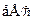и получим:

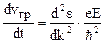; (5)

в последнем равенстве сделаем обозначение:

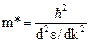(6)

и F=eE. Получим

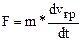, (7)

где m* эффективная масса. В итоге получаем уравнение движения электрона в форме 2-го закона Ньютона. Если в кристалле известна зависимость 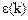, то можно вычислить m* или, по крайней мере, оценить характер ее изменения при движении в разрешенной энергетической зоне. Эффективная масса есть мера взаимодействия электрона с решеткой, а не мера инертных и гравитационных свойств. В общем случае m* – это тензор, элементы которого соответственно равны

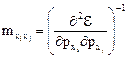. (8)

Для свободного электрона, на который не действуют силы со стороны решетки, получаем

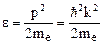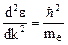=> => m*=m_е , (9)

то есть эффективная масса равна обычной.

Введя понятие эффективной массы, можно считать электрон свободным и описывать его движение по тем же формулам, что и для свободного электрона , не учитывая влияние периодического поля кристалла.