Общий вид формулы для функции распределения
Вероятность того , что скоростная точка молекулы окажется в элементе dw:
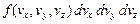 . (2)
. (2)
Это значит, что компонента скорости vx должна попасть в интервал vx, vx+dvx. Назовём это событием А. Аналогично vy должна попасть в интервал vy, vy+dvy, что назовём событием В. И наконец vz, должна попасть в интервал vz, vz+dvz. Это событие С.
По предположению Максвелла события А, В, С независимы. Тогда попадание скоростной точки dw есть сложное событие, являющееся произведением событий А, В, С. Применим теорему об умножении вероятностей.
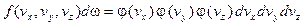 . (3)
. (3)
Здесь j (vx)dvx – вероятность того, что компонента скорости vx лежит в интервале dvx. Аналогично определены j (vy) и j (vz). Это одномерные функции распределения.
1.3. Определение вида одномерных функций распределения
В состоянии равновесия положительные и отрицательные направления скоростей молекул газа равновероятны. Отсюда следует
j (vx) = j (-vx). (4)
Отсюда можно предположить, что функции j зависят от квадрата компонент скорости v2x, v2y, v2z. Вместо квадратов скоростей удобнее взять в качестве аргументов соответствующие кинетические энергии
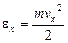 ;
; 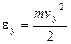 ;
; 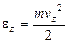 ; (5)
; (5)
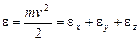 . (6)
. (6)
С учетом этого трехмерная функция распределения запишется в виде
j (ex) j (ey) j (ez) = j (ex+ ey+ ez)= j (e). (7)
1.4. Функциональное уравнение для определенияj (e) и его решение
Рассмотрим двумерное движение. Из закона сохранения энергии ex+ ey = const. Если e = const, то вероятность j (e) = const. Получаем функциональное уравнение для определения j :
j (ex) j (ey) = const. (8)
ex + ey = const. (9)
Решение данного уравнения – дело математической техники. Вначале сведём два равенства в одно дифференциальное уравнение. Логарифмируем (8)
lnj (ex) + ln j (ey) = const. (10)
Дифференцируем (9) и (10)
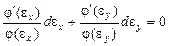 . (11)
. (11)
dex+ dey=0. (12)
Объединяя (11) и (12), получаем
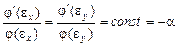 . (13)
. (13)
Решаем уравнение для j (ex):
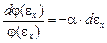 ; (14)
; (14)
lnj = -a ex+const. (15)
Отсюда имеем общий вид одномерных функций распределения
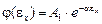 ;
; 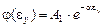 ;
; 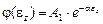 (16)
(16)
и общий вид трехмерной функции распределения
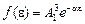 . (17)
. (17)
1.5. Определение постоянной А1 из условия нормировки
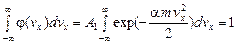 . (18)
. (18)
Интегрируем методом замены переменной: 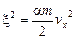 . (19)
. (19)
Интеграл Пуассона: 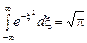 . (20)
. (20)
Окончательно получаем 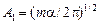 . (21)
. (21)
Дата добавления: 2015-12-16; просмотров: 791;
