Теория метода исследования

В замкнутом сосуде, наполненном газом, при температуре Т устанавливается термодинамическое равновесие, которое характеризуется определённым распределением молекул по скоростям. Среднее число молекул в единице объёма 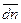, скорость которых заключена между v и v + dv, равно произведению средней концентрации молекул идеального газа 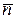на вероятность dP(v) того, что скорость молекулы лежит в интервале v и v + dv:

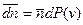. (27)

В зависимости от выбранной системы координат функция имеет разный вид. В декартовой системе:

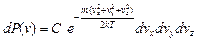; (28)

в цилиндрической системе:

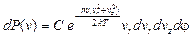; (29)

в сферической системе:

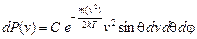, (30)

Здесь С – нормировочная константа, остальные обозначения являются общепринятыми.

Интегрируя (30) по всем возможным значениям углов j и q, можно найти вероятность dP(v) того, что молекула имеет скорость в интервале от v до v + dv:

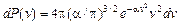, (31)

где a=m/2kT.

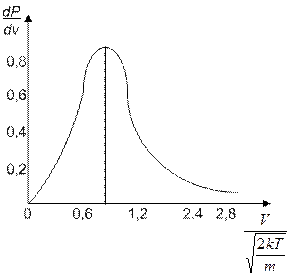
Рис. 4.

Функция 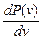обращается в нуль при v=0 и v=¥, имеет максимум при

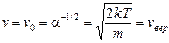. (32)

График функции изображен на рисунке 4.

Экспериментальная проверка распределения молекул по скоростям является одной из важнейших задач молекулярной физики. Существует несколько методов, прямых и косвенных, доказывающих справедливость этого закона. В работе для исследования вида функции распределения по скоростям предлагается метод задерживающего потенциала.

Суть метода состоит в следующем. Известно, что электронный газ, который образуется в пространстве между катодом и управляющей сеткой электронной лампы вследствие термоэлектронной эмиссии, подчиняется статистике Максвелла. Электронный газ имеет температуру катода. В многоэлектродной лампе типа пентода электронное облако из-за конструктивных особенностей лампы обладает осевой симметрией (катод представляет собой тонкий нагретый цилиндр). Для описания статистических свойств электронного газа в этом случае удобно применять формулу (29).

Если электроны, вылетающие из облака, заставить проходить через задерживающее радиальное электрическое поле, то при некоторой разности потенциалов U_з преодолеть влияние поля могут только те электроны, у которых радиальная составляющая скорости удовлетворяет условию

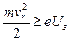, (33)

где e – заряд электрона, v_r – радиальная составляющая скорости электрона.

Определим число электронов, пролетающих через тормозящее поле в единицу времени, т.е. возникающий ток.

Сначала, пользуясь формулами (27) и (29), определим число электронов, имеющих значение радиальной составляющей скорости в интервале от v_r до v_r + dv_r. Интегрируя (27) с учетом выражения (29) по азимутальному углу в пределах от 0 до 2p и по компоненте скорости от - ∞ до + ∞, получим:

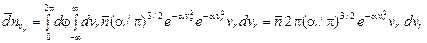. (34)

Число электронов 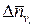, проходящих через поверхность цилиндрического электрода в единицу времени, равно 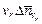, т.е.

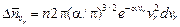. (35)

Наконец, число электронов 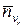, пролетающих в единицу времени через пространство с запирающим потенциалом U_з, определяется общим числом электронов, скорости которых превышают :

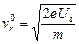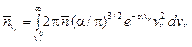. (36)

Из (36) видно, что общее число электронов, пролетающих в единицу времени через тормозящее поле, равно интегралу с переменным нижнем пределом от выражения, совпадающего с точностью до постоянной, с распределением Максвелла (31).

Меняя значение задерживающей разности потенциалов, можно получить функцию 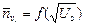, производная которой по 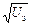представляет собой распределение Максвелла по скоростям.