С учётом (2.30) из зависимости (2.28) можно получить следующее

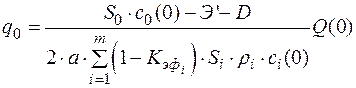. (2.31)

Найдём из последней зависимости константу D.

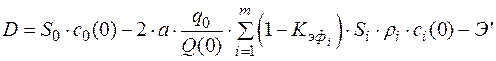. (2.32)

Подставляя найденное выражение для D, имеем окончательный вид зависимости для нахождения оптимального режима эксплуатации водозабора в принятых условиях и предположениях

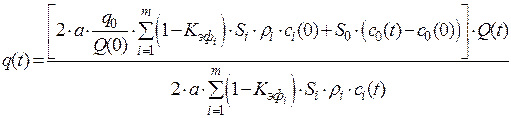. (2.33)

С учётом принятого начала отсчёта 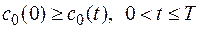, 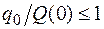и, следовательно, можно заключить, что числитель у дроби (2.33) меньше знаменателя для любого 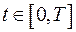. Из этого вытекает выполнение условий (2.22) и (2.23).

Таким образом, функция (2.33) оптимизирует забор воды из источника водоснабжения, максимизируя суммарный эффект от водопотребления и сохранности молоди рыб. Как видно, оптимальный режим водозабора существенно зависит от функций неравномерности получения эффекта от водоснабжения 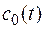и неравномерности ската молоди рыб .

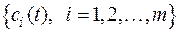В случае применения формулы (2.33) для нахождения оптимального режима эксплуатации водозабора в течение суток при 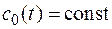, данная зависимость упрощается. Этот упрощённый вид также может использоваться для определения оптимального режима притока при расчёте ёмкости бассейна суточного регулирования.

Так как эффект от водоснабжения в течение суток может быть принят равномерным, т.е. 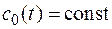, тогда оптимальный суточный режим забора воды из реки будет определяться по следующей зависимости

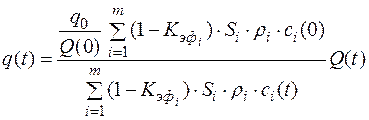. (2.34)

В течение рассматриваемого периода времени, для которого определяется режим водозабора, расход водоисточника может считаться постоянным, т.е. .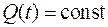

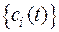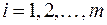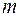Таким образом, имеем, что оптимальный расход водозабора в течение суток будет определяться только функциями неравномерности ската молоди рыб , , где − число учитываемых видоразмеров.