Стоимостное выражение ущерба рыбному хозяйству от водозабора определяется по зависимости (2.13).

Для определения эффекта от водоснабжения, получаемого за период времени 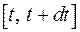, может быть применена следующая зависимость

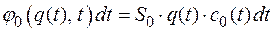, (2.18)

где 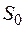– эффект от использования 1 м³ воды, забираемой из водотока
(брутто);

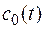− коэффициент неравномерности получения эффекта во времени.

Функция 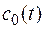отражает влияние подачи воды в разное времясуток. Величина 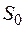может быть представлена в виде

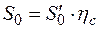, (2.19)

где 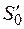– эффект от использования единицы водного ресурса, поданного на водоснабжение населения;

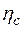− коэффициентполезного действия (КПД) системы.

Функцию эксплуатационных затрат представим в виде суммы неко­торой постоянной величины 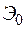, определяемой 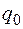, и изменяемой части, пропорциональной расходу воды в водозаборном сооружений

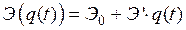, (2.20)

где 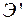− удельные эксплуатационные затраты.

С учётом полученных зависимостей математическая модель оптими­зации забора из источника водоснабжения будет иметь вид

найти такую 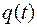, чтобы

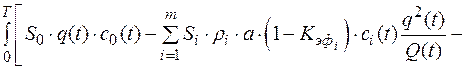
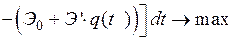, (2.21)

при ограничениях

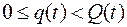; (2.22)

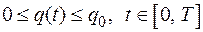. (2.23)

Рассмотрим вопросы определения оптимального режима .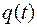

Вначале рассмотрим задачу (2.21) без ограничений (2.22) и (2.23).

В этом случае имеем классическую задачу вариационного исчисления без граничных условий 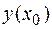, 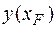вида (Г. Корн, 1973)

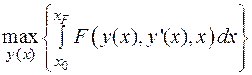, (2.24)

где ;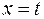

;

,

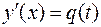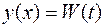где 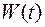− объём воды, прошедший в створе наблюдения.

Как видно из (2.21) подынтегральная функция в данном случае не зависит явно от функции 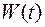, то есть

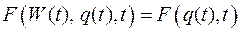. (2.25)

В этом случае функция 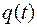ищется из решения упрощённого уравнения Эйлера (Г. Корн, 1973)

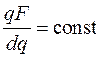. (2.26)

Найдём производнуюот подынтегральной функции функционала (2.25) и, приравняв её к некоторой константе D, имеем

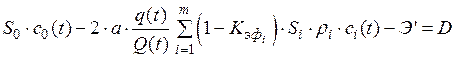. (2.27)

Разрешим (2.27) относительно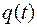

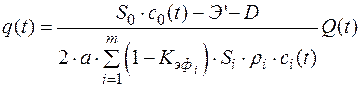. (2.28)

Анализ последней зависимости позволяет сделать вывод о том, что максимальный расход водозабор должен иметь в периоды наибольшего водопотребления и минимального ската молоди рыб в водотоке.

Момент времени, соответствующий максимально возможному расходу, обозначим через 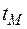. Эффективность максимального водозабора можно оценить с помощью следующей функции

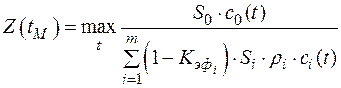. (2.29)

Момент 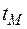примем за начало отсчёта рассматриваемого временного интервала, то есть 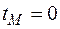. Тогда с учётом введённого в (2.9) смысла величины 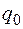можно принять

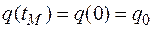. (2.30)