Моделирование камер локальной водохозяйственной системы для рыбоохранных целей

Для каждого типа камеры можно предложить зависимости, связывающие интенсивность ската молоди рыб (определённого вида и конкретной размерной группы) во входном и выходном створах камеры.

За характеристику ската молоди в некоторой камере будем принимать интенсивность ската в замыкающем (выходном) створе камеры. Очевидно, что это же значение будет характеризовать интенсивность ската во входном створе следующей (по течению реки) камеры.

Под интенсивностью ската молоди рыб 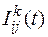будем понимать количество скатывающейся молоди i-го вида j-ой размерной группы через k-ый створ водотока за единицу времени.

Для I типа камеры (участок реки без притоков и рукавов) характерно незначительное изменение общего количества скатывающейся молоди, которая возможно только за счёт естественной гибели молоди и попадания в малые водозаборы из-за не стопроцентной эффективности их рыбозащитных устройств. В случае необходимости гибель молоди можно учесть с помощью коэффициента выживаемости молоди на данном участке водотока. Схема камеры первого типа и соответствующий граф связи приведены на рисунке 3.4.

а − схема k-ой камеры; б − граф связи для k-ой камеры

Рисунок 3.4 − Формализация камеры I типа

Таким образом, k-ая камера ограничена (k-1)-ым и k-ым створами реки. Причём согласно камерной модели, описанной в разделе 3.2, интенсивности ската молоди всех рассматриваемых видов и размерных групп в (k-1)-ом створе являются известными. Если скат молоди в k-ой камере происходит за время 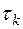, то для камеры I типа можно записать следующее общее отношение

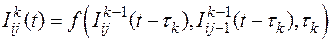. (3.1)

Конкретизация данной зависимости возможна на базе статистических или аналитических моделей.

В первом случае, если протяжённость участка такова, что молодь из
(j-1) размерной группы переходит только в j-ую размерную группу, на основе статистических данных определяется регрессионная зависимость вида

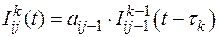, (3.2)

где 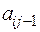− эмпирический коэффициент линейной регрессии.

Такого типа зависимости для некоторых конкретных условий реки Волга определены С.Л. Яцыно (1989).

Для построения аналитических моделей камер I типа возможно использовать следующее предложение С.Р. Гордеева и П.А. Михеева (1989).

Рассмотрим модель ската молоди рыб в самой простой речной системе, т.е. когда в русле нет притоков и рукавов. Разобьём русло на всей протяжённости точками 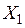, ,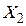…, 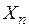на участки произвольной длины. Период времени, в течение которого происходит скат молоди, разобьём точками
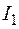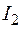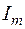, ,…, на интервалы .

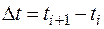Построение модели осуществляется для каждого вида рыб в отдельности с учётом стадий развития молоди: предличинка, личинка, ранняя молодь и т.д. Всю совокупность молоди данного вида разделим на группы следующим образом. Предположим, например, что личинка на начальной стадии имеет размер 6−7 мм и за время 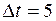сут. её размер увеличивается до
7−10 мм. За следующий промежуток 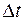она увеличивается до 13−15 мм, ещё за 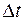− до 18−20 мм и т.д. Тогда к группе А¹ отнесём молодь размером от 5 до 10 мм, к группе А² − от 10 до 15 мм, к группе А³ − от 15 до 20 мм и т.д.

Распределение молоди по группам 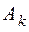, k = 1, 2, ….p обусловлено тем обстоятельством, что при переходе от группы к группе может значительно меняться как характер поведения особи, так и воздействия на неё различных внешних факторов.

Обозначим через 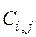концентрацию молоди в точке 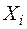в момент времени 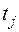и через 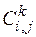− аналогичную концентрацию молоди k-ой возрастной группы.

Тогда .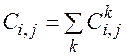

Предположим, что нам известны концентрации 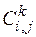для всех i и k в некоторый момент времени 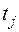. Проанализируем процессы, которые произойдут за время 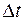и соответствующие изменения концентрации молоди. Во-первых, за это время представители группы 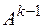перейдут в группу 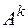за счёт своего развития во времени. Во-вторых, за счёт сноса молоди течением реки молодь из точки 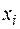переместится в какую-то другую точку русла, а её место займёт другая молодь. В-третьих, за счёт влияния неблагоприятных факторов произойдёт гибель её части, и, наконец, в-четвёртых, произойдёт очередной нерест, и появление новой группы молоди.

Будем считать, что концентрация от точки 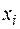до точки 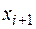меняется равномерно, кроме того, предполагается, что вся молодь из k-ой возрастной группы скатывается на участке 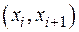в промежуток времени 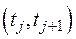с некоторой постоянной скоростью .

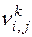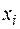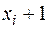Расстояние между точками и достаточно велико для того, чтобы особь могла преодолеть его за время 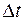. Поскольку все особи из группы 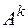на участке 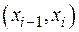скатываются во временном промежутке 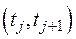со скоростью 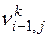, то за время 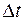они преодолевают расстояние 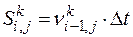. Поэтому, точки 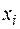в момент времени 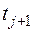достигнут те особи, которые в момент времени 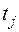находились на расстоянии 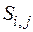вверх по течению. Обозначим эту точку через М (рисунок 3.5).

Рисунок 3.5 − Расчётная схема

Выясним, какая концентрация была в точке М в момент времени 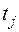. Так как в точке 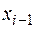концентрация была равна 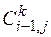, а в точке 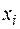− 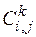, при этом, полагая, что между ними она менялась равномерно, то из простых математических соображений, концентрация в точке М равна

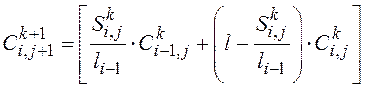. (3.3)

Если бы все особи выжили, то в момент времени 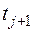концентрация в точке 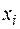представителей из группы 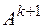совпадала бы с концентрацией в точке М, т.е. равнялась бы (3.3). Из-за воздействия различных факторов (хищники, болезни, техногенные воздействия и др.) происходит гибель части молоди. Поэтому

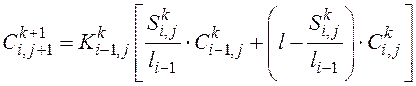, (3.4)

где 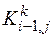− коэффициент выживаемости представителей k-ой группы на отрезке 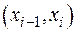в промежутке времени .

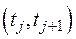Коэффициент выживаемости равен частному от деления количества выживших особей к исходному количеству особей. Поскольку неблагоприятное воздействие различных факторов может быть неоднородным в пространстве и во времени, то коэффициент выживаемости, вообще говоря, зависит и от пространственной переменной 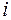и от временной .

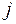Заметим, что поскольку в формулах (3.3) и (3.4) участвует выражение 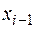, то они дают значение концентрации только в точках 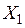, ,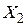…, 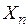. Для того чтобы прогнозировать концентрацию в точке 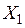, необходима информация о концентрации молоди выше точки 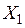по течению. Предположим, что такой информации мы не имеем. В таком случае, мы не можем прогнозировать концентрацию молоди в точке 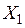в рамках данной модели без применения дополнительных соображений.

С учётом изложенного, получим зависимость для определения концентрации молоди 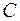в произвольной точке 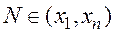в произвольный момент времени 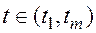в виде

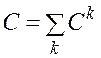, (3.5)

где 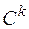− концентрация молоди k-ой группы в точке N.

Пусть точка N принадлежит отрезку 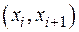, а 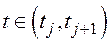. За время 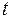- 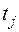особь на отрезке 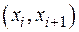скатилась на расстояние 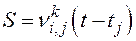. Поэтому в момент времени 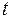в точку 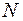попадают те особи, которые были в момент времени 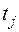выше по течению на расстоянии 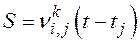, то есть в точке 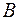(рисунок 3.6).

В этой точке в момент времени 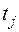концентрация равнялась, как это видно из рисунка 3.6, величине

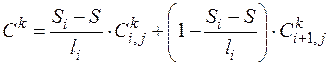. (3.6)

Рисунок 3.6 – Расчётная схема

Если бы все особи выживали, такая же концентрация была бы и в точке 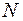в момент времени 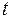. Однако не все особи выживают, поэтому необходимо внести поправочный коэффициент. Предположим, что процесс гибели носит равномерный характер. Тогда поправочный коэффициент 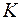связан с коэффициентом 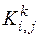из формулы (3.4) следующим соотношением

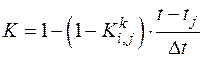. (3.7)

Окончательно формула (3.5) приобретёт вид

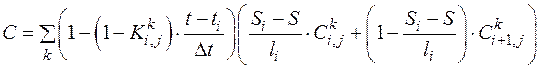. (3.8)

На основе зависимостей (3.4) и (3.8) полученных П.А. Михеевым и С.Р. Гордеевым для концентрации молоди можно записать подобные зависимости для интенсивностей ската молоди в камере 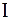типа 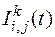при принятых нами обозначениях.

Для II типа камеры характерно значительное изменение интенсивности ската в выходном створе камеры по сравнению с входным створом за счёт впадения притока со скатывающейся молодью или выпуска молоди рыбоводным заводом. Створ на впадающем водотоке (обозначен ) располагается в непосредственной близости от принимающего потока (рисунок 3.7).

Протяжённость камеры по основному руслу невелика, поэтому переход молоди в следующую размерную группу в пределах камеры не происходит и, следовательно, уравнение связи для камеры II типа будет выглядеть следующим образом

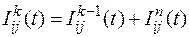, (3.9)

где 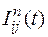− интенсивность ската молоди 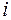-го вида 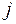-ой размерной группы через 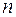-ый створ на притоке или на водовыпуске из рыбоводного завода.

а − схема 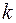-ой камеры; б − граф связи для 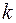-ой камеры

Рисунок 3.7 − Формализация камеры II типа

III тип камеры имеет место при делении русла реки на два рукава. При этом один из рукавов является основным, т.к. для него продолжается разбиение на камеры и разработка модели. В начале второго рукава, куда поступает доля расхода реки до деления равная 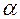, располагается створ 0. Предполагаем, что распределение молоди по рукавам пропорционально их расходам (рисунок 3.8).

а − схема 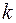-ой камеры; б − граф связи для 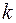-ой камеры

Рисунок 3.8 − Формализация камеры III типа

Протяжённость камеры по основному рукаву ограничена зоной деления потока и поэтому переход молоди в следующую размерную группу не происходит. Для камеры III типа можно записать

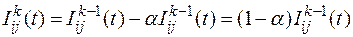, (3.10)

где 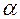− доля молоди (в относительных единицах), поступающая в не основной рукав.

Если где-то ниже по течению в пределах рассматриваемой ЛВХС РО происходит слияние не основного рукава с основным, то не основной рукав также разбивается на камеры и производится его моделирование до створа слияния. В узле слияния основного и не основного рукавов выделяется камера II типа и производится её моделирование в соответствии с зависимостью (3.9).

Камера IV типа предусматривает наличие водозабора, доля расхода которого от расхода реки равна (в относительных единицах) 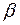(рисунок 3.9).

а − схема 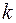-ой камеры; б − граф связи для 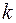-ой камеры

Рисунок 3.9 − Формализация камеры IV типа

Водозабор оборудован рыбозащитным устройством, рыбозащитная эффективность которого является известной. Конструкция РЗУ принципиального значения не имеет.

Математическая модель камеры IV типа имеет следующий вид

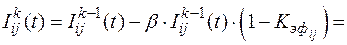
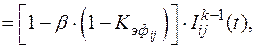(3.11)

где 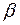− доля расхода водозабора:

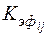− коэффициент эффективности РЗУ по 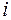-му виду и 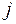-ой размерной группы.