Вопрос 1. Информационные основы технической диагностики

Получение информации об объекте – необходимое условие для постановки диагноза. В основе процесса получения и оценки информации лежит понятие «энтропия», изучаемое в термодинамике, также с ее помощью можно измерять информацию об объекте.

Вспомним основное правило: в самопроизвольных системах энтропия всегда возрастает, причем возрастание всегда сопровождается хаотическим разупорядочением. Книги и бумаги на столе обязательно приходят в беспорядок, если за ними не следить. Это результат случайной, а не организованной деятельности. Порядок создается искусственно и ему соответствует уменьшение энтропии. Неупорядоченное состояние всегда более вероятно, а вероятность количественно оценивается на основе накопленных статистических данных.

Зависимость энтропии от статистических характеристик впервые открыта Л.Больцманом в 1872 г. и имеет вид

,

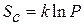где 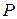– статистический вес системы;

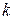– константа (постоянная Больцмана), Дж/К.

Физический смысл статистического веса 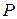заключается в числе способов существования системы или объекта при заданных условиях. Это целое положительное число.

Чем больше у системы возможностей отклонения от равновесного неупорядоченного состояния, тем интенсивнее возрастает статистическая энтропия, стремясь к максимальному значению (у системы из 4 элементов максимальный статистический вес 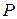равен 6, у системы из 6 элементов 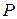уже будет равно 20, соответственно увеличится и ).

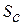Теперь коснемся связи между энтропией и информацией. С этой точки зрения энтропия есть мера нашего «незнания», мера недостатка информации о рассматриваемой системе. При подбрасывании монеты у нас могут произойти только два события – выпадение «орла» или выпадение «решки». Энтропия невелика, и информации дает одно из событий немного, так как вероятность появления события велика. При подбрасывании игральной кости энтропия растет, так как может произойти 6 событий, и каждое событие дает нам больше информации.

Реализация менее вероятного события дает больше информации. Этот постулат разработал американский инженер и математик К.Шеннон при разработке основ теории информации.

Очевидно, что при бросании двух игральных костей мы получаем вдвое больше информации. Таким образом, информация, получаемая в независимых сообщениях, суммируется, т.е.

,

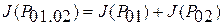где 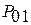, 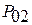– число равновероятных событий в первой и второй системах.

В то же время полное число равновероятных событий в двух независимых системах равно их произведению:

.

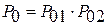Количество информации находится по формуле

.

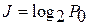Информация выражается в битах – двоичных единицах.

При длине алфавита 32 буквы: H = log₂ 32 = 5 бит (5 двоичных единиц).

Если перейти к состояниям технических объектов (систем), то очевидно, что появление неисправных состояний менее вероятно, чем исправных. Простой моделью такой системы может послужить та же игральная кость, у которой пять граней с цифрой 1 (исправное состояние), а одна – с цифрой 2 (неисправное состояние). Вероятность появления определенного состояния 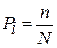, где 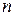, 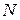– соответственно число реализованных и возможных событий в каждом из состояний 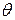. Если известно число возможных состояний системы 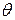, а также вероятность их появления, то можно оценить максимальную неопределенность системы или степень ее возможной изменчивости

.

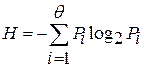Эта зависимость называется информационной энтропией.