Уравнение плоской волны, движущейся в произвольном направлении. Фазовая скорость и скорость распространения энергии
Пусть плоская волна движется в направлении орта 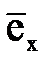 . В начале координат напряженность электрического поля
. В начале координат напряженность электрического поля 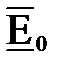 , а напряженность магнитного поля
, а напряженность магнитного поля 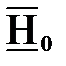 . Найдем значения векторов поля в точке А, положение которой задано вектором
. Найдем значения векторов поля в точке А, положение которой задано вектором 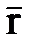 (рис. 7.4). Предположим, что среда не имеет потерь (
(рис. 7.4). Предположим, что среда не имеет потерь ( 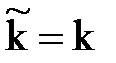 ).
).

Рис. 7.4. Распространение плоской волны в направлении s
Если через точку A провести плоскость, нормальную к направлению распространения волны, то на всей этой плоскости векторы поля в любой произвольный момент времени будут иметь одно и то же значение, так как волна плоская. От начала координат до указанной плоскости волна прошла путь 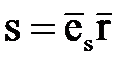 , следовательно, в точке
, следовательно, в точке 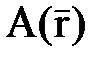 фаза изменилась на
фаза изменилась на 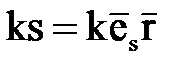 . Таким образом,
. Таким образом, 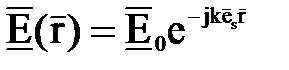 и
и 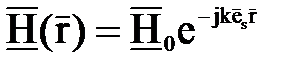 Эти выражения можно записать более компактно, если воспользоваться понятием волнового вектора
Эти выражения можно записать более компактно, если воспользоваться понятием волнового вектора
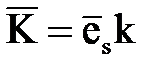 , (7.20)
, (7.20)
модуль которого равен волновому числу, а направление совпадает с направлением распространения волны. Подставив (7.20) в предыдущее выражение, получим уравнения движения плоской волны в произвольном направлении
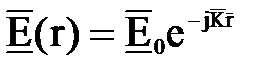 и
и 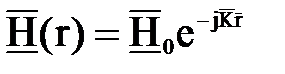 . (7.21)
. (7.21)
Запишем уравнения распространения волны в декартовой системе координат. Для этого скалярное произведение векторов 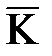 и
и 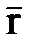 необходимо представить в декартовой системе.
необходимо представить в декартовой системе.
Радиус-вектор точки наблюдения 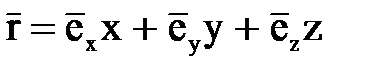 . Волновой вектор также можно представить в виде суммы трех составляющих:
. Волновой вектор также можно представить в виде суммы трех составляющих: 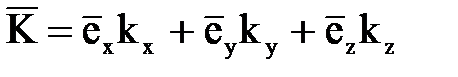 .
.
Перемножим скалярно 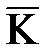 и
и  :
: 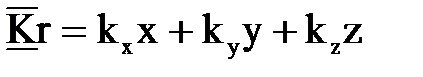 . Подставив это выражение в (7.21), получим
. Подставив это выражение в (7.21), получим
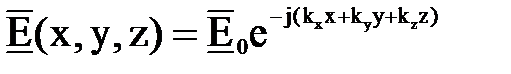 ,
,
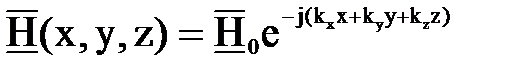 .
.
Теперь можно записать мгновенное значение любой из составляющих векторов поля 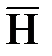 и
и 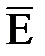 . Например, если в начале координат
. Например, если в начале координат 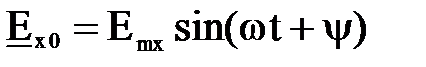 , то в точке с координатами х, у, z в момент времени t
, то в точке с координатами х, у, z в момент времени t
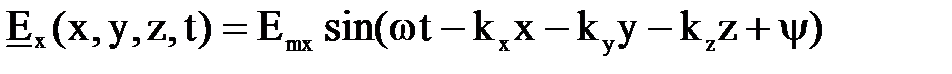 . (7.22)
. (7.22)
Совершенно аналогичные выражения можно записать для двух других составляющих вектора 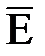 , а также для всех трех составляющих вектора
, а также для всех трех составляющих вектора 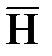 .
.
При изучении теории длинных линий в режиме установившихся синусоидальных колебаний фазовая скорость была определена как скорость перемещения вдоль линии передачи, например кабеля связи, точки, в которой фаза колебаний одинакова. Совершенно аналогичное определение можно дать, рассматривая распространение в пространстве плоской моногармонической электромагнитной волны. Однако в этом случае слово «линия» следует понимать в геометрическом смысле как некоторую прямую, не обязательно совпадающую с направлением распространения волны.
Предположим, что волна распространяется в направлении, определяемом ортом 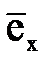 , которое образует угол a с направлением оси х (рис. 7.5). Уравнение движения волны для одной из составляющих векторов поля в соответствии с (7.22) можно записать так:
, которое образует угол a с направлением оси х (рис. 7.5). Уравнение движения волны для одной из составляющих векторов поля в соответствии с (7.22) можно записать так:
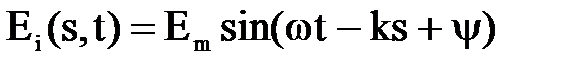 .
.

Рис. 7.5. Длина волны в произвольном направлении х
Зафиксируем некоторое значение фазы 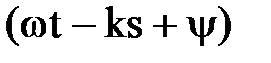 =const. Расстояние от начала координат до точки, в которой колебания находятся в данной фазе, изменяется со временем равно
=const. Расстояние от начала координат до точки, в которой колебания находятся в данной фазе, изменяется со временем равно 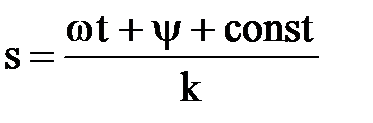 . Следовательно, фазовая скорость в направлении s будет равна
. Следовательно, фазовая скорость в направлении s будет равна
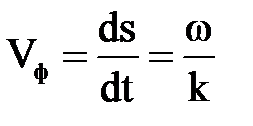 (7.23)
(7.23)
Из (7.19) следует, что скорость распространения электромагнитной волны также равна 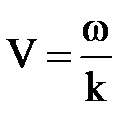 . Таким образом, в направлении распространения фазовая скорость совпадает со скоростью движения волны, а следовательно, и со скоростью распространения энергии.
. Таким образом, в направлении распространения фазовая скорость совпадает со скоростью движения волны, а следовательно, и со скоростью распространения энергии.
Уравнение движения волны можно записать и в форме (7.22). Из этого выражения следует, что фазовая скорость в направлении х, т. е. скорость движения точки, в которой фаза колебаний ( 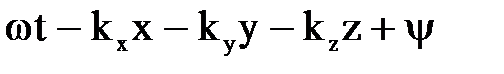 ) остается постоянной, равна
) остается постоянной, равна
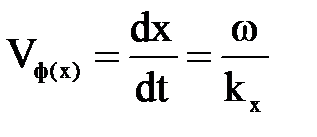 . (7.24)
. (7.24)
Так как 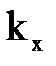 - проекция на направление оси х волнового вектора
- проекция на направление оси х волнового вектора 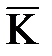 , то
, то 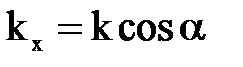 , следовательно,
, следовательно,
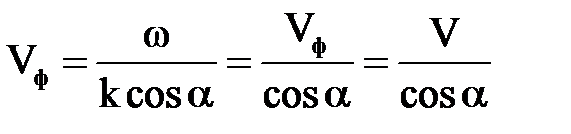 . (7.25)
. (7.25)
Таким образам, фазовая скорость в направлении, не совпадающим с направлением распространения волны, всегда больше волновой скорости. Если волна распространяется в пустом пространстве (волновая скорость равна скорости света с), фазовая скорость в произвольном направлении будет больше скорости света.
Это положение можно проиллюстрировать с помощью следующих наглядных представлений. На рис. 7.5 штриховыми линиями показаны «гребни волны», распространяющейся в направлении 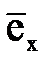 . («Гребнем волны» можно считать геометрическое место точек, в которых вектор поля имеет одинаковое значение.) Расстояние между гребнями равны длине волны в направлении движения, т. е. тому пути, который волна проходит за период
. («Гребнем волны» можно считать геометрическое место точек, в которых вектор поля имеет одинаковое значение.) Расстояние между гребнями равны длине волны в направлении движения, т. е. тому пути, который волна проходит за период
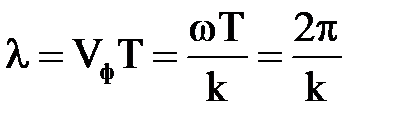 . (7.26)
. (7.26)
Расстояния между гребнями в направлении х, т. е. длина волны в направлении х, больше, чем в направлении 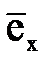 :
:
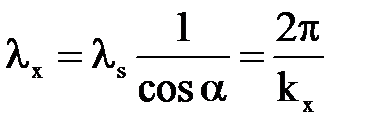 .
.
Следовательно, за то же время Т «гребень волны» проходит в направлении х больший путь, т. е. фазовая скорость в направлении х больше, чем фазовая скорость в направлении движения волны.
Это утверждение не противоречит одному из основных положений физики о том, что скорость распространения энергии не может быть больше скорости света. Фазовую скорость нельзя отождествлять со скоростью распространения энергии. Энергия распространяется в направлении движения волны. Скорость распространения энергии в направлении оси х надо рассматривать как проекцию скорости  на
на 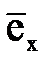 , т. е.
, т. е. 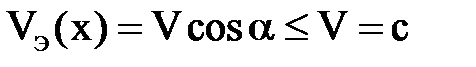 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| Для спрощення розрахунків визначаємо Рб , Рп , Рс , вважаючи, що бандажі й | | | Неравновесные электрохимические процессы. Электролиз |
Дата добавления: 2015-12-16; просмотров: 1560;
