Теорема Умова - Пойнтинга

Анализируя систему уравнений Максвелла, можно сделать выводы о распределении и распространении энергии электромагнитного поля в пространстве, а также об энергетических преобразованиях в электромагнитном поле. Этот анализ основывается на теореме Умова - Пойнтинга, соответствующей закону сохранения энергии.

Введем новый вектор, равный

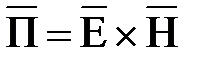(2.4)

Этот вектор называется вектором Пойнтинга и имеет размерность Вт/м².

Для этого вектора справедлива следующая теорема (теорема Умова - Пойнтинга):

поток вектора Пойнтинга, входящий внутрь замкнутой поверхности, равен сумме мощности тепловых потерь и скорости изменения энергии электромагнитного поля внутри объема, ограниченного этой поверхностью.

Математическая формулировка теоремы запишется так

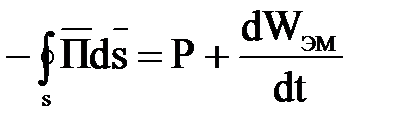, (2.5)

причем W_эм=W_э+W_м.

Доказательство теоремы основывается на уравнениях Максвелла. Запишем для произвольной точки, находящейся внутри объема

.

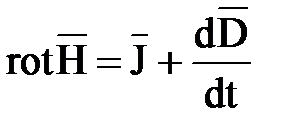Видно, что если это уравнение умножим скалярно на 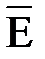, то в правой части получим плотность мощности тепловых потерь и мощности электрического поля

.

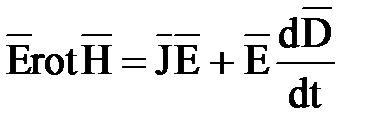Аналогично, умножив второе уравнение Максвелла на 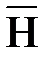, в правой части получим плотность мощности магнитного поля

.

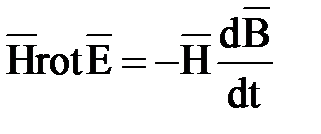Образовав разность, получим полную мощность электромагнитного поля

.

Применяя правило векторного анализа к левой части полученного выражения, преобразуем разность к виду

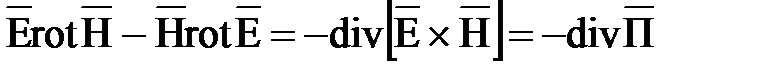
и получим дифференциальную форму записи теоремы Умова - Пойнтинга

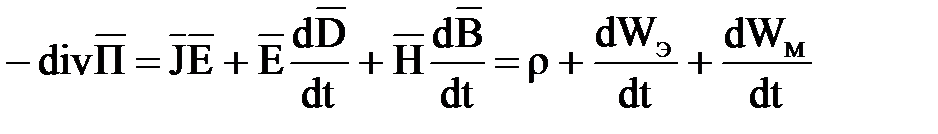. (2.6)

Для записи теоремы в интегральной форме проинтегрируем левую и правую части выражения (2.6) по всему объему

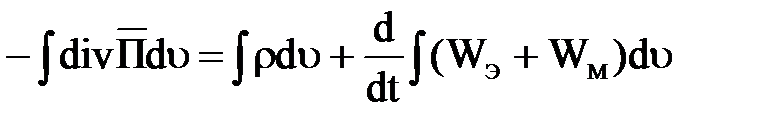
или, с учетом теоремы Остроградского - Гаусса, получим

.

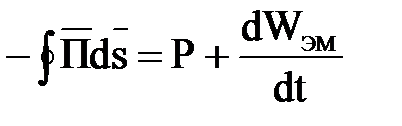Зная распределение вектора 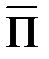в пространстве, можно судить о том, как распространяется электромагнитная энергия.