Потенциалы электромагнитного поля.
Энергетические соотношения электродинамики.
Предположим, что в некотором V действуют источники электромагнитного поля. на вопрос как складывается баланс энергии (мощности) поля для этого объема ? Можно закон сохранения энергии электромагнитного поля.
div 
= - 
,
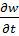где w объемная энергии поля (аналог g - объемной плотности зарядов).
П(ВТ/м2) - плотность потока мощности поля.
Энергия электромагнитного поля в единице объема
Следовательно поток вектора Пойтинга сквозь замкнутую поверхность, ограничивающую объем V равен мощности, в объеме V в виде теплоты и мощности, идущей на ЭН энергии.
Потенциалы электромагнитного поля.
Кроме величины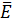 
и 
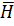характеризующих электромагнитное поле существует 
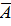- векторный потенциал и φск - скалярный потенциал электромагнитного поля. Целый ряд задач теории электромагнитного поля при использовании 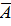и φск решается легче, чем основываясь на использовании векторов E и H. Установим связь между 
, 
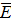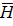и 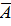, φск . По определению 
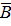=rot 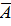. Действительно, из уравнения Максвелла divB= 0 (тождественно) отсюда В=rot 
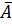, что и требовалось доказать.
Если B=μa*H то H=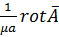 
(9)
A - векторный электродинамический потенциал поля.
Исходя из уравнения Максвелла
rot = -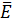 
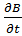
rot = -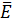 
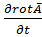или
= 
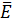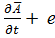
В электростатике имеет соотношение
= 
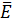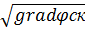(11)
Выбираем в качестве константы С 
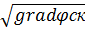= и тогда в переменном поле
= - 
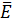(12)
Соотношения (9) и (12) определяют правила вычисления напряженности поля при известных потенциалах 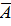и φск
Дата добавления: 2015-12-16; просмотров: 760;