Волновые уравнения и электродинамические потенциалы
Для решений уравнений электромагнитного поля их обычно приводят к волновым уравнениям. То есть уравнения Максвелла преобразуют волновые уравнения. Волновыми называются такие дифференциальные уравнения второго порядка в частных производных, которые описывают распространение колебаний в среде. Они содержат наряду с пространственными производными второго порядка также вторые производные по времени. От уравнений Максвелла можно перейти к волновым уравнениям для:
- векторов электромагнитного поля;
- электродинамических потенциалов;
- волновым уравнениям для вектора Герца.
Для получения волнового уравнения, для 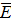 исключим из уравнений Максвелла вектор
исключим из уравнений Максвелла вектор 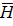 . Для этого продифференцируем по времени первое уравнение Максвелла rotH=gпр +gсн-gэст= gэст +
. Для этого продифференцируем по времени первое уравнение Максвелла rotH=gпр +gсн-gэст= gэст + 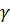 э
э 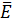 +𝜀a
+𝜀a 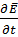 =gп
=gп
где gэст - плотности стороннего электрического тока
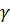 э проводимость среды
э проводимость среды
И умножим на
μa
μa 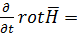 μa
μa  (
( 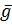 эст+
эст+ 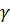 э
э 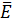 +𝜀a
+𝜀a 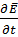 ) (1).
) (1).
Затем из второго уравнения Максвелла найдем rot*rot+ 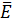
-μа 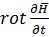 = rot*rot
= rot*rot 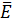 rotE=-
rotE=- 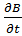 (2).
(2).
Изменим порядок дифференцирования в (1) и сложим уравнений (1) и (2).
Используй известное соотношение rot*rotE=grad*dive-Δ2E и учитывая третье уравнение Максвелла div 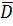 =ρ будем окончательно иметь
=ρ будем окончательно иметь
˅2E-μa𝜀a 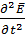 -μa
-μa 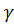 э
э 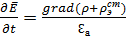 + μa
+ μa 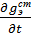 (1)
(1)
Уравнение (1) называется обобщенным неоднородным векторным волновым уравнением в случае диэлектрика 𝛾э=0 слагаемое уравнение μaγэ 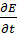 и (1) переходит в неоднородное векторное волновое уравнение или векторное уравнение Даламбера. Если в области, в которой рассматривается электромагнитное поле γэ=0 и отсутствуют накопленное ρ=0 и сторонние электрические заряды
и (1) переходит в неоднородное векторное волновое уравнение или векторное уравнение Даламбера. Если в области, в которой рассматривается электромагнитное поле γэ=0 и отсутствуют накопленное ρ=0 и сторонние электрические заряды 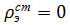 и токи
и токи 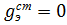 то правая часть уравнения (1) равна нулю и оно приобретает вид однородного векторного волнового уравнения Δ 2
то правая часть уравнения (1) равна нулю и оно приобретает вид однородного векторного волнового уравнения Δ 2 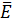 - μa𝜀a
- μa𝜀a 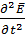 =0 (2)
=0 (2)
Аналогично находят уравнения для вектора 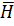 для этого необходим взять от обеих частей первого уравнения Максвелла взять rot , а второе уравнение продифференцировать во времени и полученный результат умножить на 𝜀a .
для этого необходим взять от обеих частей первого уравнения Максвелла взять rot , а второе уравнение продифференцировать во времени и полученный результат умножить на 𝜀a .
После таких преобразований и сложений с учетом уравнения Максвелла будем иметь Δ 2 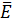 - μa𝜀a
- μa𝜀a 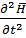 - μa
- μa 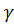 э
э 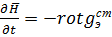 (3)
(3)
из уравнений (1) и (3) следует что они имеют один и тот же вид и отличаются только правой (известной) части.
При гармонических (монохроматических) источниках введения комплексных амплитуд позволяют упростить волновые уравнения поля. Так, например, после подстановки в место 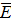 вводится комплексное значение
вводится комплексное значение 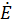 m*ejwt после подстановки комплексных векторов в рассмотренные волновые уравнения и последующего деления обеих частей этого уравнения на временной множитель ejwt получают следующие неоднородные дифференциальные уравнения
m*ejwt после подстановки комплексных векторов в рассмотренные волновые уравнения и последующего деления обеих частей этого уравнения на временной множитель ejwt получают следующие неоднородные дифференциальные уравнения
Δ 2 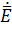 + r2
+ r2 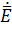 =
= 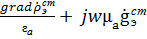
Δ 2 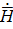 + r2
+ r2 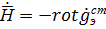
где r2 = w2μa𝜀a – комплексное волновое число
Дата добавления: 2015-12-16; просмотров: 2153;
