Вектор Умова–Пойтинга
Напомним, что если в электромагнитной волне вектор 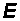 имеет единственное направление (а, следовательно, единственное направление имеет и вектор
имеет единственное направление (а, следовательно, единственное направление имеет и вектор 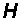 ), то волна называется линейно-поляризованной. Ниже будут приведены доказательства того, что свет представляет собой электромагнитные волны, частоты которых лежат в определенном интервале. Если в световой волне вектор
), то волна называется линейно-поляризованной. Ниже будут приведены доказательства того, что свет представляет собой электромагнитные волны, частоты которых лежат в определенном интервале. Если в световой волне вектор 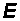 (и
(и 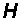 ) имеет всевозможные направления, то такой свет принято называть естественным. Следовательно, свет как плоская электромагнитная волна может быть в однородной среде как естественным, так и линейно-поляризованным.
) имеет всевозможные направления, то такой свет принято называть естественным. Следовательно, свет как плоская электромагнитная волна может быть в однородной среде как естественным, так и линейно-поляризованным.
Электромагнитная волна может переносить электромагнитную энергию (поток энергии). Вычислим поток электромагнитной энергии в вакууме, исходя из уравнений Максвелла. Для этого умножим обе стороны уравнения (12.1) скалярно на 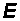 , а обе стороны уравнения (12.2) – на
, а обе стороны уравнения (12.2) – на 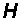 :
:
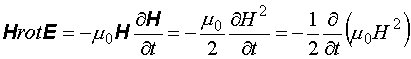 , (12.18)
, (12.18)
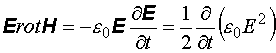 . (12.19)
. (12.19)
Используем формулу векторного анализа
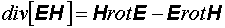
и, соответственно, вычтем из уравнения (12.18) выражение (12.19):
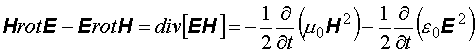 . (12.20)
. (12.20)
Выражение (12.20) представляет собой запись закона сохранения энергии электромагнитного поля в дифференциальной форме. Рассмотрим физический смысл отдельных величин, входящих в уравнение (12.20). Частная производная 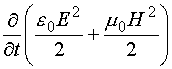 представляет собой приращение электромагнитной энергии единицы объема за единицу времени, a
представляет собой приращение электромагнитной энергии единицы объема за единицу времени, a 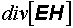 – поток энергии, вытекающей из единицы объема за единицу времени. Вектор
– поток энергии, вытекающей из единицы объема за единицу времени. Вектор  представляет собой поток энергии через единичную площадку, расположенную перпендикулярно потоку. При
представляет собой поток энергии через единичную площадку, расположенную перпендикулярно потоку. При 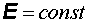 и
и 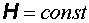 поток постоянен и вектор
поток постоянен и вектор  выражает поток энергии за единицу времени, при переменных
выражает поток энергии за единицу времени, при переменных 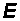 и
и 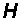 он выражает мгновенное значение потока.
он выражает мгновенное значение потока.
Введем обозначение:
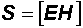 , (12.21)
, (12.21)
где 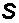 называют вектором Умова–Пойнтинга. Этот вектор определяет направление распространения энергии волны.
называют вектором Умова–Пойнтинга. Этот вектор определяет направление распространения энергии волны.
Вычислим вектор Умова–Пойнтинга плоской электромагнитной волны:
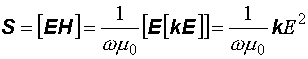 . (12.22)
. (12.22)
Согласно выражению (12.22), векторы S и k коллинеарны. Это справедливо только для вакуума и изотропных сред. В анизотропных средах, в которых физические свойства различны для разных направлений, это условие в общем случае не выполняется. Используем ранее введенный единичный вектор m, направленный вдоль распространения волны 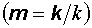 .
.
 Поскольку для вакуума
Поскольку для вакуума 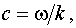 то
то
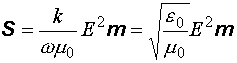 . (12.23)
. (12.23)
Найдем соотношение между абсолютными значениями векторов 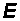 и
и 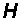 в плоской волне. Из уравнений (12.15) и (12.16) имеем:
в плоской волне. Из уравнений (12.15) и (12.16) имеем:
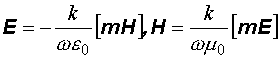 . (12.24)
. (12.24)
Имея в виду, что 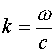 , получим:
, получим:
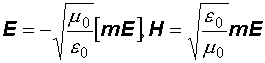 . (12.25)
. (12.25)
Учитывая, что векторы 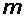 ,
, 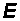 ,
, 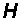 взаимно перпендикулярны, находим соотношение между абсолютными значениями векторов
взаимно перпендикулярны, находим соотношение между абсолютными значениями векторов 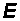 и
и 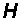 :
:
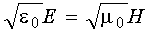 . (12.26)
. (12.26)
Из общего определения плотности электромагнитной энергии в вакууме


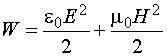 . (12.27)
. (12.27)
С учетом уравнения (12.11) для плоской волны получим
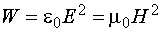 . (12.28)
. (12.28)
Запишем теперь окончательное выражение для вектора Умова–Пойнтинга в плоской волне:
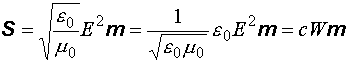 . (12.29)
. (12.29)
Полученное равенство имеет простой смысл. Через единичную площадку, поставленную перпендикулярно распространению волны, в единицу времени проходит энергия, заключенная в цилиндре с площадью основания, равной единице, и высотой 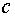 .
.
Дата добавления: 2016-01-29; просмотров: 1431;
