Электромагнитные волны. Из уравнений Максвелла следует важный вывод о существовании принципиально нового физического явления: электромагнитное поле способно существовать

Из уравнений Максвелла следует важный вывод о существовании принципиально нового физического явления: электромагнитное поле способно существовать самостоятельно - без электрических зарядов и токов. При этом изменение его состояние обязательно имеет волновой характер. Поля такого рода называют электромагнитными волнами. В вакуум они всегда распространяются со скоростью света с.Присутствие тока смещения 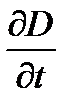наряду с величиной 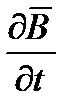обусловливает возможность появления электромагнитных волн.

Всякое изменение во времени магнитного поля возбуждает поле электрическое, изменение же поля электрического в свою очередь возбуждает магнитное поле. За счет непрерывного взаимопревращения или взаимодействия они должны сохраняться и электромагнитное возмущение будет распространяться в пространстве.

Основные свойства электромагнитных волн.

1). Скорость распространения в непроводящей нейтральной неферромагнитной среде

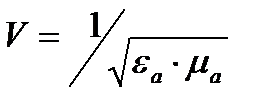где

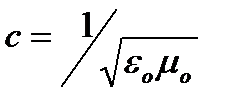
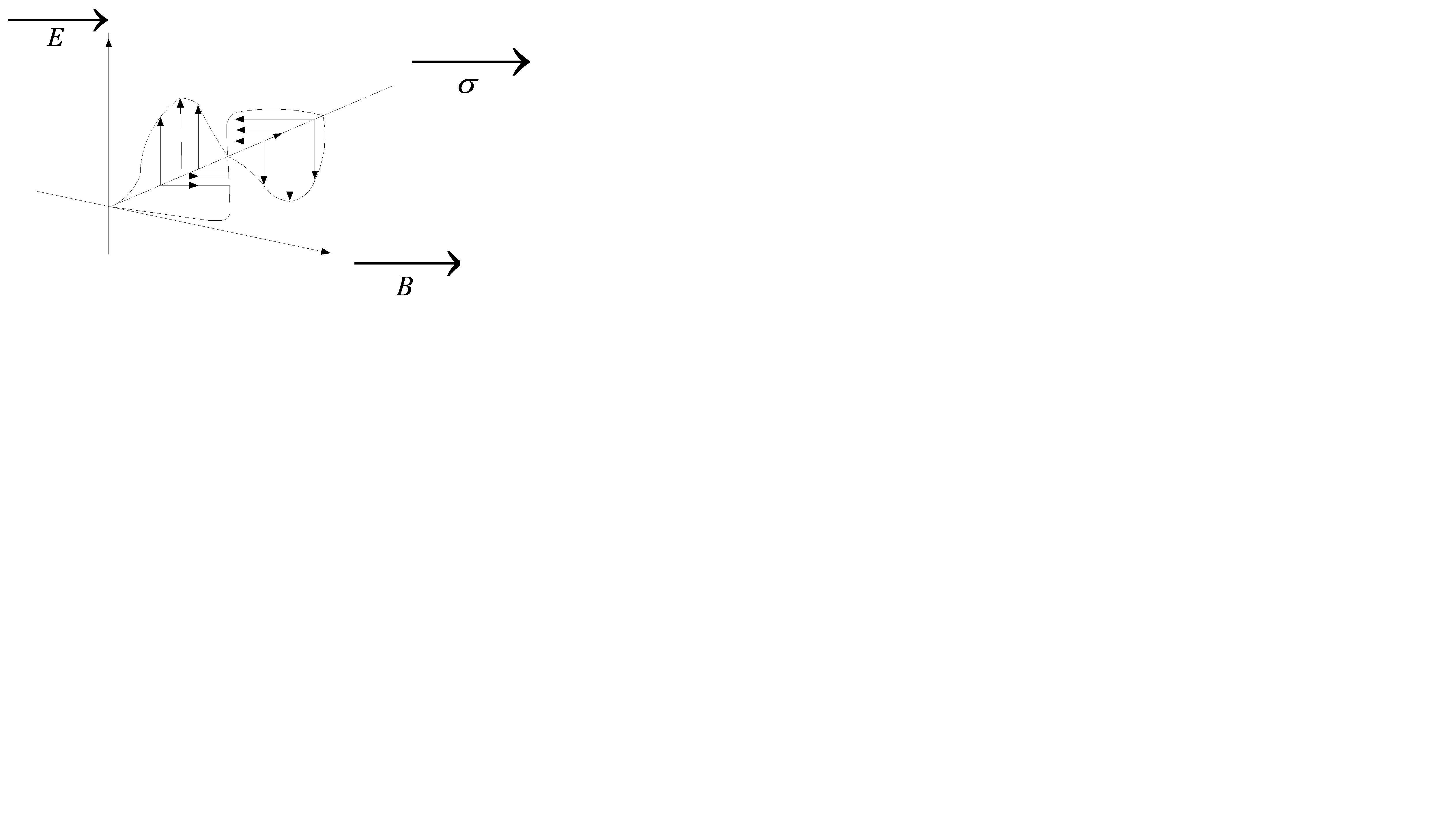
2). Вектор 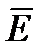, 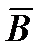и 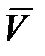(скорость волны) взаимно перпендикулярны и образуют правую систему.

3). В электромагнитной волне векторы 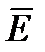, 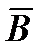всегда колеблются в одинаковых фазах, при чем между мгновенными значениям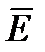и и 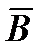в любой точке существует определенная связь, а именно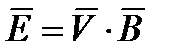

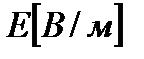
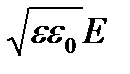
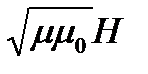
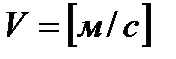
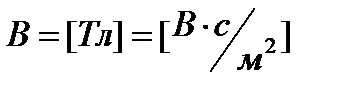
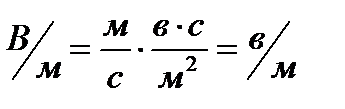
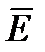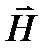Это значит, что и (или 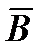) одновременно достигают максимума, одновременно обращаются в нуль.

6. Уравнения Максвелла в комплексной форме записи. Уравнения 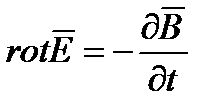и 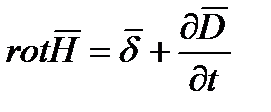записаны для мгновенных значений. Есл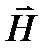и и 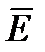изменяются во времени синусоидально, то можно воспользоваться символическим методом и записать уравнения в иной форме. Пусть **** (измен. синусоидально)

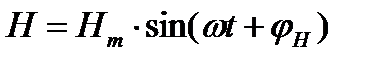
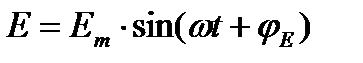
Окончательно первое уравнение Максвелла в комплексной форме записи в дифференциальной форме запишется как

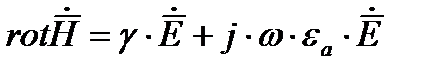
j - означает мнимую***

Знак ( ) означает, что проекция вектора на любую из координатных осей во времени изменяются синусоидально.

Второе уравнение Максвелла в комплексной форме записи в дифференциальной форме запишется как

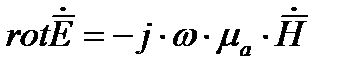
7. Теорема Умова – Пойнтинта для мгновенных значений.

Кроме уравнений Максвелла, большое значение в теории электромагнитного поля имеет теорема Умова-Пойнтинта, которая описывает энергетическое соотношение в поле.

Энергия электрического поля в единице объема равна .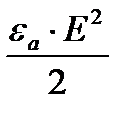

Энергия магнитного поля в единице объема равна ,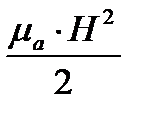

Энергия в объеме dV равна (в единицу времени)

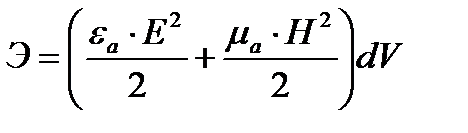
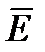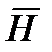Обозначим векторное произведение на через 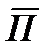, то есть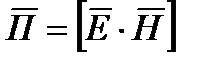

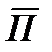- это вектор называемый вектором Пойнтинта.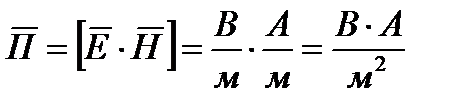

Размерность вектора Пойнтинта имеет размерность мощности, или энергии в единицу времени отнесенной к единице поверхности и направления его совпадает с направлением движения правого винта, если головку которого вращать по кротчайшему пути от 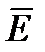к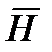

Теорема Умова-Пойнтинта для мгновенных значений записывается следующим образом:

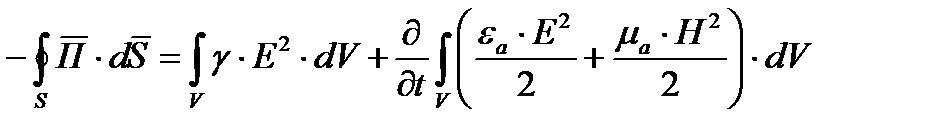(1)

Левая часть уравнения представляет собой поток вектора Пойнтинта (направленные внутрь объема) сквозь любую замкнутую поверхность S, ограничивающую некоторый объем V.

Знак (-) в левой части формулы объясняется следующим образом. Элемент поверхности 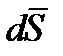в любой ее точке направлен в сторону внешней, по отношению к рассматриваемому объему нормали. Вектор Пойнтинта направлен внутрь этого объема. Поскольку угол между 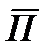и 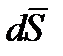>90, то скалярное произведение 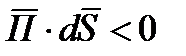, а 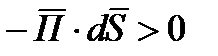. Таким образом за счет знака (-) левая часть формулы (1) положительна.

В соответствии с уравнением Джоуля – Ленца в дифференциальной форме 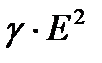- энергия, выделяемая в виде теплоты в единице объема в единицу времени. Поэтому 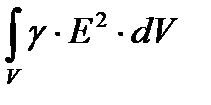есть энергия, выделяемая в виде теплоты в единицу времени в объеме V.

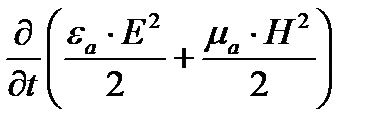есть скорость изменения запаса энергии в единице объема. Но скорость изменения электромагнитной энергии есть мощность. Следовательно, поток вектора Пойнтинта сквозь любую замкнутую поверхность, ограничивающую объем ____, равен мощности, выделяющейся в объеме____ в виде теплоты и мощности, идущей на приращение энергии электромагнитного поля.

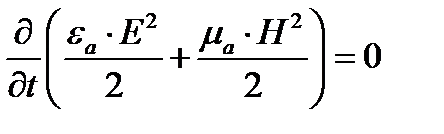Теорему Умова-Пойнтинта следует трактовать как уравнение энергетического баланса. Левая часть есть мощность или энергия в единицу времени, доставляемая в виде потока вектора Пойнтинта внутрь некоторого объема, правая часть есть энергия, расходуемая в единицу времени внутри объема. Соотношение (1) было получено в предположении, что среда внутри объема V однородна и изотропна, а так же в предположении, что отсутствует отраженная волна и внутри объема нет источников электродвижущей силы. Если поле не изменяется во времени, то

Обратим внимание на то, что выражение (1) учитывает возможность прохождения потока вектора Пойнтинта 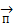транзитом через объемV. Электромагнитная энергия от места ее генерирования передается к месту потребления по диэлектрику. Проводники же в линиях передачи выполняют двоякую роль. Они являются каналами, по которым проходит ток, и организаторами структуры поля в диэлектрике.

Пусть энергия постоянного тока передается по коаксиальному кабелю.

Радиус жилы 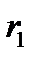, внутренней оболочки 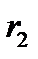. Примем проводимость материала жилы и оболочки настолько большой 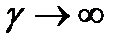, что напряженность поля 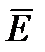в жиле

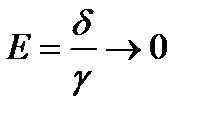
Пространство между жилой и оболочкой заполнено диэлектриком. Докажем, что энергия, передаваемая приемнику в единицу времени, равна 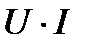, действительна канализируется по диэлектрику. С этой целью подсчитаем поток вектора Пойнтинта через поперечное кольцо с внутренним радиусом 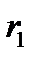и наружным 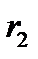. Напряженность магнитного поля в диэлектрике по закону полного тока 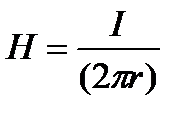. (1)

Напряженность электрического поля в диэлектрике при постоянном токе определяется так же, как и в условиях электростатики.

(2)

Где Q - полный заряд жилы на длине l;

U - напряжение между жилой и оболочкой.

Следовательно, в некоторой точке диэлектрика, расположенной на расстоянии *** от оси ( )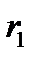

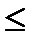
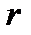
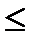
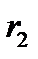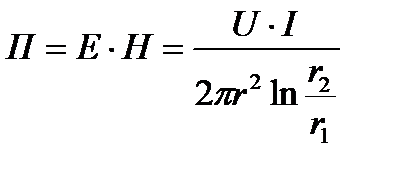из (1) и (2)

Отсюда поток вектора Пойнтинта через кольцо радиусам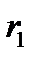и и 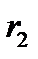будет определяться как

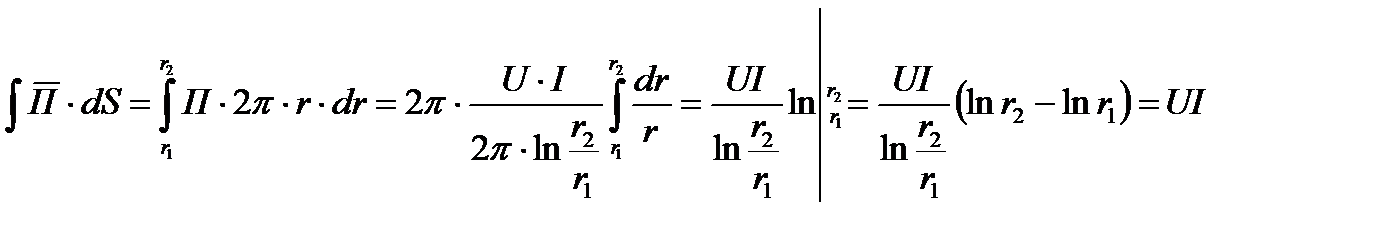
Таким образом, вся поступающая к приемнику энергия передается по диэлектрику. По жиле и оболочке энергия к приемнику не передается. Более того, если учесть, что 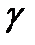конечна и напряженность электрического поля в жиле и оболочке направлена по току и не равна нулю, то существует не равный нулю вектор Пойнтинта, направленный через боковую поверхность провода внутрь провода. То есть провода сами потребляют из диэлектрика энергию на покрытие тепловых потерь.

Пример.

Определить тангенс угла 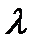, составляемого напряженностью электрического поля с нормалью к поверхности жилы в точке, принадлежащей поверхности жилы коаксиального кабеля, а так же подсчитать величину потока вектора Пойнтинта через боковую поверхность жилы на длине в 1м и сопоставить величину потока вектора Пойнтинта с потерями энергии в жиле на длине в 1м. Радиус медной жилы 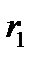=0,3cм. Внутренний радиус оболочки 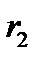=1cм. Протекающий по кабелю постоянный ток I=50A. Напряжение между жилой и оболочкой U= .

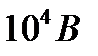Нормальная составляющая напряженности электрического поля на поверхности жилы будет

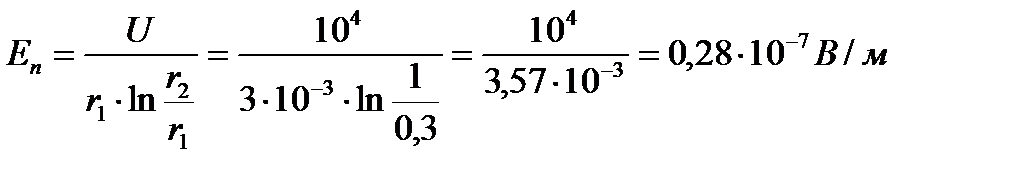
Тангенциальная составляющая напряженности электрического поля на поверхности жилы по закону Ома будет

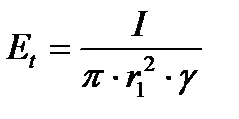
Поясним вывод этой формулы:

Закон Ома в дифференциальной форме

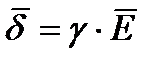; отсюда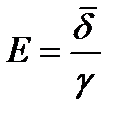

С другой стороны 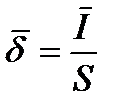, отсюда 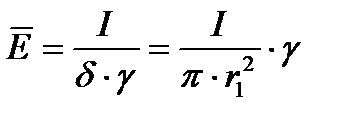что и требовалось доказать.

Отсюда из найденных 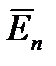и 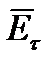вектор напряженности электрического поля составляет с нормалью к поверхности жилы угол 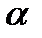, тангенс которого равен

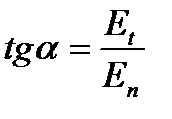
Циркуляция напряженности магнитного поля на поверхности жилы по закону полного тока составит:

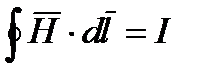, отсюда контур интегрирования будет 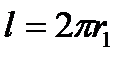, и

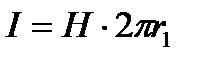, отсюда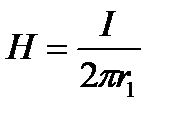

Для определения величины потока вектора Пойнтинта внутри жилы на длине в 1м следует умножить составляющую вектора Пойнтинта 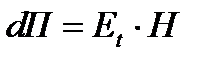, проникающую внутрь жилы на величину боковой поверхности жилы на длине в 1м.

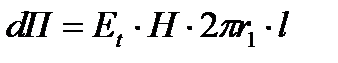
Вычислим значение этой составляющей вектора Пойнтинта для медной жилы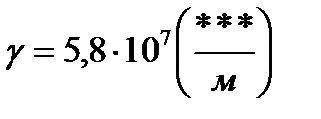

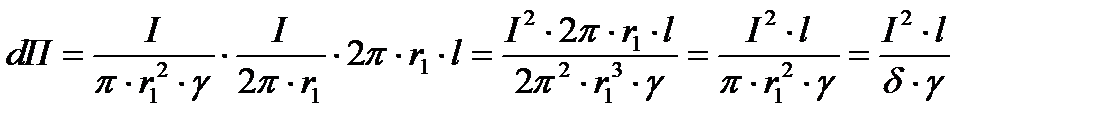
Определим величину потерь энергии в единицу времени в центральной жиле кабеля на длине 1м.

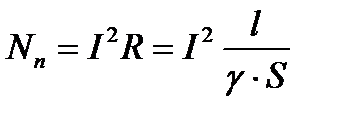
Отсюда делаем вывод, что 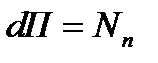или величина потока вектора Пойнтинта внутри жилы на длине в 1м равна мощности, теряемой электрическим током в центральной жиле на длине в 1м.

Этим самым подтверждается утверждение о том, что при конечном 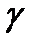, , 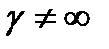существует составляющаяся напряженности электрического поля в жиле и оболочке и направлена по току и не равна нулю. Таким образом, существует поток вектора Пойнтинта через боковую поверхность внутрь провода, то есть провода сами потребляют из диэлектрика энергию на покрытие тепловых потерь. Если эти потери будут очень большими то провода могут расплавиться.