Плоские электромагнитные волны

Особенности электромагнитных волн, способы их возбуждения и законы распространения описываются уравнениями Максвелла.

В реальных средах электромагнитные волны, как и волны любой природы, испытывают отражение и преломление, интерференцию, дифракцию, поляризацию.

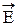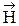Вид поляризации и ряд других особенностей электромагнитных волн задаются, или природой источника излучения, или свойствами среды.Пространственное распределение электромагнитных полей, временные зависимости (t) и (t), определяют тип волн (плоские, сферические и др.).

Теория электродинамики Максвелла позволила установить, что радиоволны, видимый свет, рентгеновское, инфракрасное, ультрафиолетовое и гамма-излучения представляют собой электромагнитные волны с различной длиной волны (табл. 6.1).

Существование электромагнитных волн было предсказано Фарадеем, а затем Максвелл обосновал их существование. Герц экспериментально подтвердил справедливость теории Максвелла.

Если возбудить с помощью колеблющейся системы (вибратора Герца, электрического диполя и др.) переменное электромагнитное поле, то в окружающем пространстве возникнет последовательность взаимно превращающихся друг в друга переменных электрических и магнитных полей, распространяющихся от точки к точке в виде электромагнитных волн (рис.6.7). Этот процесс является периодическим во времени и в пространстве.

Таблица 1

n, Гц	l, м	Диапазон	Источники возбуждения
10³ 10¹² 3,7×10¹⁴ 7,5×10¹⁴ 3×10¹⁷ 3×10²⁰ 10²³	3×10⁵ 30×10^-⁴ 8×10^-⁷ 4×10^-⁷ 10^-⁹ 10^-¹² 3×10^-¹⁵	Радиоволны К-излучение Видимый свет УФ-излу- чение Рентген g - излучение	Переменные токи в проводниках и П пучках электронов: генераторы СВЧ и радиочастот Излучение атомов (молекул) при их нагревании или электрическом воздействии Излучение атомов под действием ускоренных электронов Атомные процессы при воздействии ускоренных заряженных частиц Ядерные процессы, радиоактивные распады, космические процессы

Существование электромагнитных волн вытекает из уравнений Максвелла, которые описываются волновыми уравнениями для векторов 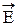и 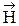соответственно:

Рис. 7

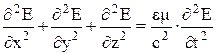, (17)

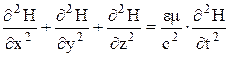, (18)

где

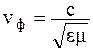. (19)

Уравнения (17) и (18) неразрывно связаны друг с другом, так как они получены из уравнений Максвелла. В дальнейшем будем рассматривать плоскую электромагнитную волну, распространяющуюся в непроводящей, нейтральной среде, в которой e = const, m = const (r = 0, j = 0). Если ось Х направить перпендикулярно к волновым поверхностям, то 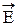и 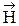( и их проекции на оси координат) не будут зависеть от координат У и Z.

Для описания электромагнитной волны в уравнениях

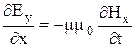, (20)

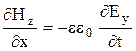, (21)

которые также получены из уравнений Максвелла, положим Е_х= H_y= 0.

Причем Е_х= H_х= 0, если отсутствуют постоянные, однородные электрические и магнитные поля.

Само волновое поле не имеет составляющей вдоль оси Х. Следовательно, векторы 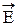и 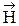перпендикулярны к направлению распространения волны, т. е. электромагнитные волны - поперечны.

При Е_х = Е_z = 0, Н_х = Н_у = 0, т. е. Е_у= Е, Н_z = Н.

Если электромагнитная волна распространяется вдоль одной оси Х, то

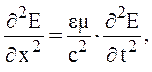
т. е. 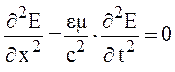. (22)

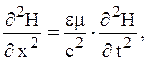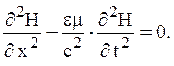т. е. (23)

Решениями уравнений (4.47) и (4.48) являются соответственно функции

Е = Е₀Cos (wt - kx + j₀₁), (24)

H = H₀Cos (wt - kx + j₀₂), (25)

где w - циклическая частота волны; k = 2p/l - волновое число; j₀₁ и j₀₂- начальные фазы электромагнитных волн в точке с координатой х = 0.

Из анализа уравнений (22), (23), (24) и (25) следует, что

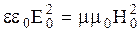. (26)

Следовательно, колебания магнитного и электрического векторов в электромагнитной волне происходят с одинаковой фазой (j₀₁= j₀₂ = j₀), одновременно обращаются в нуль и одновременно достигают максимума и минимума.

При наличии дисперсии скорость переноса энергии (групповая скорость) может отличаться от фазовой скорости.

Плотность потока энергии, переносимой электромагнитной волной, определяется вектором Пойнтинга 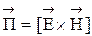, причем вектор 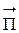совпадает с направлением распространения электромагнитной волны.

Дата добавления: 2016-02-09; просмотров: 1454;