Решетчатые функции, разности и суммы решетчатых функций

Сигналы в импульсных и цифровых системах подвергаются квантованию, поэтому воздействия в таких системах целесообразно рассматривать как дискретные или решетчатые функции.

Решетчатой функцией называется такая функция, значения которой определяются только при дискретных равноотстоящих друг от друга значениях независимой переменной; между этими значениями независимой переменной решетчатая функция равна нулю. Таким образом, решетчатые функции содержат информацию о соответствующей непрерывной функции лишь в дискретные моменты времени, определяемые периодом квантования, а при других значениях аргумента равны нулю.

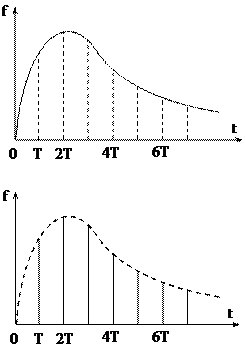Рис. 18.1. Решетчатая функция

На рис.18.1 показаны непрерывная функция f(t) и соответствующая ей решетчатая функция с периодом квантования Т, которая обозначается символом f(nT). Решетчатая функция f(nT) совпадает с исходной непрерывной функцией f(t) только в момент времени nT, где n – любое целое число. Ординаты решетчатой функции при значениях аргумента nt (n=0,1,2,…) называют дискретами. Например, непрерывной функции f(t)=sinwt соответствует решетчатая функция f(nT)=sinwnT, где Т – период прерывания, а n=0,1,2,¼

Каждой непрерывной функции f(t) можно привести в соответствие множество решетчатых функций, отличающихся периодом повторения или смешанных относительно друг друга.

Смешанные решетчатые функции имеют одинаковый период повторения Т, но сдвинуты относительно друг друга на интервал Dt, причем ôDtô£Т. Смещенная решетчатая функция записывается так:

,

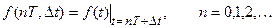а Dt может рассматриваться как некоторый параметр.

Очевидно, при Dt>0 смещенная решетчатая функция 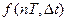сдвигается вправо относительно решетчатой функции f(nT) (здесь Dt=0), а при Dt<0 сдвиг происходит влево. При непрерывном изменении параметра Dt в интервале от 0 до Т решетчатая функция 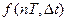становится тождественной исходной функции f(t).

Отметим, что решетчатая функция f(nT) не может однозначно определить соответствующую ей непрерывную функцию f(t) для всех значений независимой переменной, т.к. каждой решетчатой функции можно привести в соответствие множество непрерывных и разрывных функций, проходящих через ее дискреты в кратные периоду прерывания моменты времени (рис.18.2). Эти функции называют огибающими решетчатой функции. Простейшей огибающей можно рассматривать ступенчатую функцию.

Рис. 18.2. Огибающие решетчатой функции

Если период квантования T=const, то удобно перейти к новой независимой переменной, дискретные значения которой изменяются на единицу. Для этого необходимо аргумент t=nT функции f(nT) отделить от постоянного сомножителя Т. Например,

f(nT)=sinwnT, f(n)=sinw₁n, где w₁=wT, n=0,1,2,¼

Смещенная решетчатая функция при переходе к целочисленному аргументу обозначается f(n,a), где .

Например, для f(t)=sinwt имеем

,

где w₁=wT, , n=0,1,2,¼

Перейдем к рассмотрению разностных уравнений. Как известно, при исследовании непрерывных функций используются такие операции, как дифференцирование и интегрирование. Аналогами этих операций применительно к решетчатым функциям являются соответственно разности и суммы решетчатых функций.

Производным первого, второго и т.д. порядков для непрерывной функции по аналогии соответствует первая, вторая и т.д. разности для решетчатых функций. Разности решетчатых функций могут быть прямыми или обратными.

Первая прямая разность определяется так:

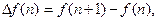
а первая обратная разность

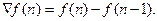
Эти разности показаны на рис.18.2.

Различие между прямой и обратной разностями решетчатой функции для момента времени t=nT заключается в том, что прямая разность находится по будущему значению решетчатой функции при t=T(n+1), а обратная разность – по прошлому значению решетчатой функции при t=T(n-1).

Вторые разности решетчатой функции определяются так:

прямая разность –

,

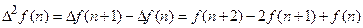обратная разность –

.

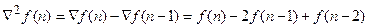В общем случае имеем:

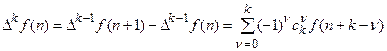; (18.1)

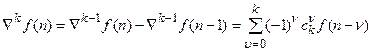, (18.2)

где 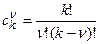- биномиальные коэффициенты (число сочетаний).

Сумма решетчатой функции 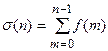является аналогом интеграла непрерывной функции в пределах от 0 до t.

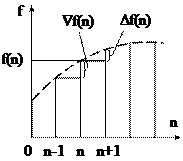Рис. 18.3. Прямые разности решетчатой функции

2. Понятие о разностных уравнениях

Разностные уравнения являются аналогом дифференциальных уравнений и служат для описания динамических процессов в дискретных системах.

Неоднородное разностное уравнение (уравнение в конечных разностях) через прямые разности может быть записано так:

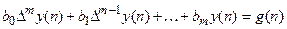, (18.3)

где g(n) – заданная, а y(n) – определяемая решетчатые функции.

При 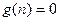уравнение (18.3) становится однородным.

Учитывая (18.1), уравнение (18.3) можно представить так:

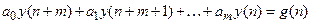, (18.4)

где связь между коэффициентами уравнений (18.3) и (18.4) имеет вид

.

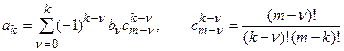Неоднородное разностное уравнение через обратные разности может быть записано следующим образом:

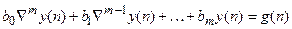, (18.5)

Учитывая (18.2), уравнение (18.5) принимает вид

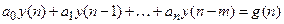, (18.6)

где связь между коэффициентами уравнений (18.5) и (18.6) выражается так:

.

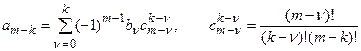При решении разностных уравнений (18.4) их можно рассматривать как рекуррентные соотношения для вычисления значения y(n+m) при n=0,1,2,¼ , если заданы начальные значения y(0), y(1), ¼, y(m-1). Аналогично по уравнению (18.6) можно определить значения y(n) при n=0,1,2,¼ для заданных начальных значений y(n-m), y(n-m-1), y(n-1). Схема этих вычислений весьма проста и для переменных во времени коэффициентов b_i,a_i (i=0,1,2,¼).

Рассмотрим решение однородного разностного уравнения

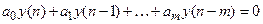. (18.7)

Этому разностному уравнению соответствует характеристическое уравнение

.

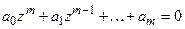Если через z_i (i=1,2,¼ ,m)обозначить корни этого характеристического уравнения (полагаем, что кратные корни отсутствуют), то общее решение однородного разностного уравнения (18.7) имеет вид

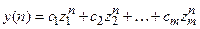, (18.8)

где c_i (i=1,2,¼,m) - произвольные постоянные.

Процесс (18.8) будет затухающим (при 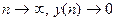), если будет выполнено условие 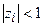(i=1,2,¼ ,m).

3. Дискретное преобразование Лапласа. Z-преобразование

Как и для непрерывных функций, при операциях над дискретными функциями используется преобразование Лапласа. Это преобразование, в отличие от обычного, называют дискретным преобразованием Лапласа.

Дискретное преобразование Лапласа для решетчатой функции f(nT) обозначается через F^*(p) и определяется таким образом:

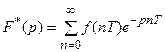, (18.9)

Для смещенной решетчатой функции f(n,T,Dt) получаем

.

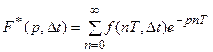Если решетчатые функции представлены в виде f(n), f(n,a), то для них соответственно имеем:

,

,

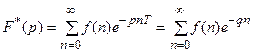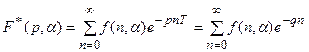где q=pT.

Рассмотрим вспомогательную дискретную функцию f^*(nT), которая выражается через исходную непрерывную функцию f(t) следующим образом:

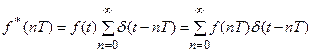. (18.10)

Эта функция представляет собой дискретную последовательность из единичных импульсных функций (d-функций), взятых с коэффициентами, равными значениям исходной непрерывной функции f(t) в соответствующие моменты времени nT (n=0,1,2,¼).

Найдем теперь преобразование Лапласа от этой (16.10) дискретной функции :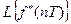

.

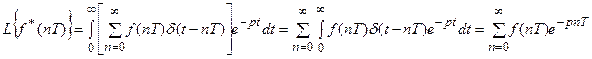Таким образом, преобразование Лапласа от дискретной импульсной функции (18.10) полностью совпадает с дискретным преобразованием Лапласа от соответствующей решетчатой функции.

Z-преобразование. При исследовании дискретных систем широкое применение получило z-преобразование, которое может быть получено из дискретного преобразования Лапласа (18.2) путем подстановки .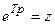

Таким образом, выражение для z-преобразования решетчатой функции f(nT), обозначаемое через 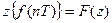, имеет вид

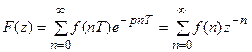. (18.11)

Соответственно для смещенной решетчатой функции f(n,a) получаем так называемое модифицированное (смешанное) z-преобразование

.

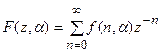Выражение для z-преобразования могут быть записаны и для непрерывных функций:

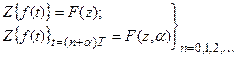
Рассмотрим без доказательства основные теоремы z-преобразования.

Теорема линейности

Если функции 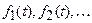имеют соответственно z-преобразования 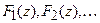, то

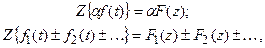
где a - постоянная величина.

Теорема сдвига по временной области

Если 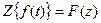, то .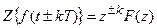

Теорема смещения независимого переменного

(умножение оригинала на экспоненту)

,

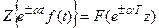где a - положительное число, а 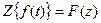. Следовательно, умножение функции f(t) во временной области на экспоненциальную функцию 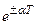приводит в z-области к изменению масштаба независимой переменной в 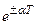раз.

Теорема о конечном значении

Если 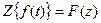не содержит полюсов на окружности единичного радиуса или вне ее, то

.

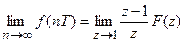Эта теорема позволяет определить установившееся значение любой переменной дискретной системы по соответствующему z-преобразованию.

Теорема о начальном значении

Если 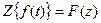, то .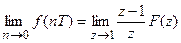

Найдем теперь z-преобразование некоторых характерных функций.

1. Ступенчатая функция 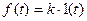. Соответствующая решетчатая функция имеет вид 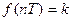, далее находим

.

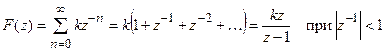2. Функция с постоянным наклоном 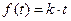. Имеем 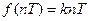, находим z-преобразование этой функции

.

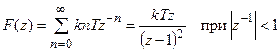3. Экспоненциальная функция 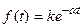. Имеем 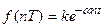, тогда получаем

.

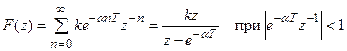4. Разности решетчатых функций. Для первой прямой разности имеем

.

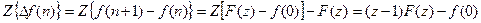Если рассмотреть 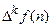, то получим

,

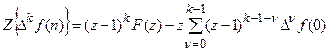причем 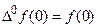. При условии f(0)=f(1)=f(2)=¼=f(k-1)=0 полученное выражение упрощается

.

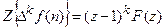Для первой обратной разности находим

.

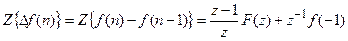Если для отрицательных аргументов решетчатая функция равна нулю, то получаем

.

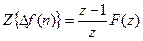Для k-ой обратной разности при f(n)=0 при n<0 будем иметь

.

5. Суммы решетчатых функций. Для неполной суммы имеем , тогда z-преобразование от этого выражения может быть представлено

.

Для полной суммы будем иметь

.

z-преобразование типовых функций изображены в табл. 18.1.

Таблица 18.1

z-преобразование функций времени

№ №	Оригинал F(t)	Преобразование Лапласа Fл(p)	z-преобразование F(z)	Модифицированное z-преобразование F(z,s)
	1(t)
	t