Глава 2. Восстановление работоспособного состояния машин
2.1. Стратегии восстановлений
Поддерживание оборудования в работоспособном состоянии требует определенных материальных и трудовых затрат. Уровень этих затрат во многом определяется принятой стратегией восстановления работоспособного состояния машин.
Под стратегией восстановления понимается определенная периодичность замен и уровень восстановления работоспособного состояния. Будем различать минимальное и полное восстановления. Минимальное восстановление подразумевает минимум затрат на устранение отказа.
Термин «стратегия восстановления» применим как к агрегату или машине в целом, так и к ее составным частям. Применительно к агрегату (машине) полное восстановление реализуется при капитальном ремонте, минимальные восстановления – при текущих ремонтах.
При текущих и аварийных ремонтах машин восстановление их работоспособного состояния может осуществляться либо заменой составной ее части (механизм, узел), в которой произошел отказ, либо заменой (восстановлением) непосредственно отказавшей детали. Тогда, применительно к механизму (узлу), в первом случае используется термин «полное восстановление», во втором случае – термин «минимальное восстановление», а термин «стратегия восстановления» будет относится непосредственно к механизму (узлу).
Например, в соединении вал – зубчатое колесо заменяется отказавшая шпонка. В этом случае при замене шпонки происходит восстановление работоспособности узла, но не обеспечиваются исходные показатели надежности узла. Восстановление исходных показателей надежности предполагается при полной замене узла, т.е. при полном восстановлении исходных показателей надежности узла.
В процессе эксплуатации металлургического оборудования требуется обеспечить минимум затрат на поддержание оборудования в работоспособном состоянии.
2.2. Стратегии восстановлений при внезапных отказах
Как правило, металлургические агрегаты являются агрегатами непрерывного действия и большой производительности. Любой отказ связан с большими потерями. Поэтому основой надежной работы оборудования являются периодические остановки на профилактическое техобслуживание и ремонты. В таких ситуациях главной проблемой является планирование объема ремонтных работ, т.е. какие узлы, детали менять в тот или иной ремонт, или не менять, обеспечивая готовность замены в любой момент.
В качестве критерия для оценки стратегий восстановлений принимается интенсивность затрат (средние затраты на восстановление в единицу времени).
Рассмотрим возможные стратегии восстановлений применительно к оборудованию металлургических заводов.
Стратегия аварийных замен (стратегия - 1)
Система восстанавливается полностью только после отказа. После полного восстановления показатели надежности системы соответствуют ее исходному состоянию.
 l1 l2 l3 ln
l1 l2 l3 ln
t1 t2 t3 tn t
Рис.2.1. Схема стратегии аварийных замен:
t1, t2, t3 и tn – моменты отказов;
l1, l2, l3 и ln – наработки;
· - полное восстановление
Для данного случая интенсивность затрат R определяется из зависимости:
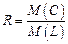 , (2.1)
, (2.1)
где M(C) - математическое ожидание эксплуатационных затрат в Ci - м цикле;
M(L) - математическое ожидание наработок, имеющих протяженность Li.
Стратегия плановых и аварийных полных замен (стратегия - 2)
Система в случае отказа подвергается полному аварийному восстановлению, а в фиксированные моменты времени
ti=t, 2t, … nt проводятся плановые замены.
 |
t 2t nt t
Рис.2.2. Схема стратегии – 2
Обозначим через Сn и Са затраты, связанные соответственно с плановыми и аварийными заменами, тогда интенсивность эксплуатационных затрат:
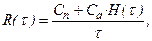
где H(t) – математическое ожидание числа аварийных восстановлений на интервале [0, t].
Оптимальный межремонтный период:
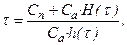
где h(t) = H′(t) – плотность восстановлений.
Если существует оптимальный межремонтный период t*, то минимальная интенсивность эксплутационных затрат:
R(t*) = h(t*)
Стратегия полных плановых и аварийных минимальных замен
(стратегия - 3)
Система в моменты времени ti=t, 2t, … nt планово восстанавливается полностью. В случае отказа в межремонтный период осуществляется минимальное восстановление системы.
Примем затраты на полное восстановление - Сп, затраты на минимальное восстановление – Са .
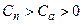 .
.
 |
t 2t nt t
 – минимальное восстановление
– минимальное восстановление
Рис. 2.3 . Схема стратегии –3
В среднем на календарный цикл [0,t] приходится l(t) минимальных восстановлений, определяемых из зависимости:
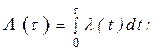
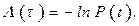
Поэтому интенсивность затрат:
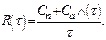 (2.2)
(2.2)
Тогда оптимальный интервал восстановления 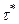 из условия
из условия 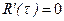 определяется уравнением:
определяется уравнением:
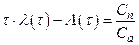 . (2.3)
. (2.3)
Если 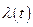 - интенсивность отказов – возрастающая функция, то
- интенсивность отказов – возрастающая функция, то
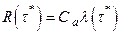 . (2.4)
. (2.4)
Так, для распределения Вейбулла:
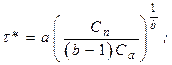 (2.5)
(2.5)
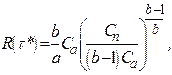 (2.6)
(2.6)
где b – параметр формы;
a – ресурсная характеристика.
Пример 2.1. Наработка редуктора имеет распределение Вейбулла
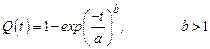
с параметрами a=90 сут, b=2.
Затраты на полную замену Cn=12 ед., на минимальную замену Cа=6 ед (условие 1) .
Найти оптимальный интервал профилактических замен и соответствующую ему интенсивность затрат.
Решение.
Находим оптимальный интервал из зависимости (2.5).
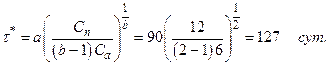
Для заданных условий (1) по зависимости (2.6) находим интенсивность затрат.
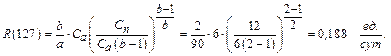
Установим, как изменяется ситуация с изменением параметров распределения Вейбулла и соотношения затрат на минимальное и полное восстановления.
Условие 2. Примем b=3 при низменных затратах, тогда:
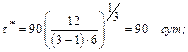
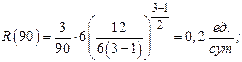
Получаем возрастание интенсивности затрат.
Условие 3. Для b=2 и Ca=3 ед., получим:
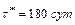
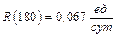
Условие 4. Для b=3 и Ca=3 ед., получим:
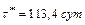
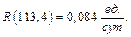
Более эффективным является снижение затрат на минимальное восстановление.
Сравним для заданных условий эффективность стратегий 3 и 1.
Для стратегии аварийных полных замен b=2, C=12 ед.:
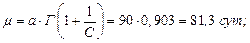
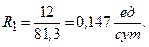
для b=3, C=12 ед.:
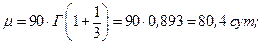
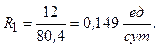
Таким, образом для условий 1 и 2 более эффективной является стратегия аварийных замен, так как
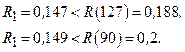
Для условий 3 и 4 более эффективна стратегия 3, так как
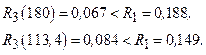
То есть применение той или иной стратегии восстановления работоспособности оборудования определяется характером распределения и соотношения затрат на полные и минимальные восстановления.
Стратегия аварийных минимальных замен (стратегия -4)
Система после первых (n-1) отказов подвергается минимальному восстановлению. После n-го отказа система восстанавливается полностью
 xn
xn
1 2 n t
Рис. 2.4 . Схема стратегии – 4
Интенсивность эксплуатационных затрат:
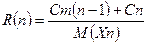 , (2.7)
, (2.7)
где Cm, Cn - средняя стоимость минимальных и соответственных полных восстановлений;
M(Xn) - математическое ожидание длины цикла.
Для распределения Вейбулла оптимальное число минимальных восстановлений:
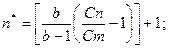 (2.8)
(2.8)
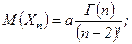 (2.9)
(2.9)
где 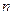 =1, 2 …,
=1, 2 …,
тогда
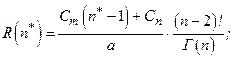 (2.10)
(2.10)
Пример 2.2. Замена комплекта вкладышей универсального шпинделя составляет 300 ед. (минимальное восстановление). Полное восстановление путем замены шпинделя в сборе 12000 ед.
Наработка комплекта вкладышей имеет распределение Вейбулла с параметрами a=60 сут, b=4.
Определить оптимальное число минимальных восстановлений и соответствующую этому интенсивность эксплуатационных затрат.
Решение:
Находим оптимальное число восстановлений
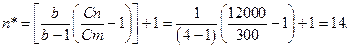
Тогда минимальная интенсивность эксплуатационных затрат составит:
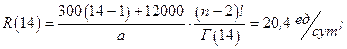
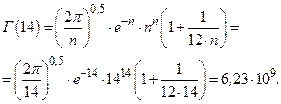
Длительность интервала полных замен:
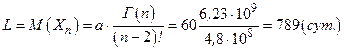
2.3. Восстановление при постепенных отказах
В отличие от внезапных отказов, начинающиеся постепенные отказы можно распознать при наблюдении за параметрами, определяющими работоспособность системы, и предотвратить их в дальнейшем соответствующими восстановительными мероприятиями.
В ряде случаев планирование восстановительных работ можно осуществлять не на основе допустимой величины параметра, определяющего работоспособность системы (например, допустимая величина износа), а на основе текущих затрат на восстановление.
Если текущие затраты на восстановление неоправданно велики, то можно говорить о постепенном отказе. Поэтому необходимо найти наиболее выгодное в отношении затрат время эксплуатации (время от ввода системы в действие до ее снятия с эксплуатации).
Обозначим через A (t) средние затраты на восстановление, которые возникают за время (0,  ). То есть предполагается, что одновременно эксплуатируются несколько однотипных систем (группа прессов, волочильных станов, мостовые краны и т.д.).
). То есть предполагается, что одновременно эксплуатируются несколько однотипных систем (группа прессов, волочильных станов, мостовые краны и т.д.).
Если функция А (t) растет линейно А (t) = a t, то с точки зрения затрат нет необходимости производить полное восстановление (замена системы), так как удельные затраты на восстановление остаются постоянными:
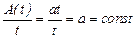 .
.
Если длина цикла - 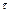 , а затраты на восстановление (замену системы) — с, тогда интенсивность эксплуатационных затрат
, а затраты на восстановление (замену системы) — с, тогда интенсивность эксплуатационных затрат
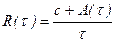 . (2.11)
. (2.11)
Если же функция А (t) растет быстрее, чем линейно (то есть изменение средних затрат d A(t)= a (t) d t, то может оказаться экономичнее заменить систему на новую.
Тогда экономичное время эксплуатации 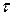 , определенное соотношением:
, определенное соотношением:
R ( 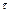 *) =min R (т),
*) =min R (т), 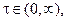
является решением уравнения 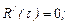
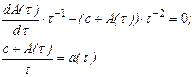
и тогда
R( 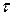 )=a(
)=a( 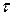 ). (2.12)
). (2.12)
Кривая эксплуатационных затрат описывается выражением
T (t) = C+A (t) = C + 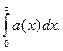 (2.13)
(2.13)
Согласно выражению (2.10) для 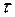 =
= 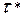
С + А( 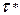 ) = а (
) = а ( 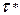 )
) 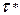
прямая у = а ( 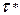 )t касается кривой эксплуатационных затрат, что определяет экономичное время эксплуатации
)t касается кривой эксплуатационных затрат, что определяет экономичное время эксплуатации 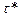 (рис. 2.5).
(рис. 2.5).
Если принять, что а (t) = a t, а > 0 (что, как показывает практический опыт, во многих случаях соответствует действительности), тогда в соответствии с уравнением (2.10)
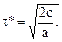 (2.14)
(2.14)
Соответствующая минимальная интенсивность эксплуатационных затрат:
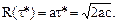 (2.15)
(2.15)
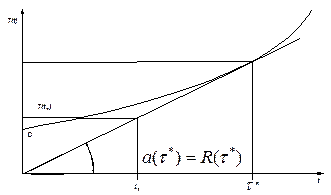
Рис.2.5. Экономичное время эксплуатации
Пример 2.3. Средние затраты в единицу времени на замену вкладышей в линии привода группы чистовых клетей стана 2500 г/п а (t) = 6 ед./сут, полная замена шпиндельного соединения
С = 12000 ед. Средняя наработка вкладышей Т=60 сут.
Определить экономичное время эксплуатации и соответствующую интенсивность эксплуатационных затрат.
Решение:
В соответствии с формулами (2.14) и (2.15)
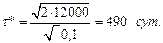
a = a (t) / T = 6 / 60 = 0,1;
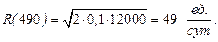
Общие затраты T = 490 ·49 = 24010 ед.
2.4. Восстановление на основе задания лимита затрат
Стратегия экономичного времени эксплуатации отражает динамику средних затрат на восстановление А (t) в рассматриваемой совокупности систем. Однако текущие затраты на восстановление конкретных систем часто заметно отличаются друг от друга из-за различных условий эксплуатации (рис.2.6).

Рис. 2.6. Стратегия задания лимита затрат на восстановление
Для учета специфики каждой системы применяется методика с ограничением затрат на восстановление.
Сначала оцениваются затраты на восстановление. Если они превышают заданную границу - лимит затрат на восстановление, то система не восстанавливается, а заменяется.
Тогда интенсивность эксплуатационных затрат есть величина постоянная для используемой стратегии:
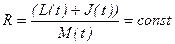 . (2.16)
. (2.16)
Из уравнения (2.14) лимит затрат на восстановление
L (t) = R ·M (t) – J (t).
Если затраты на восстановление на интервале (0,t)
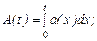
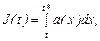 0 < t <
0 < t < 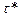 ;
;
M (t) = 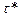 - t, 0 < t <
- t, 0 < t < 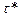 ,
,
тогда лимит затрат на восстановление
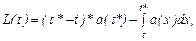
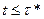 .
.
При линейной зависимости а (t) = at с учетом формул (2.12) и (2.13)
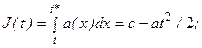
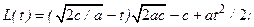
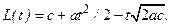 (2.17)
(2.17)
Пример 2.4. Определить, требуется ли в момент времени t=400 сут восстановление линии привода путем замены комплекта вкладышей или необходима замена шпинделя в сборе. Исходные данные примера 2.3.
Решение.
Определим из зависимости (2.17) лимит затрат на восстановление
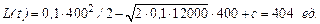
Восстановление должно производиться путем замены комплекта вкладышей, так как затраты на их замену составляют 360 ед., что меньше лимита L(t)=404 ед.
2.5. Оценка эффективности принимаемых решений
при техническом обслуживании
Работоспособность оборудования в конечном итоге должна обеспечивать его эффективную работу, приносить доход. Поэтому необходим и анализ потерь, снижающих эффективность работы оборудования.
Такими критериями являются:
- простои из-за отказов оборудования;
- ремонтные и монтажные работы;
- незначительные остановки оборудования;
- технологические недоработки;
- сокращение скорости технологического процесса;
- сокращение доходов.
В общем виде предельная эффективность (ПЭ) оборудования может быть представлена уравнениями Накаямы:
ПЭ = Готовность ·Производительность ·Качество.
Готовность выражается через коэффициент готовности Кг:
Кг = (Рабочее время - Время простоя) / Рабочее время.
Производительность – через темп производства (ТП), как произведение нормы эксплуатации (НЭ) на норму скоростной эксплуатации (НСЭ).
ТП = НЭ ·НСЭ.
НЭ = 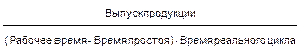 ,
,
где  – время на производство единицы продукции.
– время на производство единицы продукции.
НСЭ = 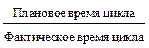 .
.
Качество выражается через коэффициент качества Кк:
Кк = 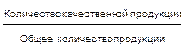 .
.
Из анализа представленных зависимостей можно сделать следующие выводы.
Уровень готовности определяют два первых вида потерь (простои из-за отказов оборудования, ремонтные и монтажные работы).
Уровень производительности определяется остановками оборудования и скоростью технологического процесса.
В понятие качества входят потери, связанные с технологическими недоработками и сокращением доходов, вызванных снижением качества продукции.
Для оценки эффективности решений, связанных с техническим обслуживанием оборудования, существует обобщенный показатель – так называемая интегральная шкала эффективности (ИШЭ), предложенная Хиби:
ИШЭ = 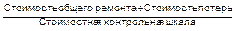
В качестве стоимостной контрольной шкалы используется стоимость энергии (кВт ·ч) или другие измеряемые показатели.
В развернутом виде формула ИШЭ = U за i-й период:
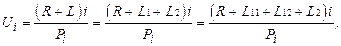
где U 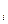 - интегральная шкала эффективности за i-й период;
- интегральная шкала эффективности за i-й период;
R - стоимость ремонта;
L - потери при отказе оборудования;
L1 - потери продукции;
L11 - предотвращение потерь в результате снижения
производительности;
L12 - уменьшение потерь действующей продуктивности;
L2 - стоимость потерь;
Pi - стоимость контрольной шкалы за i-й период.
Следовательно, для оценивания эффективности мероприятий необходимо постоянно осуществлять мониторинг состояния оборудования и затрат на поддержание его работоспособного состояния.
Дата добавления: 2015-12-11; просмотров: 3292;
