Роль науки о механике сплошной среды

Для решения задачи по разработке и транспортировке углеводородов с широким внедрением достижений науки и техники при кардинальном ускорении научно-технического прогресса, успешного и эффективного роста темпов и объемов буровых работ и ведения повсеместного снижения затрат времени и средств на строительство скважин, предупреждение и ликвидацию аварий на них. Использование накопленного объема практических и теоретических сведений о закономерностях разрушения горных пород и транспортировки выбуренной породы на поверхность, гидравлических потерях в скважине и поглощениях бурового раствора, об устойчивости стенок скважин и прочности крепи. Все основные и сопутствующие процессы здесь механического происхождения.

С позиции механики буровой и цементные растворы, горные породы и содержащиеся в них флюиды, материал, из которого изготовлены бурильные и обсадные трубы - сплошные среды. Поэтому их движение, деформирование, устойчивость и разрушение изучаются на основе законов гидродинамики, теории фильтрации, теории упругости, механики разрушения и других разделов механики сплошной среды.

В настоящее время публикуется много статей, обзоров и монографий, посвященных частным задачам и отдельным разделам механики сплошной среды. Инженерам и научным сотрудникам, работающим в бурении, разработке и транспортировке нефтепродуктов и газодобыче бывает трудно без специальной подготовки разобраться в основных положениях, уравнениях, формулировках и решениях разного рода задач механики.

Задача состоит не только в овладении накопленными знаниями и использовании их на практике, но и в дальнейшем развитии наших представлений о процессах, происходящих в недрах и на поверхности.

Академик Л. И Седов отмечал, что в науке и технике от глубины проникновения в суть дела, от учета многих привходящих обстоятельств, от надежности и достоверности различных предложений могут зависеть устранение серьезных потерь и рационализация больших материальных затрат.

Механика сплошной среды — наука о движении газообразных, жидких и твердых деформируемых тел. Наша задача - показать, как формулируются и решаются различные по характеру и сложности инженерные задачи бурения и разработки нефтяных и газовых месторождений.

Газ, жидкость, твердое деформируемое тело рассматриваются как среда, непрерывно (сплошным образом) заполняющая часть пространства, занятого телом, которое является сплошным непрерывным континуумом. Это идеализация необходима для использования аппарата математического анализа.

Механика сплошной среды возникла в связи с решением таких простейших задач, как установление закономерностей истечения жидкостей из сосудов, просачивания жидкости через грунт, прогиба балок, находящихся под нагрузкой и рассматриваются движения тел с изменяющимися расстояниями между точками во время движения.

Исследование таких частных задач привело к формулировке основных законов движения и равновесия сплошной среды. С течением времени перед механикой сплошной среды возникали более трудные задачи, решение которых требовали особого накапливания и концентрации опыта, специальных методов теоретических и экспериментальных исследований. Все это и привело к созданию и развитию механики сплошной среды как науки.

В настоящее время механику сплошной среды разделяют на две крупные области: механику жидкости и газа (гидромеханика) и механику твердых деформируемых тел.

Гидромеханика включает в себя следующие основные разделы: 1) механика идеальной жидкости, 2) механика вязкой, или ньютоновской, жидкости, 3) механика невязкой, или неньютоновской, жидкости, 4) механика турбулентных течений. К гидромеханике непосредственно примыкают механика фильтрационных течений и ряд других технических разделов механики.

Механика деформируемых тел состоит из следующих основных разделов: а) теория упругости, б) теория пластичности, в) теория ползучести, г) механика сыпучих тел, к которым непосредственно примыкают теория прочности и механика разрушения.

Такое разделение механики сплошной среды связано с тем, что различные тела даже при одних и тех же внешних условиях ведут себя по-разному. Поэтому определяющие процесс параметры и функции, граничные условия и дифференциальные уравнения также не одинаковы.

Математическое описание, или, построение, математической модели движения какой-либо сплошной среды основано на фундаментальных законах ньютоновской механики, законах термодинамики, экспериментальных уравнениях состояния. Основными законами механики, справедливыми для любого индивидуального объема всякой сплошной среды, служат закон сохранения массы и закон сохранения количества движения.

Если рассматривать сплошную среду как термодинамическую систему, для которой определены не только механические понятия о положении и движении, но и физические понятия о внутреннем состоянии, то следует использовать первый и второй законы термодинамики. Основные термодинамические характеристики физических тел: температура, тепловой поток, теплопроводность, представляющие как самостоятельный интерес, так и в связи с их влиянием на механические характеристики процесса, рассматриваются по мере необходимости.

Уравнения состояния, получаемые на базе экспериментального изучения свойств материалов, являются связью между параметрами, определяющими механическое поведение конкретной сплошной среды в конкретных условиях внешнего воздействия.

Введем основные понятия, общие уравнения и соотношения, которыми пользуются в механике сплошной среды, используя работы Л. И. Седова, Н. И. Мусхелишвили, Л. Г. Лойценского и других известных ученых.

§ 1. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ

Общая задача кинематики — описание движения среды безотносительно к тому, какие внешние условия вызывают и поддерживают данное движение. Так как сплошная среда представляет собой непрерывную совокупность точек, то определить движение среды — значит описать движение всех ее точек. Движение всегда определяется по отношению к некоторой системе отсчета - системе координат. Условимся через x₁_, х₂, х₃ обозначать координаты любой ортогональной системы координат, если нет специальной оговорки.

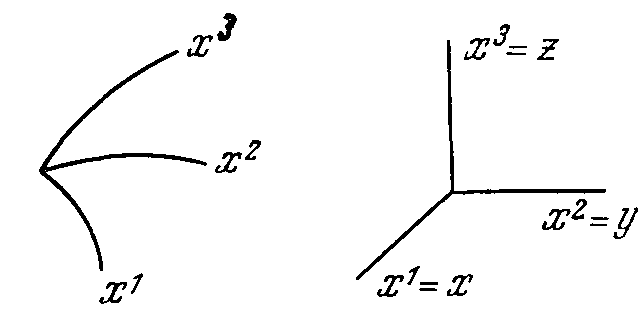
Рис. 1

Существуют два исторически сложившихся способа задания движения. Первый из них, связанный с именем Лагранжа, заключается в задании кинематических уравнений движения:

x_i= x_i (ξ₁, ξ₂, ξ₃, t) (i = 1. 2, 3), (1.1)

где ξ_i - являются координатами фиксированной (или индивидуальной) точки среды. Совокупность величин ξ_i и t называют переменными Лагранжа.

Основная задача механики сплошной среды заключается в определении закона движения (1.1). Построение математической модели любой сплошной среды явно или неявно опирается на понятие закона движения.

При лагранжевом задании движения проекции скоростей 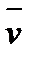и ускорений 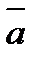точек среды на оси координат х_i, определяются обычными равенствами

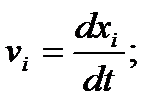
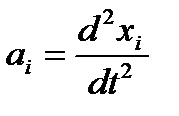. (1.2)

Хотя лагранжев способ и применяется в некоторых задачах механики сплошных сред, все же он уступает другому, более широко используемому способу Эйлера, который заключается в задании перемещений и, скоростей v, ускорений а и других интересующих нас величин как функций координат точек пространства х_i и времени t, т. е.

u_i = u_i(x₁, x₂, x₃, t);

v_i = v_i(x₁, x₂, x₃, t);

a_i = a_i(x₁, x₂, x₃, t). (1.3)

Совокупность параметров х_j и t называют переменными Эйлера.

Основное различие между методами Лагранжа и Эйлера состоит в том, что с точки зрения Лагранжа нас интересуют законы изменения положения, скорости, ускорения и других величин данной индивидуальной точки сплошной среды, а с точки зрения Эйлера — перемещение, скорость, ускорение и т. д. в точке пространства, мимо которой в данный момент проходят частицы среды.

В механическом отношении оба способа эквивалентны.

При необходимости можно совершить переход от переменных Лагранжа к переменным Эйлера, и наоборот. Если известен закон движения сплошной среды в форме Лагранжа, то, чтобы выразить его в форме Эйлера, достаточно разрешить уравнения (1.1) относительно ξ_i, т. е. получить

ξ_i= ξ_i(x₁, x₂, x₃, t) (1.4)

Эти соотношения при фиксированных координатах х_j указывают те точки ξ_i сплошной среды, которые в разные моменты времени проходят через данную точку пространства.

Если в формулы для проекции скоростей v_i= v_i(ξ₁, ξ₂, ξ₃, t)идругих величин, заданных с точки зрения Лагранжа, подставить соотношения (1.4), то будут найдены функции в переменных Эйлера х_j и t.

В том случае, когда задано распределение скорости в форме Эйлера (1.3), учитывая равенства (1.2), получим систему обыкновенных дифференциальных уравнений относительно х_i:

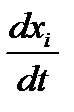= v_i(x₁, x₂, x₃, t) (i = 1, 2, 3).

Решив эту систему, найдем x_j = x_j(C₁, C₂, C₃, t), где С₁, С₂, С₃ — постоянные, определяемые по х_j, при t = t₀, т. е. они являются координатами индивидуальной точки сплошной среды (переменными Лагранжа).

При изучении движения сплошной среды широко используют понятие поля скалярной и векторной величин. Совокупность значений той или иной величины, заданной в каждой точке рассматриваемой области, называется ее полем.

Если рассматриваемая величина—скаляр (давление р, плотность ρ, температура T и т.д.), то поле называется скалярным; если же — вектор (перемещение 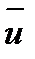, скорость 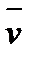, ускорение 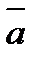и т. д.), то поле называется векторным.

Как скалярная, так и векторная величины не зависят от выбранной системы координат. Так как вектор определяется тремя числами (компонентами или проекциями на оси координат), то векторное поле равнозначно трем скалярным полям. Однако эти поля уже зависят от системы координат.

На примере поля плотности ρ и поля скоростей 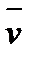рассмотрим некоторые общие характеристики полей.

Поле ρ = ρ(х_1; х₂, х₃), характеризующее данный процесс или движение, может быть стационарным dρ/dt=0 (установившимся) или нестационарным dρ/dt≠0 (неустановившимся). Одно и то же движение может быть как установившимся, так и неустановившимся, все зависит от выбора системы координат, относительно которой изучается движение. Поэтому говорят, что установившееся (стационарное) движение — понятие относительное.

Если распределение плотности задано с точки зрения Лагранжа ρ = ρ (ξ₁, ξ₂, ξ₃, t), то определить изменение плотности частицы сплошной среды очень просто, оно равно (dρ/dt)_ξi. Сложнее, когда ρ = ρ(x_l, x₂, x₃, t), т.е. функция задана в переменных Эйлера. В этом случае необходимо перейти от переменных Эйлера к переменным Лагранжа и воспользоваться правилом дифференцирования сложной функции, что приведет к формуле

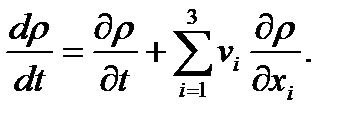(1.5)

Производная dρ/dt характеризует изменение плотности данной частицы сплошной среды в единицу времени и называется индивидуальной, субстанциональной или полной производной. Производная ∂ρ/∂t характеризует изменение плотности в данной точке пространства в единицу времени и называется местной или локальной. Сумма 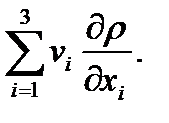— в правой части (1.5) называется конвективной производной.

Аналогично формуле (1.5) можно написать формулы для определения полной производной по времени проекций любой векторной величины, заданной в переменных Эйлера. Например, ускорение частицы сплошной среды в проекциях на оси декартовой системы координат имеет вид

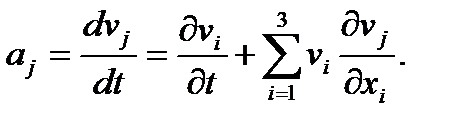(j = 1, 2, 3) (1.6)

а в проекциях на оси цилиндрической системы координат rΘz при осевой симметрии будет

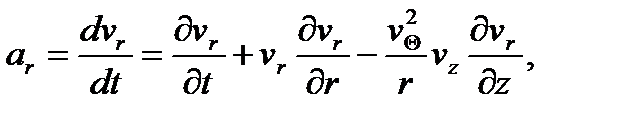
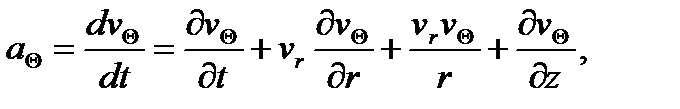(1.6*)

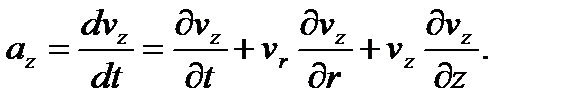
Для любого векторного поля используют понятие векторных линий. Векторные линии— это семейство линий, касательные к которым совпадают с направлением вектора.

В случае поля скоростей эти линии называются линиями тока.

Если выбрать произвольную кривую С, не совпадающую с линией тока, и через каждую ее точку провести линию тока, то образуется поверхность тока. Если кривая С замкнута, поверхность тока называется трубкой тока.

4-09-2014

Аналитически семейство линий тока можно найтииз условия коллинеарности элемента 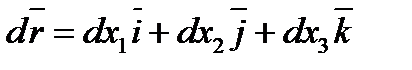, взятого вдоль линии тока, и вектора скорости 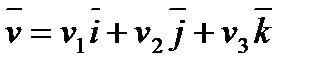,т.е.

НБб-09=7.02

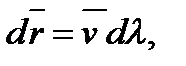или в проекциях

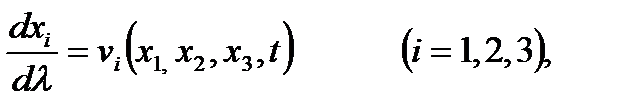(1.7)

где dλ— скалярный параметр. Это и есть дифференциальные уравнения линий тока. Они отличаются от уравнений, описывающих закон движения или траектории движения частиц сплошной среды

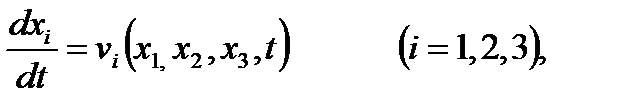(1.8)

тем, что в уравнениях (1.7) t — параметр, а в уравнениях (1.8) t — переменная величина.

Таким образом, линии тока не совпадают с траекториями. Они совпадают только при движениях установившихся (так как в этом случае между уравнениями (1.7) и (1.8) нет различия) и при неустановившихся, когда поле скоростей изменяется по величине, но не изменяется по направлению.

Если задана плотность (или любая другая скалярная величина, например Т- температура) как функция переменных Эйлера, то в каждый момент времени можно рассматривать поверхность

T(x₁,x₂,x₃,t)=const, (1.9)

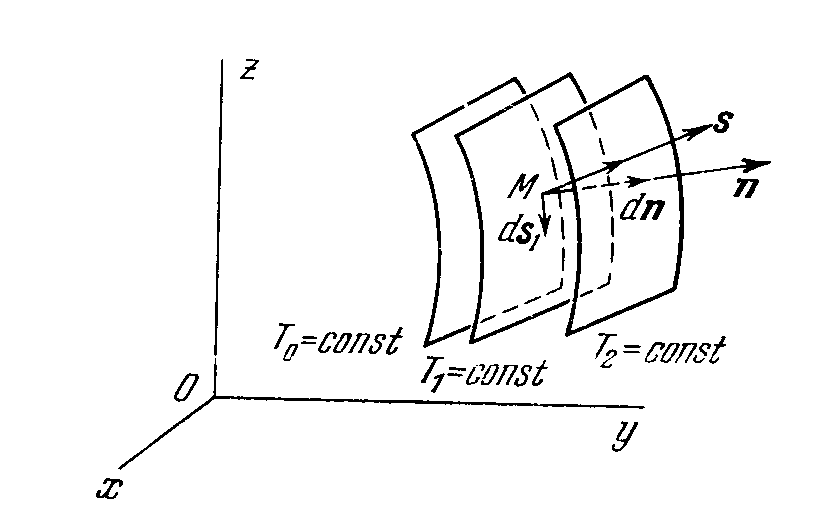
которая называется поверхностью равного уровня или эквипотенциальной.

Рис. 2 Поверхности равного уровня.

Вектор, направленный по нормали 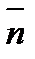в какой-либо точке М поверхности (1.9) в сторону роста T и равный по величине 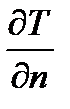, называется вектором-градиентомскалярной функции Tв точке М. Он обозначается и вычисляется так:

,

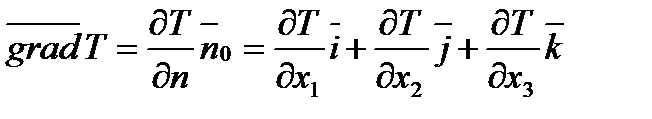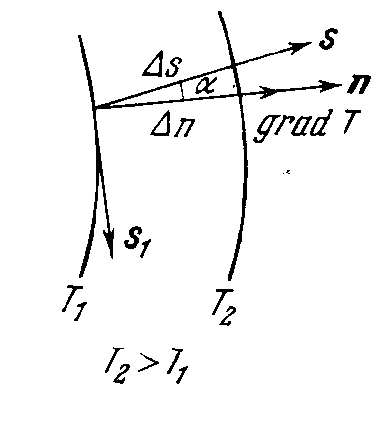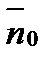где и 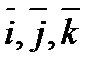— единичные векторы по направлению 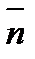и вдоль координатных осей.

Проекция вектора grad T на некоторое направление 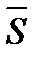определяет изменение температуры в этом направлении:

,

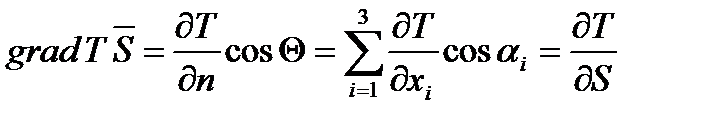где Θ — угол между направлениям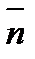и и 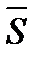; cosα_i — направляющие косинусы вектора .

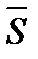Рис.3 Вектор – градиент температуры

Наибольшее изменение плотности происходит в направлении, нормальном к поверхности (1.9).

Если в поле скорости 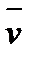(или любой другой векторной величины) мысленно провести некоторую поверхность S и в каждой ее точке задать нормаль 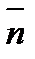, то для определения объема жидкости, протекающей за единицу времени сквозь поверхность S, необходимо вычислить интеграл

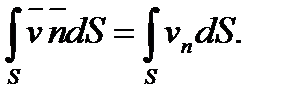
Этот интеграл называется потоком скоростичерез поверхность S. Поток скорости сквозь замкнутую поверхность S, отнесенный к единице объема V, заключенного внутри S, называется расхождениемили дивергенциейскорости, т. е.

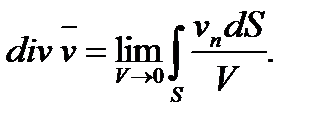
В декартовой системе координат дивергенция скорости вычисляется по формуле

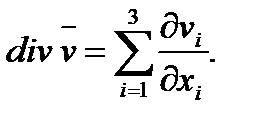
Видно, что дивергенция скорости определяет скорость объемного расширения жидкости в бесконечно малой окрестности данной точки. Поэтому поток скорости через замкнутую поверхность S должен быть равен расширению всего объема V жидкости внутри S, т. е.

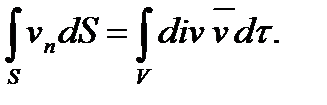(1.10)

Это равенство называется формулой Гаусса.

Если в поле 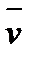мысленно проведен какой-либо замкнутый контур L, ограничивающий некоторую поверхность S, то линейный интеграл

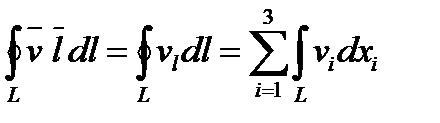
называется циркуляцией скорости, а вектор, определяемый в виде

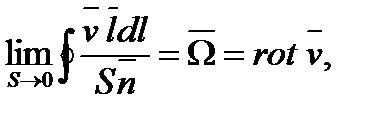
называется вихремили ротором скорости. Здесь 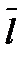, 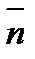— единичные векторы, направленные соответственно по касательной к L и по нормали к поверхности S.

В декартовой системе координат вихрь скорости вычисляется по формуле

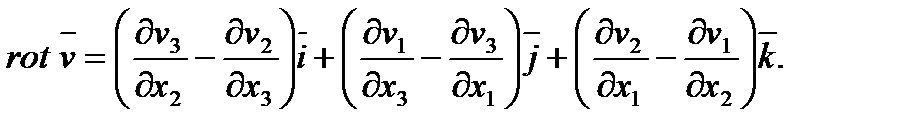
На основании теоремы Стокса имеет место равенство

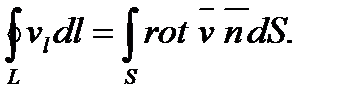
В том случае, когда все проекции скорости 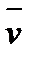могут быть определены одной функцией φ(x_l, x₂, x₃, t) в виде 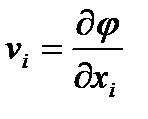, т.е.

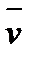= grad φ, то говорят, что поле скоростей потенциальное, функция φ — потенциал скорости. Проекция скорости v₁, на любое направление l определяется производной dφ/dl.

Необходимым и достаточным условием существования потенциальных течений являются равенства

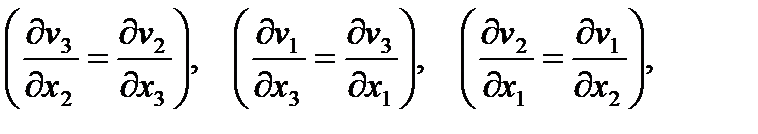иначе, rot 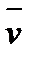= 0. Следовательно, безвихревое течение жидкости потенциально.

§ 2. ЭЛЕМЕНТЫ ТЕОРИИ ДЕФОРМАЦИЙ

Характерной чертой движения сплошной среды является ее

деформация - это изменение расстояния между отдельными точками среды.

Можно доказать, что удлинение (или укорочение) произвольно направленного единичного отрезка 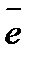, проходящего через какую-либо точку М(х₁, х₂, х₃)среды, вычисляется по формуле

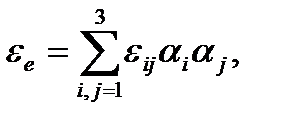(1.16)

где α_ij= 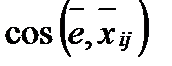— направляющие косинусы отрезка; ε_ii — удлинения (укорочения) единичных отрезков, направленных параллельно координатным осям ox_i; ε_ij = ε_ji(i≠j) — изменения первоначально прямых углов, образованных отрезками, направленными параллельно координатным осям ox_i и ох_j.

Таким образом, деформация элементарного объема среды в окрестности точки М полностью определяется шестью величинами ε_ij, которые называются компонентами тензора деформаций.

Для малых (по сравнению с единицей) деформаций верны следующие соотношения Коши:

в декартовой системе координат

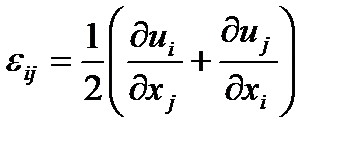(i,j=1, 2, 3), (1.17)

где u_i _, u_j — компоненты вектора перемещения в точке М.

В цилиндрической системе координат (r, Θ, z) при осевой симметрии

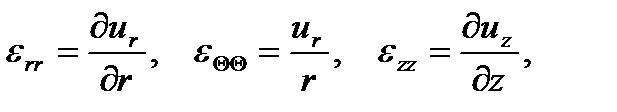
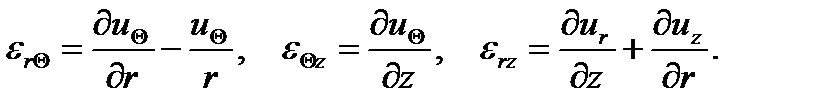(1.18)

Компоненты вектора перемещений u_r, u_Θ, u_z связаны с компонентами

u_i (i=1, 2, 3) обычными соотношениями преобразования координат при повороте системы вокруг оси oz:

u_r= u₁cos Θ + u₂sin Θ,

u_Θ= - u₁ sin Θ + u₂cos Θ,

u_z= u₃.

Если иметь в виду связь между координатами x₁= r cos Θ, x₂ = r sin Θ и x₃ = z, то доказать справедливость перехода от формул (1.17) к формулам (1.18), или наоборот, не представляет труда.

Так как деформация отрезка не зависит от выбора направлений координатных осей, то правая часть в формуле (1.16) инвариантна преобразованию системы координат, т. е.

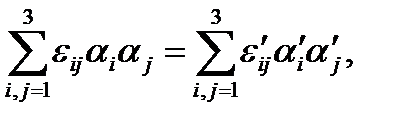(1.19)

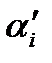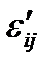где и — направляющие косинусы и компоненты деформаций в новой 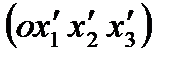системе координат. Для вычисления 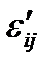через ε_ij, достаточно в равенстве (1.19) выразить 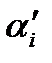через α_i и сравнить коэффициенты при одинаковых α_i, α_j.

В любой точке тела всегда существует по крайней мере одна тройка взаимно перпендикулярных направлений, таких, что деформация элемента в окрестности точки определяется только удлинением (укорочением) ε_ii = ε_i вдоль этих направлений без изменения прямых углов (ε_ij = 0, i≠j). Такие направления называются главными осями деформаций, а величины ε_i (i = 1, 2, 3) — главными удлинениями, которые могут быть найдены из следующего кубического уравнения:

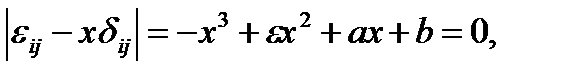
где 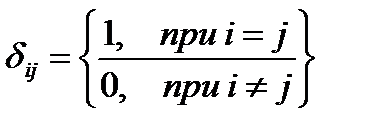— символ Кронекера.

Ясно, что коэффициенты этого уравнения не зависят от выбора системы координат, т. е. они инвариантны. Первый коэффициент ε этого уравнения

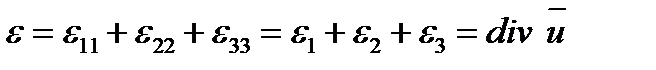(1.20)

и имеет простой геометрический смысл — относительное изменение объема в окрестности точки. Коэффициенты а и b геометрического смысла не имеют и поэтому не являются характеристикой деформаций.

Характеристикой искажения формы элемента сплошной среды служит инвариантная величина

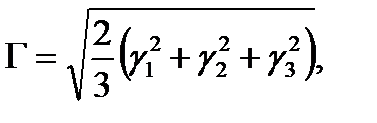
называемая интенсивностью деформаций сдвига.

НБ-09=7.02

Величины γ₁= ε₂- ε₃, γ₂= ε₃– ε₁, γ₃= ε₁– ε₂называются главными сдвигами.

Известно приближенное соотношение

Г=1,08γ_m_ах,

где γ_m_ах — наибольший из главных сдвигов.

В произвольной декартовой системе координат величина Г вычисляется по формуле

Г 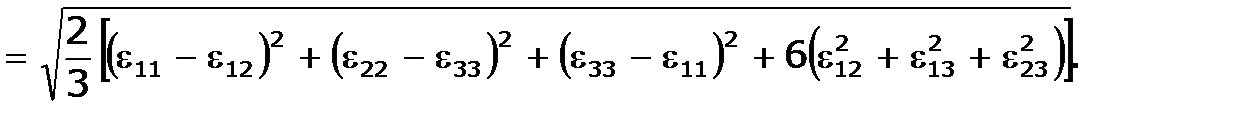(1.21)

Иногда пользуются величиной ε_u = 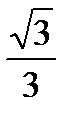Г, называемой приведеннойдеформациейили интенсивностью деформаций.

Для характеристики деформационного состояния служит параметр Надаи

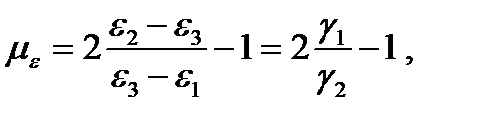(1.22)

который изменяется в пределах от -1 (при чистом удлинении) до +1 (при частичном укорочении). В случае чистого сдвига μ_ε = 0. При всестороннем расширении (или сжатии) μ_εсмысла не имеет.

Часто удобно пользоваться следующим представлением компонент деформаций:

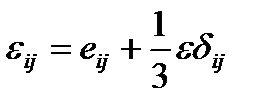, (1.23)

где e_ij — компоненты, характеризующие только деформации сдвига, называемые компонентами девиатора деформаций, δ_ij—символ Кронекера. Отсюда следует, что компоненты тензора деформации растяжения (сжатия) ε_ii отличаются от соответствующих компонент девиатора е_ii на 1/3 объемной деформации, а компоненты деформации сдвига не отличаются, т. е.

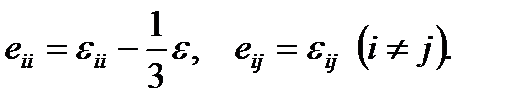
Если известны компоненты деформации ε_ij как функции декартовых координат х_i, то для однозначного определения 3-х компонент u_i вектора перемещений из 6-ти соотношений (1.17) необходимо и достаточно, чтобы функции ε_ij удовлетворяли условиям совместимости (или неразрывности) деформаций Сен-Венана:

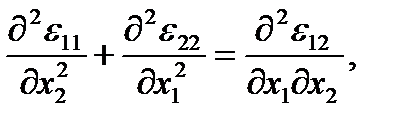
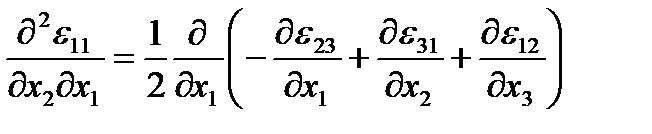(1.24)

и т. д., всего 6 условий (остальные получаются из выписанных круговой заменой индексов 1→2→3→1).

Таким образом, условия совместимости (1.24) являются уравнениями, которые связывают компоненты ε_ij тензора деформаций.

Для анализа больших деформаций, если главные оси при деформации не поворачиваются, используются так называемые натуральные удлинения (укорочения)

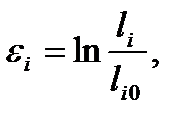
где l_i₀, l_i —начальные и текущие длины элемента в соответствующих направлениях.

Характерные соотношения для малых деформаций являются справедливыми и для натуральных удлинений.

Если скорость частиц сплошной среды 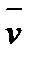= (v ₁, v₂, v₃), то за бесконечно малый промежуток времени dt среда испытывает бесконечно малую деформацию, определяемую перемещениями u_i = v_idt(i = 1, 2, 3). Компоненты этих деформаций, вычисленные по формулам (1.17), имеют общий множитель dt, разделив на который, получим

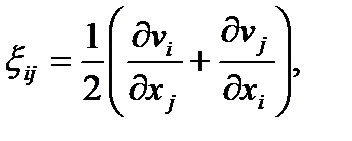(1.25)

где ξ_ij —компоненты тензора скоростей деформаций. Величины ξ_ii определяют скорости удлинения (укорочения) единичных отрезков в направлениях ох_i, ξ_ij(i≠j)— угловые скорости изменения первоначально прямых углов, составленных единичными отрезками вдоль координатных осей.

Подобно формуле (1.16) скорость удлинения (укорочения) любого единичного отрезка вычисляется по формуле

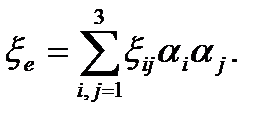
Аналогично соотношениям (1.20) — (1.22) инвариантами скорости деформации являются:

а) скорость относительного объемного расширения (сжатия)

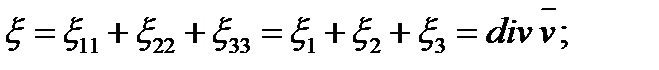(1.26)

б) интенсивность скоростей деформации сдвига относительно главных осей

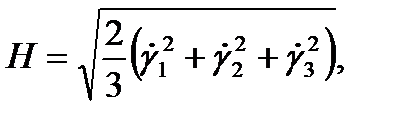(1.27)

где 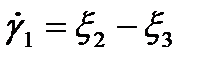, , 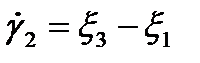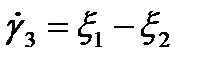— главные скорости сдвигов (относительно произвольной системы координат Н выражается формулой (1.21));

в) параметр Надаи .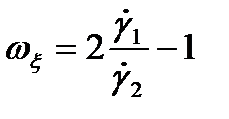

Компоненты скорости деформации ξ_ij, как и компоненты деформации ε_ij, не могут быть произвольными. Они должны удовлетворять условиям совместимости, аналогичным условиям (1.24).

Подобно представлению (1.23) для компонент тензора {ξ_ij} скоростей деформаций верно соотношение

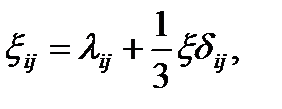(1.28)

где λ_ij — компоненты, характеризующие только скорости деформации сдвига, называемые компонентами девиатора скорости деформаций.

ЭДГб-12-1 4-09-2014

Греческий алфавит

Α α – альфа Ν ν – ни (ню)

Β β – бэта Ξ ξ – кси

Γ γ – гамма Ο ο – омикрон

Δ δ – дельта Π π – пи

Ε ε – эпсилон Ρ ρ – ро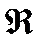

Ζ ζ – дзэза Σ σ – сигма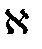

Η η – эта Τ τ – тау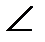

Θ θ – тэта Υ υ – ипсилон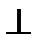

Ι ι – иота Φ φ – фи

Κ κ – каппа Χ χ – хи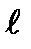

Λ λ – ламбда Ψ ψ – пси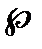

Μ μ – ми (мю) Ω ω – омега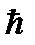

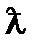
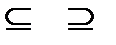
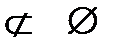
- набла (от греч.-ναβλα - арфа) – знак действия над полем (оператор) –

этот оператор Гамильтона векторно-дифференциальный

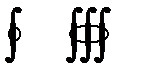
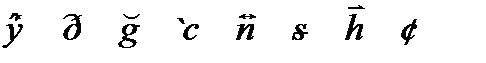
¢ £ ¤ ¥ ¿ ñ æ ě ę Ģ į Ķ Ł ł Œ œ ə ΐ ‰ ₤ ₧ ₪ ₫ € ℅ ™

ТЕНЗОРЫ

Понятие тензора (от латинского tendo — напрягаю, растягиваю) принадлежит к числу основных, фундаментальных математических понятий и широко применяется сейчас в механике, электродинамике, теории относительности и т. д. Первоначально возникшее в работах XIX века по теории упругости, оно было систематически исследовано в 1886 —1901 гг. итальянским геометром Г. Рйччи-Курбастро (1853—1925) и итальянским математиком и механиком Т. Лёви-Чивйта (1873—1942). Внимание к новому аппарату существенно возросло после создания в 1915 —1916 гг. великим ученым, физиком А. Эйнштейном (1879 — 1955) общей теории относительности, математическая часть которой целиком основана на тензорном исчислении. Физические величины, которые нам встречались до сих пор, были либо скалярными, либо векторными. Однако существуют физические величины более сложной природы.

(Q)

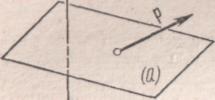Например, однородное напряженное состояние упругого тела характеризуется плотностью р силы, с которой одна часть тела действует на другую через мысленно выделенную плоскость (Q) (рис. 1); однако при этом р для различных направлений плоскости (Q) будет различным. Таким образом, величина, характеризующая напряженное состояние, уже не является вектором, она представляет собой тензор 2-го ранга (определение см. в п. 2). Оказывается, что и многие другие важные величины, характеризующие состояние сплошных сред, также являются тензорами. Рис. 1.

К настоящему времени тензорная алгебра, а также тензорный анализ (т. е. теория тензорных полей, связанная с применением дифференцирования и интегрирования) представляют собой значительно разработанные дисциплины. В этой главе мы осветим лишь самые простые вопросы. Специально тензорному исчислению посвящен ряд книг, из которых мы укажем на [15, 53, 79, 99, 110]; главы, содержащие основы тензорного исчисления, имеются также в [39, 98, 103] и в других книгах.

§ 1. Тензорная алгебра

1. Примеры.К понятию тензора можно прийти уже размышляя над описанием векторов в обычном пространстве с помощью чисел. Как известно из векторной алгебры, все действия над векторами удобно осуществлять, выбрав евклидов базис i, j, k, после чего можно любой вектор а разложить по этому базису

а = а_хi + а_уj+ a_zk (1)

и взамен действий над векторами осуществлять действия над их проекциями, т. е. над числами — коэффициентами разложений. Более того, даже задавать конкретные векторы обычно бывает удобнее с помощью разложения (1), чем каким-то геометрическим способом.

Однако задумаемся теперь, что это за векторы i, j, k. В некоторых случаях, когда в задаче имеется естественная система отсчета направлений (например, во многих задачах статики), эти векторы можно описать вполне точно, «привязав» их к данным задачи. Но во многих случаях привлечение такой «абсолютной» системы отсчета является весьма искусственным либо вообще невозможно. Тогда получается на первый взгляд парадокс: мы пользуемся проекциями вполне определенного вектора, которые зависят от выбора базиса, но не уточняем, как этот базис выбирается...

Эта трудность будет преодолена, если с самого начала отказаться от выбора какого-то одного базиса, а считать, что все базисы равноправны и каждому выбору базиса i, j, k отвечает набор значений а_х, а_у, а_z в соответствии с формулой (1). Подобный набор величин, приобретающих определенные значения лишь после выбора базиса и преобразующихся по определенному правилу при замене базиса (см. ниже), и называется тензором (или тензорной величиной), а сами эти величины, составляющие в определенном порядке тензор, называются его компонентами. (Отметим некоторое несоответствие: в векторной алгебре принято компонентами вектора A называть в е к торы а_х\, а_у\, a_zk. Однако в этой главе мы будем компонентами называть величины а_х, а , а_г.)

Оказывается, удобнее писать е_х, е₃, е₃ И a_lt a_a, а₃ вместо

i, j, k и а_х, а а_г, так что

а = а»е, + а„е₂ + а₃е₃ = 2 afit-

В тензорном исчислении принято не писать знак суммы по повторяющемуся индексу, а при повторении индекса всегда осуществлять такое суммирование, т. е. писать последнюю формулу в виде

а = ap_t ( - я,е,. = a_ke_h = ...). (2)

Здесь индекс суммирования является немым и может быть обозначен любой буквой, а пределы суммирования определяются размерностью пространства, в котором рассматривается тензор.

Лекция 2. § 3. ДИНАМИЧЕСКИЕ ВЕЛИЧИНЫ

<12 3 4 5 6 7 >

Дата добавления: 2015-12-11; просмотров: 797;