ФОРМУЛА ДЮПЮИ И ЕЕ ОБОБЩЕНИЯ
Одна из основных практически важных стационарных задач фильтрации – определение расхода жидкости при поглощении или проявлении пласта, искусственном нагнетании жидкости в пласт или отборе ее из пласта, а также определение параметров пласта и призабойной зоны при гидродинамических испытаниях скважин.
1. Простейшее решение этой задачи базируется на следующих предпосылках:
а) однородный изотропный пористый, трещиноватый или трещиновато-пористый пласт проницаемостью 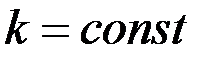 ограничен непроницаемыми плоскостями
ограничен непроницаемыми плоскостями 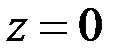 и
и 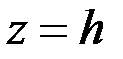 (кровля и подошва пласта) и проницаемыми цилиндрическими поверхностями
(кровля и подошва пласта) и проницаемыми цилиндрическими поверхностями 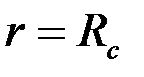 (стенка скважины),
(стенка скважины), 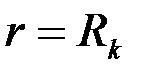 (поверхность питания), на которых поддерживаются однородные граничные условия
(поверхность питания), на которых поддерживаются однородные граничные условия
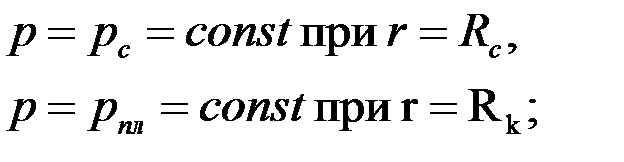
| (3.55) |
б) поры пласта заполнены однородной невесомой жидкостью вязкости 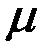 ;
;
в) фильтрация происходит при жестком 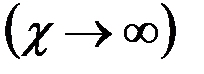 или установившемся
или установившемся 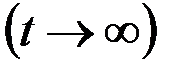 ламинарном режиме.
ламинарном режиме.
Основные уравнения теории фильтрации в этом случае запишутся в виде
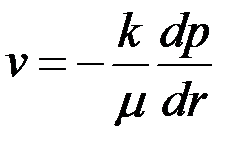
| (3.56) |
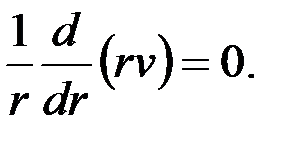
| (3.57) |
Подстановка (3.56) в (3.57) дает простейший вид уравнения Лапласа
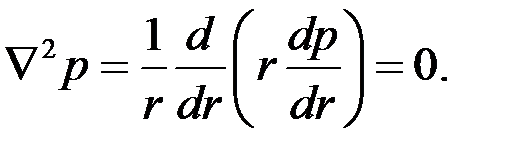
|
Общим решением этого уравнения является функция
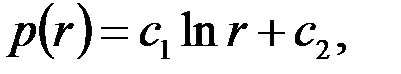
| (3.58) |
где 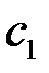 и
и 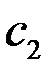 – постоянные интегрирования, определяемые граничными условиями (3.55).
– постоянные интегрирования, определяемые граничными условиями (3.55).
В результате получим решение первой основной граничной задачи фильтрации (3.55 – 3.57):
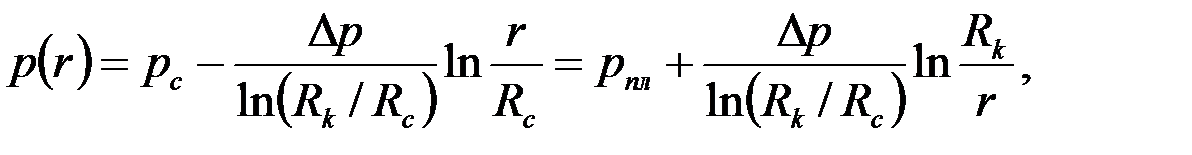
| (3.59) |
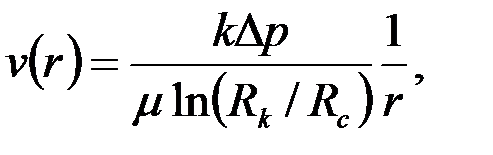
| (3.60) |
где 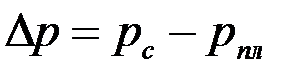 – заданный перепад давления между скважиной и пластом.
– заданный перепад давления между скважиной и пластом.
При поглощении 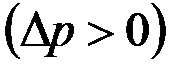 проявлении
проявлении 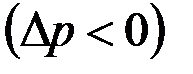 пласта объемный расход жидкости через любую цилиндрическую поверхность
пласта объемный расход жидкости через любую цилиндрическую поверхность 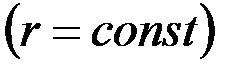 , в том числе и через стенку скважины,
, в том числе и через стенку скважины,
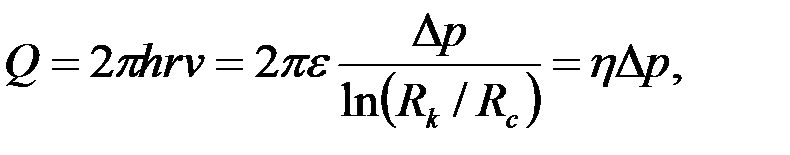
| (3.61) |
где 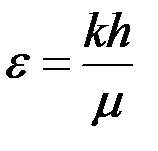 ;
; 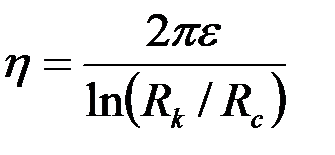 – соответственно коэффициент гидропроводности, или просто гидропроводность, и коэффициент продуктивности, или просто продуктивность пласта; размерность м3/Па.с.
– соответственно коэффициент гидропроводности, или просто гидропроводность, и коэффициент продуктивности, или просто продуктивность пласта; размерность м3/Па.с.
Формула (3.61) впервые получена французским инженером Дюпюи и поэтому названа его именем.
2. Используя формулу (3.61) в решении (3.59), непосредственно решается вторая основная граничная задача [см. условие (2.37)], когда у стенки скважины 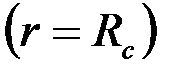 заданы скорость фильтрации и расход жидкости
заданы скорость фильтрации и расход жидкости 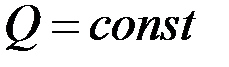 . Распределение давления в этом случае описывается формулой
. Распределение давления в этом случае описывается формулой
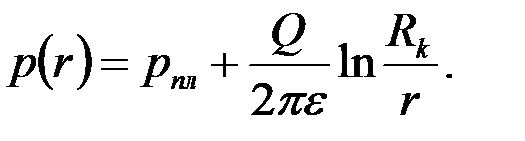
| (3.62) |
Важно подчеркнуть, что это решение совпадает с фундаментальным решением двумерного уравнения Лапласа (2.34), когда в плоскости действуют источник 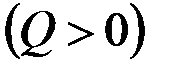 или сток
или сток 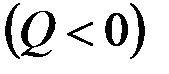 интенсивности
интенсивности 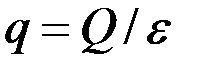 .
.
Следовательно, влияние работы скважины на изменение давления в пласте аналогично работе источника (или стока). Этот результат часто используется как простой метод решения сложных задач фильтрации в прискважинной области. Далее мы неоднократно будем пользоваться этим методом.
3. В реальной ситуации благодаря наличию глинистой корки, зон кольматации, загрязнения, искусственной трещиноватости (при гидроразрыве) и т. д. проницаемость произвольной зоны скважины может сильно отличаться от проницаемости остальной части пласта. Учесть влияние этой неоднородности можно двумя способами.
Первый способ заключается в замене граничного условия 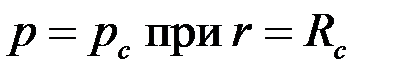 условием вида (2.38)
условием вида (2.38)
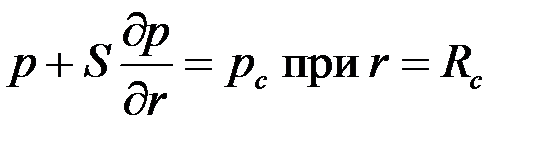 , ,
| (3.63) |
где 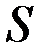 - безразмерный параметр, характеризующий степень роста поверхностного сопротивления при
- безразмерный параметр, характеризующий степень роста поверхностного сопротивления при 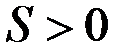 (глинистая корка, кольматации, загрязнение и т. д.) или его снижение при
(глинистая корка, кольматации, загрязнение и т. д.) или его снижение при 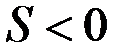 (декольматации, поверхностные трещины, установлен фильтр высокой проницаемости); при
(декольматации, поверхностные трещины, установлен фильтр высокой проницаемости); при 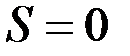 граничное условие (3.63) совпадает с первым условием (3.39).
граничное условие (3.63) совпадает с первым условием (3.39).
Используя общее решение (3.58), граничное условие (3.63) и условие 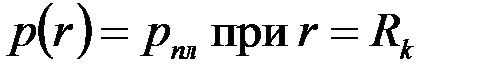 без труда найдем, что решение этой задачи также имеет вид (3.58) – (3.61), необходимо только заменить истинный радиус скважины
без труда найдем, что решение этой задачи также имеет вид (3.58) – (3.61), необходимо только заменить истинный радиус скважины 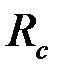 приведенным:
приведенным:
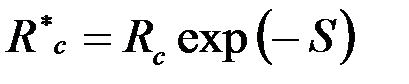 . .
| (3.64) |
В частности, формула Дюпюи (3.61) принимает следующий обобщенный вид:
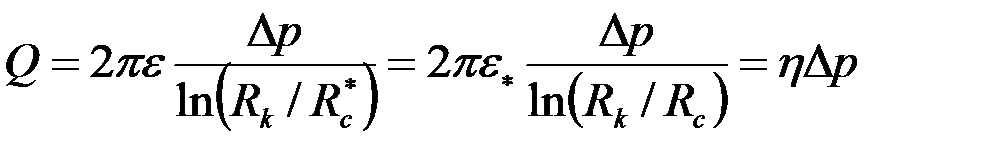 , ,
| (3.65) |
где 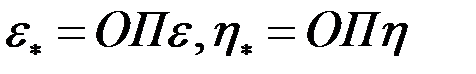 - приведенные коэффициенты гидропроводности и продуктивности пласта;
- приведенные коэффициенты гидропроводности и продуктивности пласта;
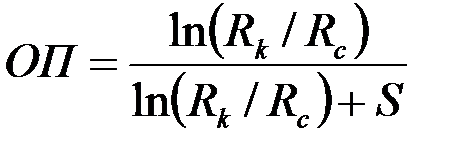 . .
| (3.66) |
Как будет показано ниже, к формуле (3.65) сводятся решения разных граничных задач фильтрации.
Параметр ОП дает количественную оценку снижения (при S>0) или увеличения (при S<0) гидропроводности и продуктивности пласта вследствие кольматации или декольматации приствольной части пласта. Поэтому он используется в настоящее время как
основной показатель
качества вскрытия продуктивных пластов, освоения и заканчивания скважин.
Для определения показателя ОП необходимо, как следует из формул (3.49) и (3.50), найти параметры 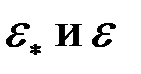 или параметр S при известном отношении
или параметр S при известном отношении 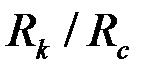 .
.
Приведенная (или фактическая) гидропроводность пласта 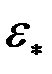 устанавливается по индикаторной диаграмме (ИД) – зависимости
устанавливается по индикаторной диаграмме (ИД) – зависимости 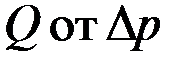 , получаемой при исследовании скважины методом установившихся отборов. Истинная (или потенциальная) гидропроводность пласта
, получаемой при исследовании скважины методом установившихся отборов. Истинная (или потенциальная) гидропроводность пласта 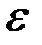 определяется обычно по кривой восстановления давления (КВД) – зависимости
определяется обычно по кривой восстановления давления (КВД) – зависимости 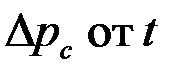 , получаемой при исследовании скважины на неустановившемся режиме фильтрации. По КВД при дополнительных сведениях о пласте находят параметр S.
, получаемой при исследовании скважины на неустановившемся режиме фильтрации. По КВД при дополнительных сведениях о пласте находят параметр S.
Второй способ решения данной задачи заключается в рассмотрении плоско-радиальной фильтрации для составной области, состоящей из приствольной зоны 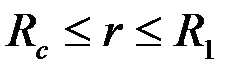 , постоянной или переменной по
, постоянной или переменной по 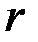 проницаемостью
проницаемостью 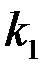 , и удаленной части пласта
, и удаленной части пласта 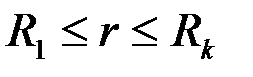 с проницаемостью
с проницаемостью 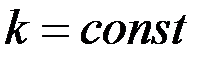 .
.
Если принять 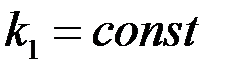 , то для каждой из однородных областей имеем решение вида (3.42)
, то для каждой из однородных областей имеем решение вида (3.42)
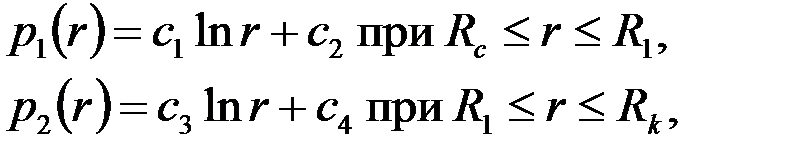
| (3.67) |
где константы 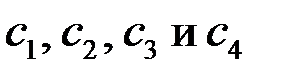 определяются из 4-х граничных условий
определяются из 4-х граничных условий
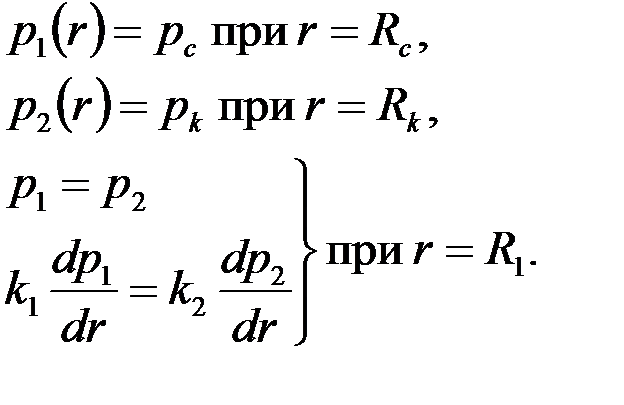
| (3.68) |
В результате простых вычислений получим следующее решение задачи [сравн. с формулой (3.62)]:
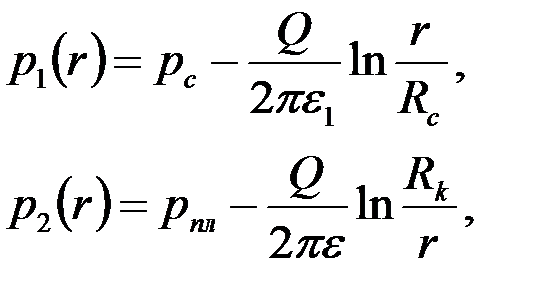
| (3.69) |
где 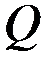 - расход, определяемый по формуле
- расход, определяемый по формуле
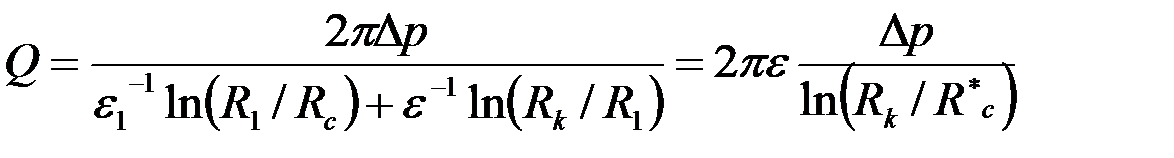 ; ;
|
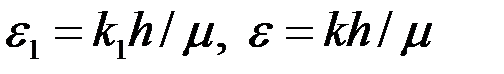 - гидропроводности приствольной и удаленной частей пласта;
- гидропроводности приствольной и удаленной частей пласта; 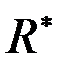 - приведенный радиус скважины:
- приведенный радиус скважины:
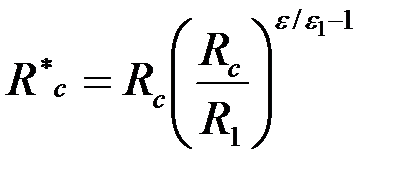 . .
| (3.70) |
Сравнивая правые части (3.64) и (3.70), получим известную формулу для вычисления показателя «скин-эффекта»
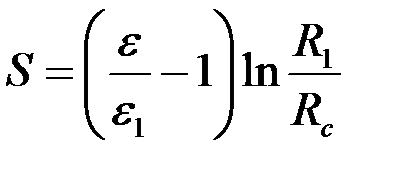 . .
| (3.71) |
Отсюда и из формулы (3.66) следует:
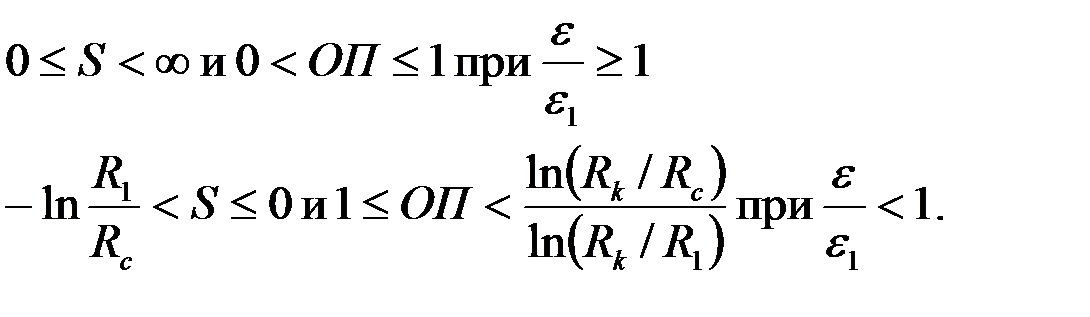
|
Так как 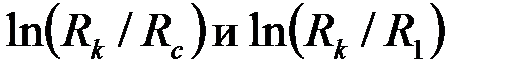 очень близкие величины, то понятно, что увеличение проницаемости приствольной зоны оказывает слабое влияние на гидропроводность пласта. В то же время уменьшение проницаемости приствольной зоны может оказать существенное влияние на снижение гидропроводности пласта. Например, при
очень близкие величины, то понятно, что увеличение проницаемости приствольной зоны оказывает слабое влияние на гидропроводность пласта. В то же время уменьшение проницаемости приствольной зоны может оказать существенное влияние на снижение гидропроводности пласта. Например, при 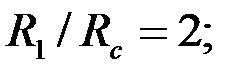
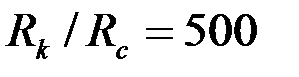 и
и 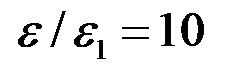 получим
получим 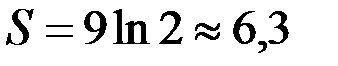 и
и 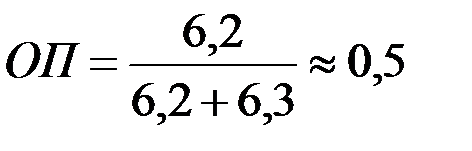 , т. е. гидропроводность пласта уменьшится в 2 раза. Но при
, т. е. гидропроводность пласта уменьшится в 2 раза. Но при 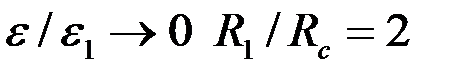 , что соответствует увеличению диаметра скважины в 2 раза, имеем
, что соответствует увеличению диаметра скважины в 2 раза, имеем 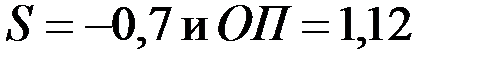 , т. е. гидропроводность пласта увеличится всего на 12%.
, т. е. гидропроводность пласта увеличится всего на 12%.
4. В том случае, когда приствольная зона скважины 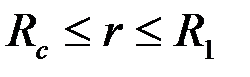 представляет собой область непрерывного изменения проницаемости
представляет собой область непрерывного изменения проницаемости 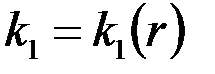 , уравнение неразрывности (3.57) видоизменится:
, уравнение неразрывности (3.57) видоизменится:
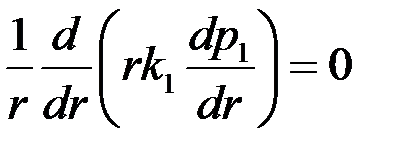 . .
| (3.72) |
Для удаленной части пласта 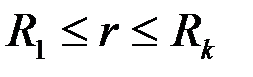 распределение давления
распределение давления 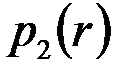 соответствует решению (3.51), а для приствольной зоны путем интегрирования (3.56) находим
соответствует решению (3.51), а для приствольной зоны путем интегрирования (3.56) находим
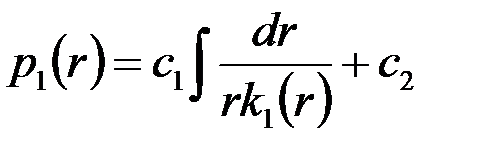 . .
| (3.73) |
Примем закономерность изменения проницаемости в области 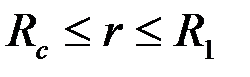 в виде
в виде
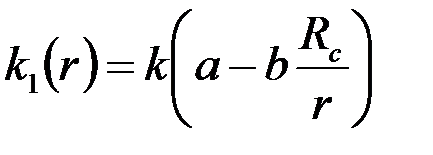 , ,
|
где 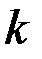 – проницаемость удаленной части пласта, т. е. при
– проницаемость удаленной части пласта, т. е. при 
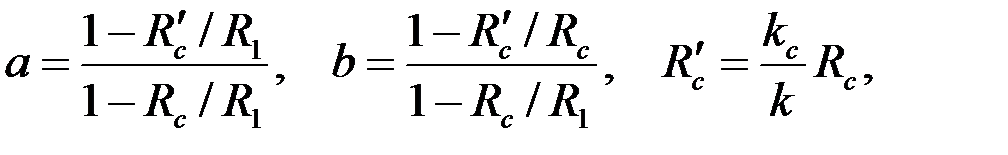
|
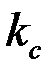 – проницаемость стенки скважины
– проницаемость стенки скважины 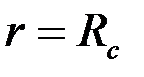 .
.
После подстановки 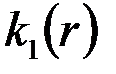 в (3.73),интегрирования и определения постоянных
в (3.73),интегрирования и определения постоянных 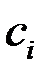 из граничных условий (3.68) получим следующее решение задачи:
из граничных условий (3.68) получим следующее решение задачи:
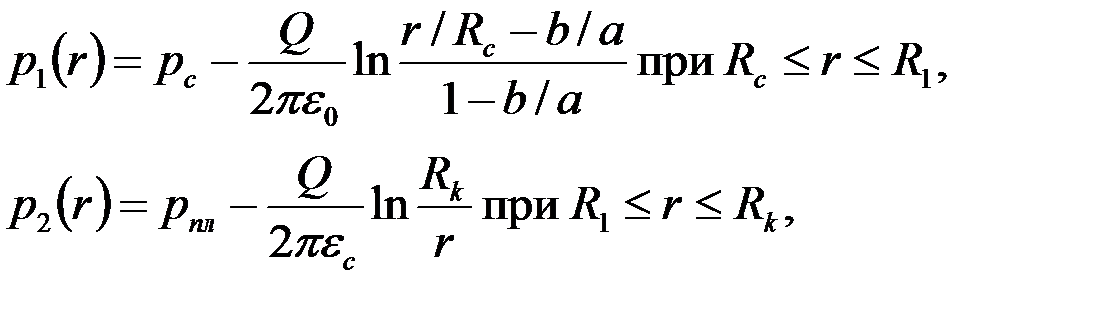
|
где 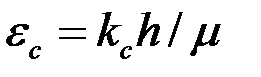 , а расход
, а расход  вычисляется по обобщенной формуле Дюпюи (3.65), в которой приведенный радиус скважины надо принять
вычисляется по обобщенной формуле Дюпюи (3.65), в которой приведенный радиус скважины надо принять
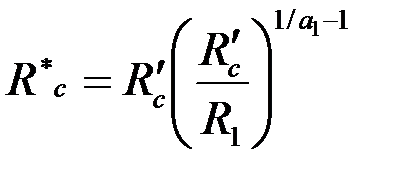 . .
|
Используя сходство этой формулы с формулой (3.70), легко найти
параметр 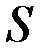 , исходя непосредственно из формулы (3.71):
, исходя непосредственно из формулы (3.71):
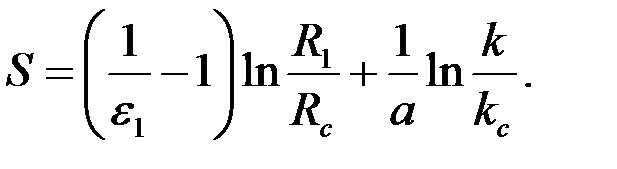
|
Пусть, например, при бурении проницаемого интервала 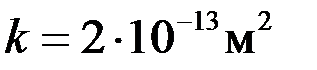
на стенке скважины сформирована глинистая корка проницаемостью 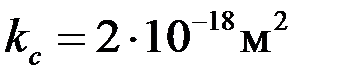 , т. е.
, т. е. 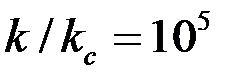 и
и 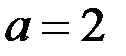 . Принимая
. Принимая 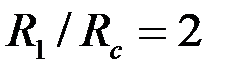 и
и 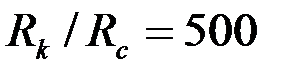 , получим
, получим
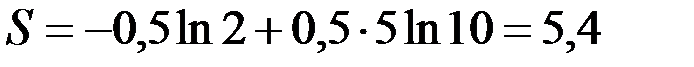 и
и 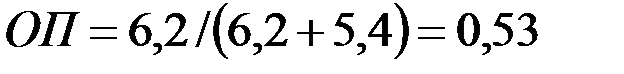 ,
,
т. е. поглощение фильтрата бурового раствора уменьшится более чем в 2 раза.
5.Если пласт содержит упорядоченную систему трещин, то в нем благодаря анизотропии проницаемости плоско-радиальный характер фильтрации не будет иметь место (см. разд. 2).
Рассмотрим случай, когда одно из главных направлений анизотропии Ox3 совпадает с направлением оси скважины Oz (например, упорядоченная система вертикальных трещин в вертикальной скважине). Тогда два других главных направления анизотропии Ох1 и Ох2 расположены в плоскости 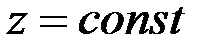 , т. е. параллельно кровле и подошве пласта. При заданных однородных граничных условиях в скважине и на поверхности питания (3.55) фильтрация будет плоской, так как
, т. е. параллельно кровле и подошве пласта. При заданных однородных граничных условиях в скважине и на поверхности питания (3.55) фильтрация будет плоской, так как 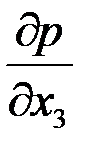 , но не радиальной. В плоскости х1х2 имеют место обобщенный закон Дарси [см. формулу (2.40)]
, но не радиальной. В плоскости х1х2 имеют место обобщенный закон Дарси [см. формулу (2.40)]
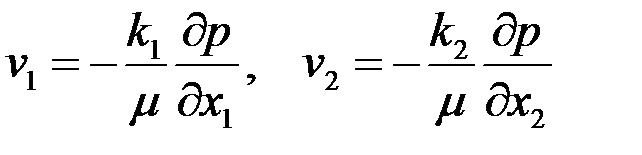 , ,
|
и соответствующее ему уравнение неразрывности [см. формулу (2.42)]
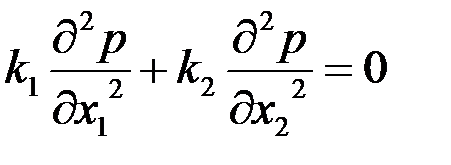 . .
| (3.74) |
Как было сказано в разд. 2, введением новой системы координат
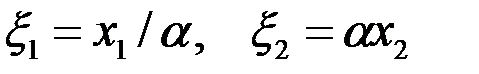
| (3.75) |
уравнение (3.74),заданное в анизотропной плоскости х1х2, преобразуется в уравнение Лапласа
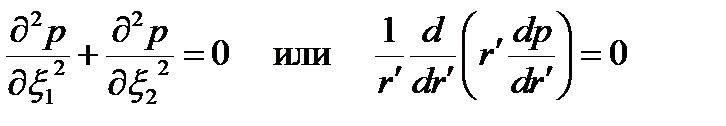 . .
| (3.76) |
для изотропной плоскости 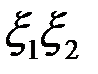 , проницаемость которой
, проницаемость которой
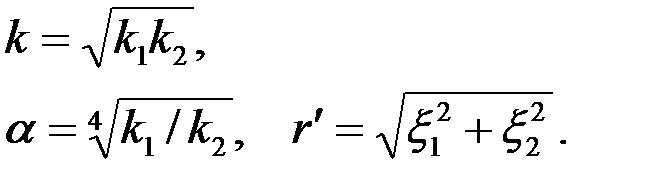
|
Принимая скважину в качестве источника (или стока) интенсивностью 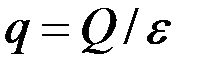 , получим, аналогично (3.62), поле давления
, получим, аналогично (3.62), поле давления
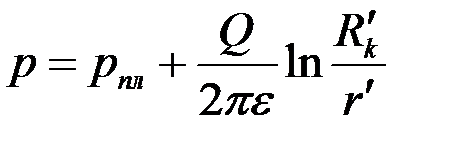 . .
| (3.77) |
где 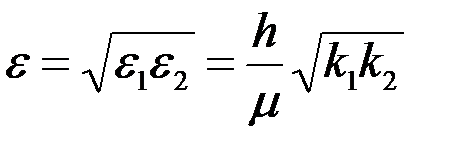 ,
, 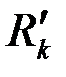 – радиус контура питания в плоскости
– радиус контура питания в плоскости 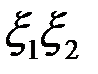 . Отсюда следует, что эквипотенциальной поверхностью
. Отсюда следует, что эквипотенциальной поверхностью 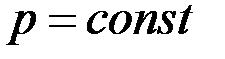 являются: окружность
являются: окружность 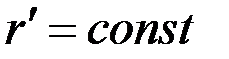 в плоскости
в плоскости 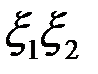 и эллипс
и эллипс 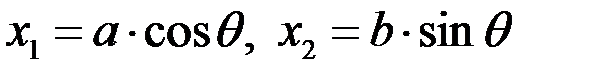 в плоскости х1х2, где
в плоскости х1х2, где 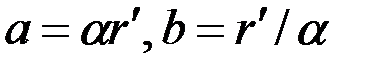 – полуоси эллипса.
– полуоси эллипса.
Это означает, что контуром питания (где 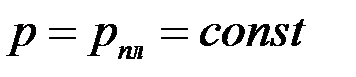 ) в анизотропном пласте может быть только эллипс
) в анизотропном пласте может быть только эллипс
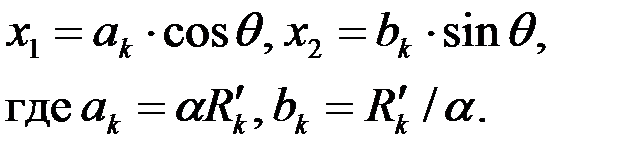
| (3.78) |
Согласно (3.59) этому эллипсу в плоскости 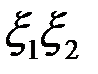 соответствует окружность
соответствует окружность 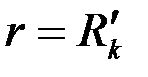 . В то же время окружность
. В то же время окружность 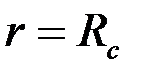 преобразуется в эллипс
преобразуется в эллипс
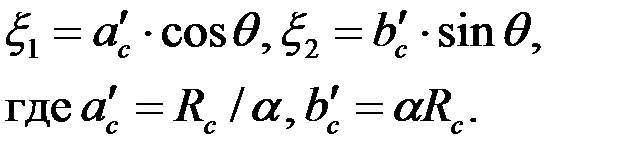
| (3.79) |
Поэтому в строгой постановке первая основная граничная задача формулируется так: найти решение уравнения (3.76), удовлетворяющее условию 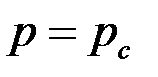 в точках эллипса (3.79) и условию
в точках эллипса (3.79) и условию 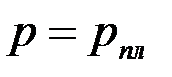 на окружности
на окружности 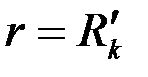 .
.
Однако для определения расхода 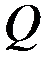 ‚ достаточно хорошее приближение получается, если эллипс (3.79) заменить эквивалентной окружностью радиуса
‚ достаточно хорошее приближение получается, если эллипс (3.79) заменить эквивалентной окружностью радиуса
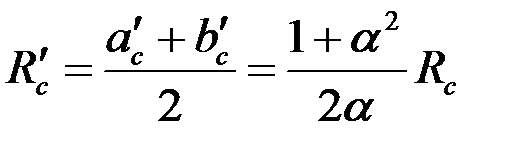 . .
| (3.80) |
Используя в (3.61) условие 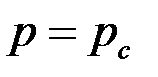 при
при 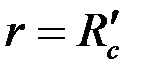 получим
получим
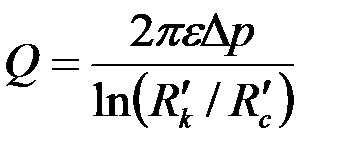 . .
| (3.81) |
Если истинный эллиптический контур питания (3.78) заменить условным – окружностью радиуса
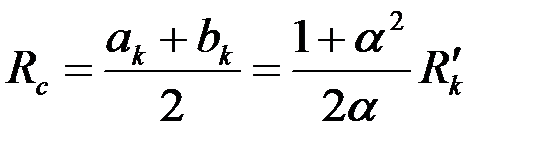
| (3.82) |
то, выразив 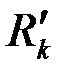 через
через 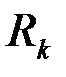 и подставив полученное выражение и соотношение (3.80) в (3.81) придем к обычной формуле Дюпюи (3.65), в которой
и подставив полученное выражение и соотношение (3.80) в (3.81) придем к обычной формуле Дюпюи (3.65), в которой 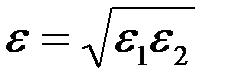 , а приведенный радиус скважины, приведенные коэффициенты гидропроводности и продуктивности надо принять равными:
, а приведенный радиус скважины, приведенные коэффициенты гидропроводности и продуктивности надо принять равными:
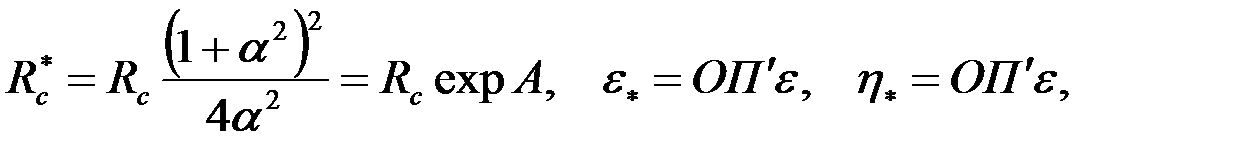
| (3.83) |
где 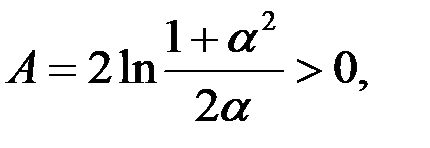
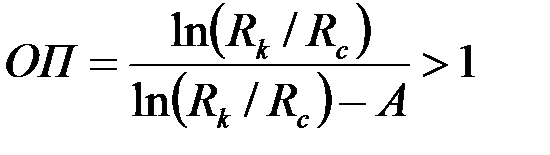 . .
| (3.84) |
Отсюда следует, что при прочих равных условиях в анизотропном пласте расход жидкости выше, чем в изотропном пласте эквивалентной гидропроводности 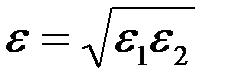 .
.
В нижеследующей таблице приведены значения  при нескольких параметрах анизотропии
при нескольких параметрах анизотропии  и
и  .
.
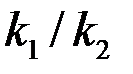
| 102 | 103 | 104 | |||

| 1,03 | 1,05 | 1,15 | 1,21 | 1,50 | 2,05 |
Видно, что влияние анизотропии заметно при больших отношениях 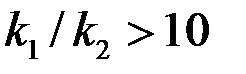 .
.
6. Если после вскрытия пласта проницаемости 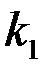 и
и 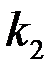 в приствольной зоне скважины изменились и стали равными
в приствольной зоне скважины изменились и стали равными 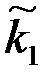 и
и 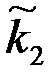 то возникает задача об определении расхода в неоднородном анизотропном пласте. Приближенное решение этой задачи может быть без труда найдено при следующих условиях:
то возникает задача об определении расхода в неоднородном анизотропном пласте. Приближенное решение этой задачи может быть без труда найдено при следующих условиях:
главные направления проницаемостей в приствольной зоне и удаленной части пласта совпадают;
границей раздела областями является эллипс
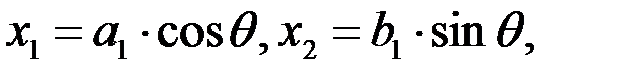
| (3.85) |
где 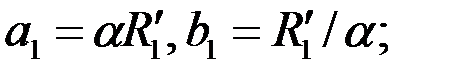
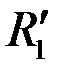 – радиус границы раздела в преобразованной плоскости
– радиус границы раздела в преобразованной плоскости 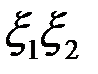 .
.
Обозначим давление на общей границе через 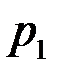 и рассмотрим каждую из областей независимо друг от друга.
и рассмотрим каждую из областей независимо друг от друга.
Так как подобным эллипсам (3.78) и (3.85) в плоскости 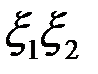 соответствуют концентрические окружности
соответствуют концентрические окружности 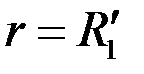 и
и 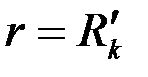 , то для удаленной части пласта имеем [см. формулу (3.81)]
, то для удаленной части пласта имеем [см. формулу (3.81)]
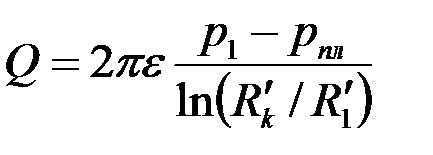 , ,
| (3.86) |
где 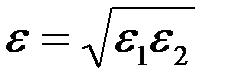 –приведенная гидропроводность удаленной части пласта. Рассматривая приствольную зону скважины, замечаем, что здесь преобразование системы координат х1х2 в
–приведенная гидропроводность удаленной части пласта. Рассматривая приствольную зону скважины, замечаем, что здесь преобразование системы координат х1х2 в 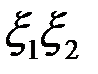 осуществляется с помощью другого параметра анизотропии
осуществляется с помощью другого параметра анизотропии 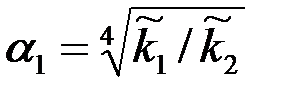 ,т. е.
,т. е.
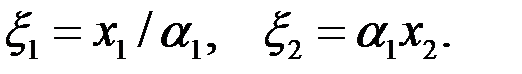
|
Следовательно, границы этой области: эллипс (3.69) и окружность 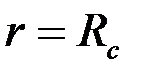 преобразуются в эллипсы с соответствующими полуосями
преобразуются в эллипсы с соответствующими полуосями
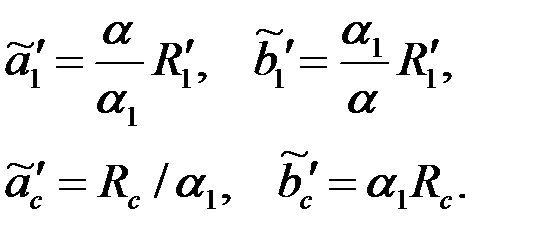
|
Заменив эти эллипсы эквивалентными окружностями, радиусы которых равны
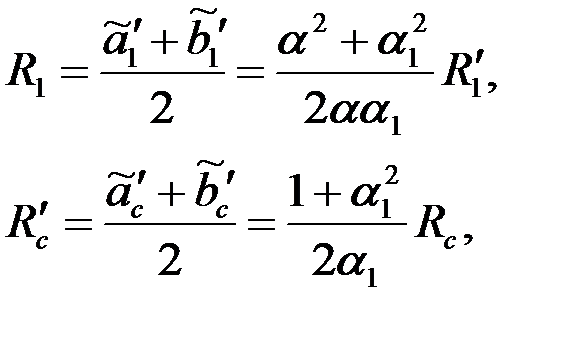
| (3.87) |
получим приближенную формулу для расхода жидкости
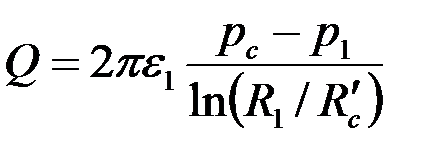 , ,
| (3.88) |
где 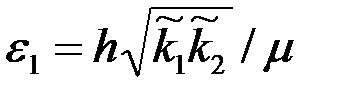 – приведенная гидропроводность призабойной части пласта.
– приведенная гидропроводность призабойной части пласта.
Определив 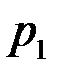 из равенства правых частей (3.86) и (3.88), после преобразования получим следующую обобщенную формулу Дюпюи:
из равенства правых частей (3.86) и (3.88), после преобразования получим следующую обобщенную формулу Дюпюи:
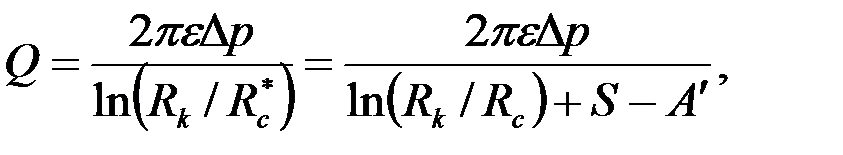 , ,
| (3.89) |
где
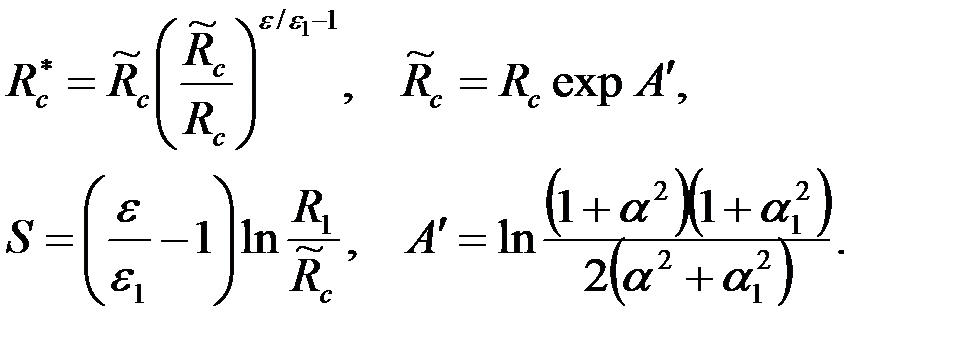 . .
|
Видно, что при 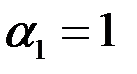 и
и 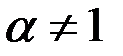 имеем
имеем 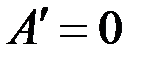 , т. е. влияние анизотропии исчезает, если призабойная зона скважины в результате кольматации приобрела свойства изотропной среды. Аналогичный результат имеет место при
, т. е. влияние анизотропии исчезает, если призабойная зона скважины в результате кольматации приобрела свойства изотропной среды. Аналогичный результат имеет место при 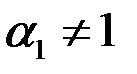 и
и 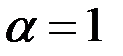 , что возможно, например, при гидроразрыве изотропного пласта. Отсюда следует вывод гидроразрыв гранулярного коллектора в ПЗ не может привести к заметному росту продуктивности скважины. Его положительная роль сводится к разрушению зоны кольматации и тем самым восстановлению потенциальной продуктивности пласта. Только при гидроразрыве анизотропного пласта, когда
, что возможно, например, при гидроразрыве изотропного пласта. Отсюда следует вывод гидроразрыв гранулярного коллектора в ПЗ не может привести к заметному росту продуктивности скважины. Его положительная роль сводится к разрушению зоны кольматации и тем самым восстановлению потенциальной продуктивности пласта. Только при гидроразрыве анизотропного пласта, когда 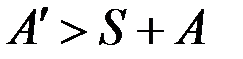 , продуктивность скважины может быть увеличена.
, продуктивность скважины может быть увеличена.
7. Фильтрация, отличная от плоско-радиальной, возникает и в том случае, когда пласт вскрыт не на всю мощность, а частично или часть пласта перекрыта обсадной колонной, или связь пластовой и скважинной жидкостей осуществляется через перфорационные отверстия в колонне.
В этих случаях говорят о несовершенном вскрытии пласта и задают граничное условие 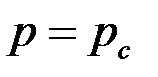 лишь на открытой части поверхности
лишь на открытой части поверхности 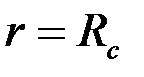 , а на остальной условие непроницаемости
, а на остальной условие непроницаемости 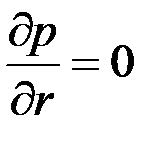 . Течение жидкости в таких условиях вблизи скважины пространственно, и, естественно, решение задачи фильтрации усложняется.
. Течение жидкости в таких условиях вблизи скважины пространственно, и, естественно, решение задачи фильтрации усложняется.
Известны различные приближенные аналитические решения этих задач и экспериментальные исследования на моделях, учитывающие тот или иной вид несовершенства вскрытия пласта.
Общий вывод, который следует из полученных решений, сводится к тому, что расход жидкости и в этих случаях вычисляется по обобщенной формуле Дюпюи (3.49), где приведенный радиус скважины
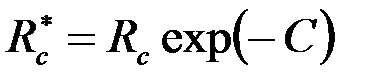 , ,
| (3.90) |
здесь 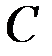 – показатель фильтрационного сопротивления, связанный с несовершенством вскрытия пласта.
– показатель фильтрационного сопротивления, связанный с несовершенством вскрытия пласта.
Отношение расхода жидкости 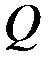 при несовершенном вскрытии к расходу
при несовершенном вскрытии к расходу 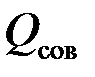 при совершенном вскрытии пласта в тех же условиях определяют аналогично параметру ОП [см. формулу (3.66)]
при совершенном вскрытии пласта в тех же условиях определяют аналогично параметру ОП [см. формулу (3.66)]
коэффициент сопротивления:
| (3.91) |
В общем случае 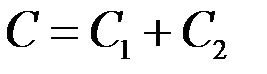 где
где 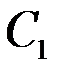 и
и 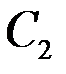 – показатели сопротивления, обусловленные несовершенством по степени и характеру вскрытия пласта. Для случая вскрытия части пласта
– показатели сопротивления, обусловленные несовершенством по степени и характеру вскрытия пласта. Для случая вскрытия части пласта 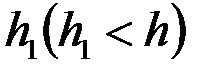 Маскет, используя метод источников, нашел, что при
Маскет, используя метод источников, нашел, что при 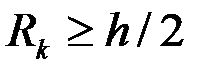 показатель несовершенства по степени вскрытия можно определить по формуле
показатель несовершенства по степени вскрытия можно определить по формуле
|
Здесь 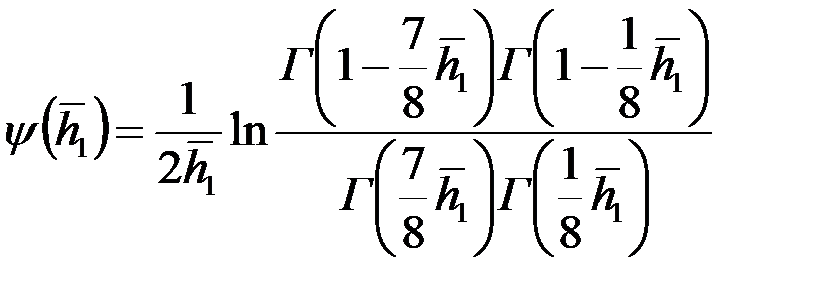 ,
,
где 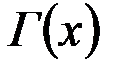 – гамма-функция (известная, табулированная функция);
– гамма-функция (известная, табулированная функция); 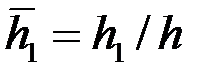 .
.
Представление о функции 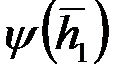 и показателе
и показателе 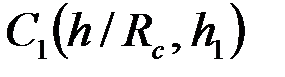 дает табл. 3.
дает табл. 3.
Таблица 3
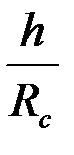
| 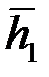
| |||||||
| 0,9 | 0,8 | 0,7 | 0,6 | 0,5 | 0,4 | 0,3 | 0,2 | |
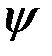
| ||||||||
| 0,43 | 0,84 | 1,38 | 2,04 | 2,93 | 4,33 | 7,1 | 13,11 | |
| 0,16 | 0,47 | 0,91 | 1,52 | 2,35 | 2,62 | 5,35 | 8,1 | |
| 0,24 | 0,65 | 1,21 | 1,98 | 3,04 | 3,65 | 6,87 | 10,87 | |
| 0,41 | 1,05 | 1,89 | 3,05 | 4,66 | 6,07 | 10,63 | 17,39 | |
| 0,49 | 1,22 | 2,19 | 3,52 | 5,35 | 7,11 | 12,24 | 20,08 |
Например, при Rc = 0,1 м, h = 20 м, h1 = 10 м, согласно таблице при h/Rc=200 и h1=0,5, получим С1=З,35, что при 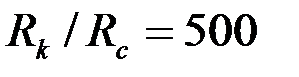 соответствует коэффициенту сопротивления КС = 0,65.
соответствует коэффициенту сопротивления КС = 0,65.
Существенное значение в этой задаче могут иметь различные проницаемости вдоль пласта 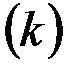 и в направлении, перпендикулярном к пласту
и в направлении, перпендикулярном к пласту 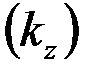 , т. е. анизотропия проницаемости. Доказано, что учесть этот фактор можно, если заменить истинную мощность пласта
, т. е. анизотропия проницаемости. Доказано, что учесть этот фактор можно, если заменить истинную мощность пласта 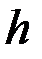 приведенной
приведенной 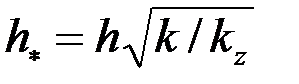 .
.
Если, например, 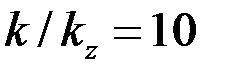 , то по данным предыдущего примера имеем
, то по данным предыдущего примера имеем 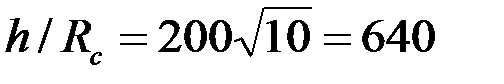 ,
, 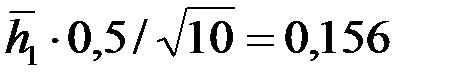 и, согласно формулам,
и, согласно формулам, 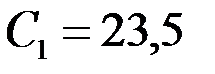 и
и 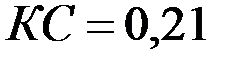 .
.
Несовершенство по характеру вскрытия имеет место, когда связь со скважиной осуществляется через круглые или щелевые отверстия в обсадной колонне. В этом случае показатель несовершенства может быть вычислен по следующим приближенным формулам:
|
где 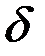 – открытая часть поверхности колонны;
– открытая часть поверхности колонны; 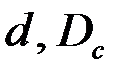 – диаметры перфорационных отверстий и скважины; т — число рядов щелей.
– диаметры перфорационных отверстий и скважины; т — число рядов щелей.
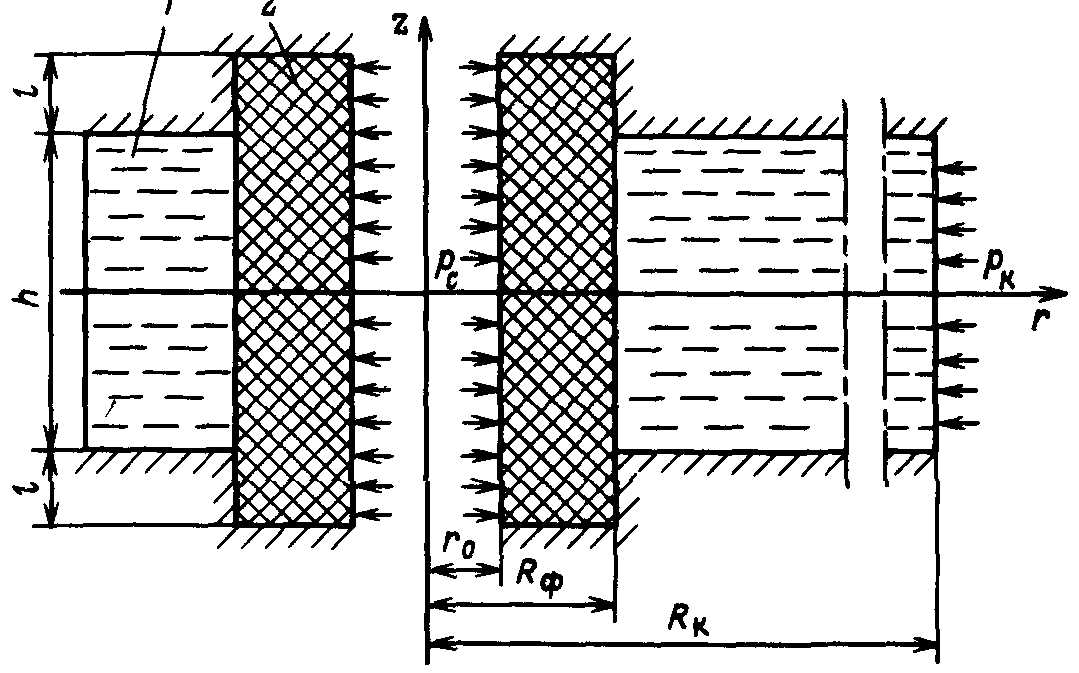
Рис. 3.5 Схема призабойной зоны скважины с искусственным фильтром
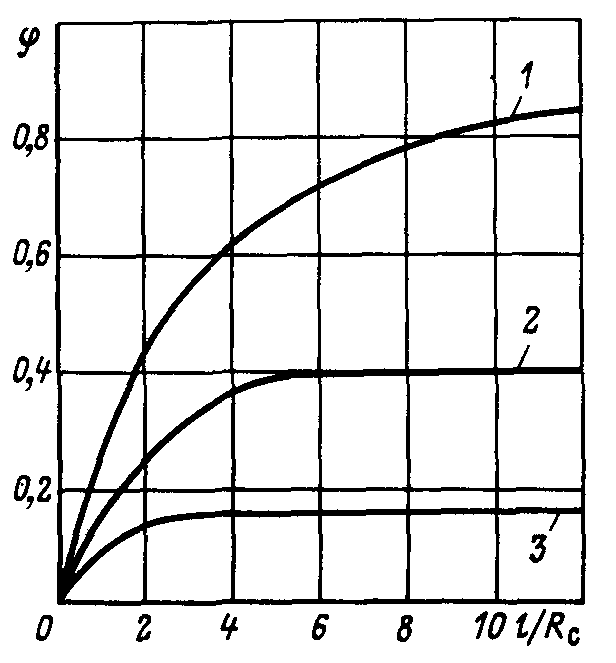
Рис. 3.6 Зависимость показателя снижения фильтрационного сопротивления от величины дополнительной зоны фильтрации при h/Re = 15: 1 2, 3 соответственно при Rф/Rc = 8; 5; 3
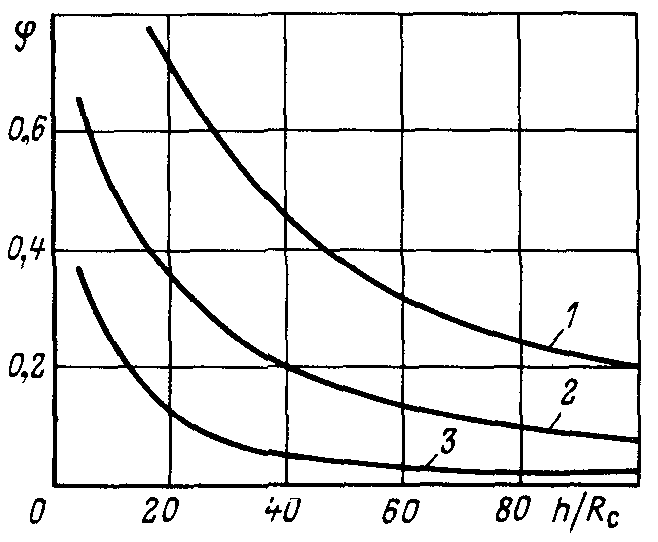
Рис. 3.7Зависимость показателя снижения фильтрационного сопротивления от мощности пласта и радиуса фильтра приl/Rф = 2: 1, 2, 3 соответственно
при Rф/Rc = 8; 5; 3
Приведем решение задачи, когда приствольная зона скважины оборудована искусственным фильтром (2)высотой 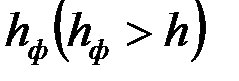 и проницаемостью
и проницаемостью 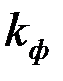 , отличной от проницаемости пласта (1)(рис. 3.5).
, отличной от проницаемости пласта (1)(рис. 3.5).
Приведенный радиус в этом случае
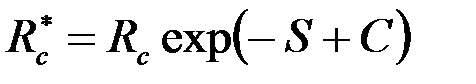 , ,
| (3.92) |
где 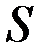 – параметр «скин-эффекта» [см. формулу (3.71)];
– параметр «скин-эффекта» [см. формулу (3.71)]; 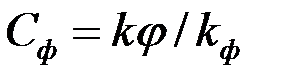 показатель снижения сопротивления, обусловленный наличием дополнительной зоны
показатель снижения сопротивления, обусловленный наличием дополнительной зоны 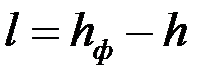 ;
; 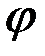 – функция безразмерных параметров
– функция безразмерных параметров 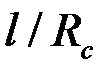 ,
, 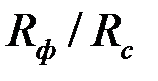 ,
, 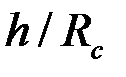 .
.
На рис.3.6 показаны графики зависимости 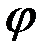 от
от 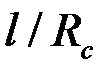 при трех значениях отношения
при трех значениях отношения 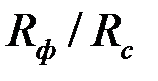 и
и 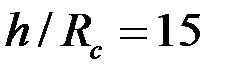 . Из него следует, что с увеличением
. Из него следует, что с увеличением 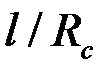 функция
функция 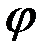 быстро растет до асимптотического значения, которое наступает при
быстро растет до асимптотического значения, которое наступает при 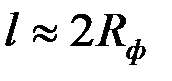 . Это доказывает нецелесообразность установки фильтра высотой больше чем
. Это доказывает нецелесообразность установки фильтра высотой больше чем 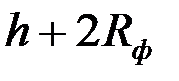 .
.
Влияние мощности пласта на 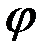 иллюстрируется графиками на рис.3.7 при тех же значениях
иллюстрируется графиками на рис.3.7 при тех же значениях 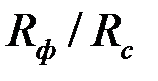 и
и 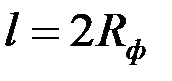 .
.
Лекция 5 § 6. МГНОВЕННЫЕ УРАВНЕНИЯ СОСТОЯНИЯ И
КРИТЕРИИ ПРОЧНОСТИ
1. Характерные мгновенные свойства твердых тел
при кратковременном осевом растяжении (сжатии).
На примере кратковременного осевого растяжения (сжатия) цилиндрического образца легко проследить характерные мгновенные свойства твердых тел. На рис. 12 показан общий вид деформационной кривой напряжение – деформация ( 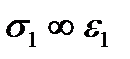 ). Эту кривую условно разбивают на следующие характерные участки:
). Эту кривую условно разбивают на следующие характерные участки:
ОА – участок упругих деформаций, где материал подчиняется линейному закону Гука
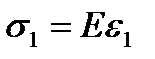 (2.66)
(2.66)
с коэффициентом пропорциональности Е, называемым модулем упругости, или модулем Юнга;
АВ – участок пластического течения (или текучести), характеризуемым нарастанием деформации или неизменном напряжении 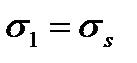 , которое называется пределом упругости или пределом текучести;
, которое называется пределом упругости или пределом текучести;
ВС – участок упрочнения, где нелинейная зависимость между напряжением и деформацией по аналогии с уравнение (2.56) представима в форме
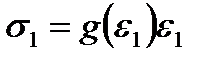 (2.67)
(2.67)
с коэффициентом 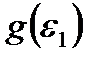 , называемым модулем пластичности;
, называемым модулем пластичности;
СD – участок разрушения, напряжение 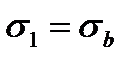 называется пределом прочности;
называется пределом прочности;
LM – участок разгрузки или повторной нагрузки.
Рис.12. Общий вид деформационной кривой
Если точка L расположена выше точки А, то при полной разгрузке исчезает накопленная упругая деформация 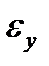 и сохраняется деформация пластическая
и сохраняется деформация пластическая 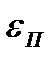 . При повторном нагружении образца его диаграмма мало отличается от кривой MLC, т.е. материал в результате первоначального нагружения выше
. При повторном нагружении образца его диаграмма мало отличается от кривой MLC, т.е. материал в результате первоначального нагружения выше 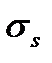 как бы приобретает дополнительные упругие свойства и повышает предел упругости
как бы приобретает дополнительные упругие свойства и повышает предел упругости 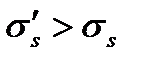 ; это явление называется упрочнением.
; это явление называется упрочнением.
Функцию 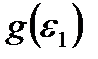 удобно задавать в аналитической форме, при выборе которой необходимо руководствоваться соображениями удобства при расчетах.
удобно задавать в аналитической форме, при выборе которой необходимо руководствоваться соображениями удобства при расчетах.
Экспериментально установлено, что степенной закон
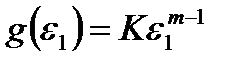 (2.68)
(2.68)
является часто наиболее приемлемым, где К и т – константы материала при испытаниях в заданных условиях.
Рис. 13. Деформационные кривые сухой глины
(1, 2, 3 – соответственно при  = 92, 29,13 МПа
= 92, 29,13 МПа
В качестве примера на рис.13 показаны диаграммы 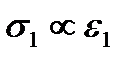 , построенные для высушенной на воздухе глины при нескольких значения всестороннего давления
, построенные для высушенной на воздухе глины при нескольких значения всестороннего давления  , в табл. 1 – результаты обработки этих диаграмм.
, в табл. 1 – результаты обработки этих диаграмм.
Таблица 1
 , МПа , МПа
| Е, 103, МПа | 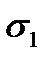 , МПа , МПа
| 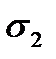 , МПа , МПа
| K, МПа | m | 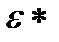 , % , %
|
| 0,4 | ||||||
| 1,1 | 0,4 | |||||
| 0,4 |
( 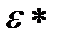 - общая деформация до разрушения)
- общая деформация до разрушения)
Параметры K и т определялись следующим образом. Кривые на рис. 13 перестраивались в логарифмических координатах 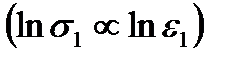 , и после сравнения полученной прямой с зависимостью
, и после сравнения полученной прямой с зависимостью 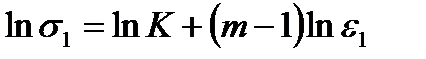 определялись искомые параметры.
определялись искомые параметры.
При осевом нагружении цилиндрического образца изменяется и его поперечный размер, определяемый деформацией 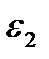 .
.
Величина v, равная отношению абсолютных значений поперечной деформации 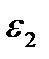 к продольной
к продольной 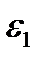 в упругой области при осевом нагружении образца, называется коэффициентом Пуассона.
в упругой области при осевом нагружении образца, называется коэффициентом Пуассона.
Способность твердых тел сжиматься (уплотняться) или расширяться (разуплотняться) устанавливается диаграммой всестороннее давление – объемная деформация 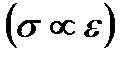 . Экспериментально установлено, что в широком диапазоне давлений зависимость
. Экспериментально установлено, что в широком диапазоне давлений зависимость 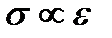 можно принимать в виде
можно принимать в виде
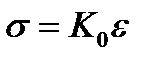 (2.69)
(2.69)
где 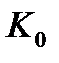 - модуль объемного сжатия или расширения в зависимости от вида нагружения.
- модуль объемного сжатия или расширения в зависимости от вида нагружения.
Определение модуля 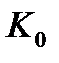 эквивалентно определению коэффициента Пуассона v, так как они связаны зависимостью
эквивалентно определению коэффициента Пуассона v, так как они связаны зависимостью
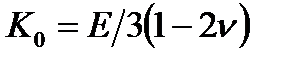 . (2.70)
. (2.70)
Отсюда, в частности, следует, что для реальных тел коэффициент Пуассона не может превосходить значения 0,5, т.е. 0 < v < 0,5.
Если для какого-либо тела можно принять v = 0,5, то такое идеальное тело принято называть несжимаемым, так как согласно (2.70), 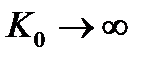 .
.
Рис. 14. Возможные виды деформационных кривых и соответствующие им формы разрушений для образцов горных пород
Деформационная кривая  может иметь разнообразный вид в зависимости от свойств материала и внешних условий. По этой кривой находят не только основные механические параметры тела, но и устанавливают определяющее его свойство – меру пластичности. Существуют различные классификации тел. Рекомендуется, например, следующая, довольно полная классификация горных пород [Справочник физических констант горных пород под редакцией С. Кларка]:
может иметь разнообразный вид в зависимости от свойств материала и внешних условий. По этой кривой находят не только основные механические параметры тела, но и устанавливают определяющее его свойство – меру пластичности. Существуют различные классификации тел. Рекомендуется, например, следующая, довольно полная классификация горных пород [Справочник физических констант горных пород под редакцией С. Кларка]:
а) очень хрупкая (рис.14, кривая 1), когда деформация, по существу, упругая до внезапного разрыва, характеризуемого образованием трещин отрыва перпендикулярно к наименьшему главному напряжению; накопленная при этом деформация не выше 1%;
б) хрупкая (кривая 2), когда наблюдается малая пластическая деформация до разрыва и образуются трещины отрыва и скола; накопленная деформация составляет 1 – 5%;
в) умеренно хрупкая (кривая 3), когда поведение промежуточное между хрупким и текучим, пик обозначает нарушение без общей потери связности, а разрушение происходит в результате образования трещин скола; накопленная деформация составляет 2 – 8%;
г) умеренно пластическая (кривая 4), когда разрушение сопровождается рассеянной деформацией, а накопленная деформация составляет 5 – 10%;
д) идеально пластическая (кривая 5), когда хорошо выражен предел текучести, сменяющийся постоянным однородным течением; деформация до разрыва более 10%;
е) пластическая с упрочнением (кривая 6), когда предел текучести может быть плохо выражен и процесс сопровождается работой упрочнения; деформация до разрыва более 10%.
Принадлежность горной породы к одному из приведенных типов определяет расчетную математическую модель и предельное состояние. В принципе, этой классификацией можно пользоваться при изучении любого твердого тела.
Среднестатистические значения опытных величин 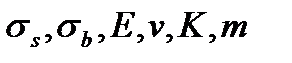 , соответствующие различным видам (сжатие, растяжение, изгиб, сдвиг) и условиям (температура, давление, влажность, скорости нагружения и др.) испытаний, принимаются в качестве основных механических параметров при кратковременных нагружениях изотропных твердых тел. Важной задачей экспериментального исследования является установление аналитической зависимости этих параметров от указанных факторов.
, соответствующие различным видам (сжатие, растяжение, изгиб, сдвиг) и условиям (температура, давление, влажность, скорости нагружения и др.) испытаний, принимаются в качестве основных механических параметров при кратковременных нагружениях изотропных твердых тел. Важной задачей экспериментального исследования является установление аналитической зависимости этих параметров от указанных факторов.
Многочисленными испытаниями установлено, что рост всестороннего давления и скорости деформирования способствует увеличение параметров 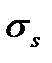 и
и 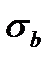 и переходу от хрупкого поведения к пластическому, а рост температуры и влажности, снижая предел текучести, препятствует образованию трещин и усиливает текучесть без заметного изменения формы деформационной кривой
и переходу от хрупкого поведения к пластическому, а рост температуры и влажности, снижая предел текучести, препятствует образованию трещин и усиливает текучесть без заметного изменения формы деформационной кривой 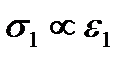 . Особое значение эти зависимости имеют для горных пород.
. Особое значение эти зависимости имеют для горных пород.
В практике инженерных расчетов чаще других используется следующая эмпирическая зависимость предельного значения 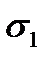 (
( 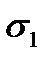 или
или 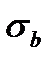 ) от среднего нормального напряжения
) от среднего нормального напряжения 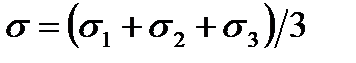 , предложенная Э. Хоеком:
, предложенная Э. Хоеком:
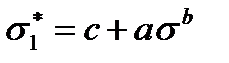 , (2.71)
, (2.71)
где с – значение 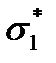 при
при 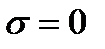 ; a, b – константы, являющиеся функциями температуры, влажности и др.
; a, b – константы, являющиеся функциями температуры, влажности и др.
При с = 0 получится зависимость, впервые предложенная Д. Франклином.
Для многих горных пород хорошей аппроксимацией может оказаться линейная зависимость, называемая критерием Мора,
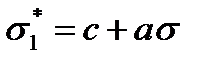 (2.72)
(2.72)
Примером влияния влажности W на механическую прочность пород может служит понтическая глина. Для этой глины линейная аппроксимация (2.72) вполне приемлема до давления  =50 МПа, а зависимость параметров с и а от влажности показана ниже.
=50 МПа, а зависимость параметров с и а от влажности показана ниже.
| W, % | ||||
| c, МПа | ||||
| а | 1,4 | 4,26 | 0,5 |
Инженерные расчеты удобно проводить, когда зависимость параметров с, а, b, равно как и K и т в формуле (2.68), от температуры и влажности принята в аналитической форме. Однако таких общепринятых норм в литературе не предложено. Поэтому необходимо руководствоваться соображениями удобства при расчетах с требуемой точностью. Например, в формуле (2.68) часто бывает удобным фиксировать показатель т, а коэффициент K считать линейной функцией, или экспонентой.
2. Упругое деформирование изотропных тел
при сложно-напряженном состоянии.
При сложно-напряженном состоянии упругое деформирование изотропных тел описывается общими уравнениями состояния, называемыми обобщенным законом Гука:
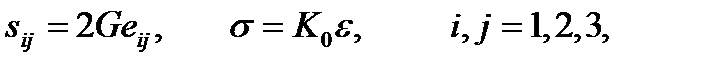 (2.73)
(2.73)
т.е. компоненты девиаторов напряжений и деформаций, среднее нормальное напряжение и относительное изменение объема пропорциональны или в эквивалентной форме:
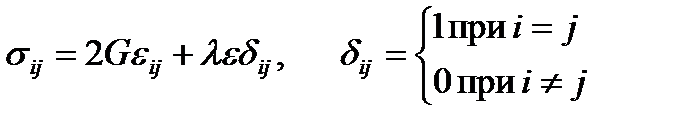 (2.74)
(2.74)
т.е. компоненты тензора напряжений суть линейные функции компонент тензора деформаций и обратно:
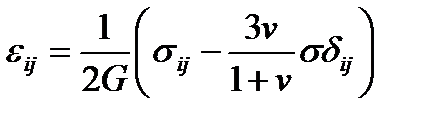 (2.75)
(2.75)
где 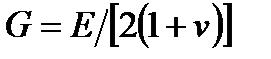 - модуль сдвига;
- модуль сдвига; 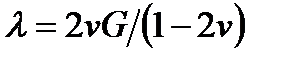 - коэффициент Ламе. Характерно, что коэффициенты пропорциональности в этих общих уравнения определяют параметрами, получаемым при простых видах нагружения.
- коэффициент Ламе. Характерно, что коэффициенты пропорциональности в этих общих уравнения определяют параметрами, получаемым при простых видах нагружения.
На основании уравнений (2.73) и формул (1.21), (1.40) выведено полезное соотношение
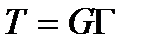 , (2.73/)
, (2.73/)
т.е. интенсивность касательных напряжений Т пропорциональна интенсивности деформаций сдвига Г.
Более сложными уравнениями описывается неупругая деформация. В приложениях обычно пользуются упрощенными теориями пластичности.
Наиболее широкое применение получили уравнения состояния деформационной теории пластичности
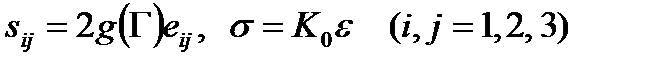 (2.76)
(2.76)
или в эквивалентной форме
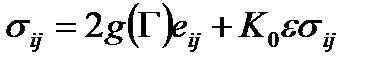 , (2.77)
, (2.77)
и обратная зависимость
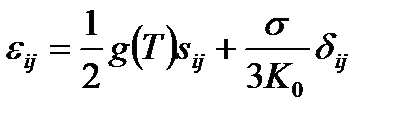 , (2.78)
, (2.78)
которые являются простым обобщением уравнений (2.73) – (2.75).
В уравнениях (2.76) – (2.78) функция g(Г) в силу соотношения 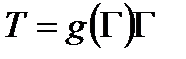 и формулы (2.67) определяется по виду функции
и формулы (2.67) определяется по виду функции 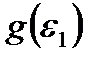 , например, подобно формуле (2.68):
, например, подобно формуле (2.68):
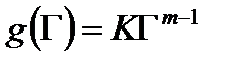 .
.
Функция 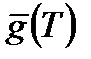 служит коэффициентом в обратном соотношении
служит коэффициентом в обратном соотношении 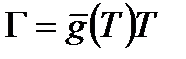 : например, для степенного закона (2.68)
: например, для степенного закона (2.68)
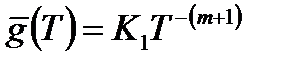 ,
,
где 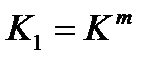 .
.
В случае несжимаемого тела (v = 0,5) уравнения состояния принимают вид
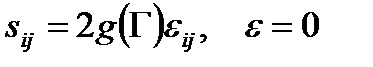 .
.
В состояния пластического течения (см. рис.12 участок АВ), например, при обобщенном критерии Губера – Мизеса, характеризующим переход к пластическим деформациям,
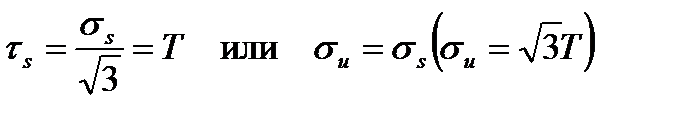 , (2.79)
, (2.79)
в уравнениях (2.76) и (2.77) функцию g(Г) необходимо принять 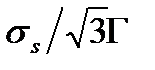 или
или 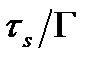 , где
, где 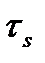 - интенсивность напряжений [см. формулу (1.41)]. В этом случае нельзя однозначно определить компоненты деформации
- интенсивность напряжений [см. формулу (1.41)]. В этом случае нельзя однозначно определить компоненты деформации 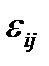 , подобно формуле (2.78), что вполне естественно, если обратить внимание на участок АВ (см. рис. 12), где нет взаимно однозначного соответствия между
, подобно формуле (2.78), что вполне естественно, если обратить внимание на участок АВ (см. рис. 12), где нет взаимно однозначного соответствия между 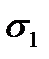 и
и 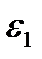 .
.
3. Критерий прочности
при кратковременном монотонном нагружении.
Критерий прочности при кратковременном монотонном нагружении – это есть условие перехода какого-либо элемента нагруженного твердого тела в состояние хрупкого разрушения или пластического течения, когда в известной мере исчерпывается несущая способность. При одноосном напряженном состоянии критерий прочности оценивается предельным, или опасным, значением напряжения; например, на рис. 12 это 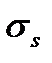 или
или 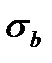 . При переходе к сложному напряженному состоянию исходят из простейшего естественного предположения: уравнение предельного состояния не должно зависеть от выбора системы координат и должно содержать лишь инварианты, характеризующие напряженное состояние. Согласно выводам лекции 1.2, этими инвариантами будут T – интенсивность касательных напряжений;
. При переходе к сложному напряженному состоянию исходят из простейшего естественного предположения: уравнение предельного состояния не должно зависеть от выбора системы координат и должно содержать лишь инварианты, характеризующие напряженное состояние. Согласно выводам лекции 1.2, этими инвариантами будут T – интенсивность касательных напряжений;  - среднее нормальное напряжение;
- среднее нормальное напряжение; 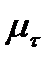 - параметр Лоде – Надаи. Поэтому в общем случае критерий прочности определяется некоторой предельной поверхностью
- параметр Лоде – Надаи. Поэтому в общем случае критерий прочности определяется некоторой предельной поверхностью 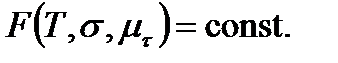
Предложено много различных критериев прочности при сложно-напряженном состоянии изотропных тел. В инженерных расчетах чаще других применяют критерий Шлейхера – Надаи
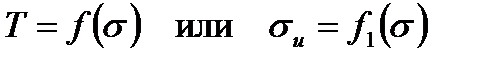 , (2.80)
, (2.80)
где вид функции в правой части устанавливается экспериментально по данным опытов для конкретных материалов.
В частности, при 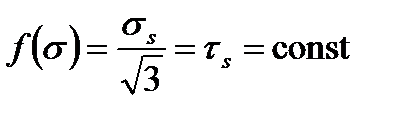 из (2.70) следует критерий Губера – Мизеса (2.79) или эквивалентный ему по форме энергетический критерий. Оба этих критерия основаны на гипотезе, по которой процесс разрушения зависит главным образом от изменения формы элемента тела.
из (2.70) следует критерий Губера – Мизеса (2.79) или эквивалентный ему по форме энергетический критерий. Оба этих критерия основаны на гипотезе, по которой процесс разрушения зависит главным образом от изменения формы элемента тела.
При достижении потенциальной энергией формоизменения элемента тела предельного состояния наступает его разрушение или переход к пластической деформации.
Если 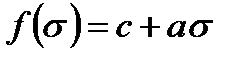 , то из условия (2.80) следует обобщенный критерии Мора
, то из условия (2.80) следует обобщенный критерии Мора 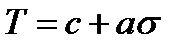 . Используя формулы разд.2, критерий (2.80) можно сформулировать в терминах максимального касательного
. Используя формулы разд.2, критерий (2.80) можно сформулировать в терминах максимального касательного 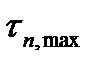 и нормального
и нормального 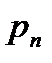 напряжений:
напряжений:
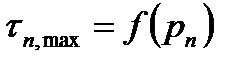 .
.
Например, относительно главных координатных осей при условии 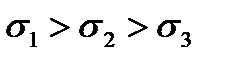 , обобщая соотношение (2.71), можно принять
, обобщая соотношение (2.71), можно принять
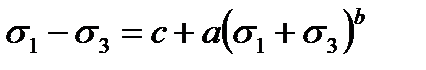 .
.
Иногда в качестве критерия разрушения используются ограничения деформаций.
Изучая механическое поведение горных пород, надо иметь в виду присущие им важные особенности: с одной стороны, деформационную и прочностную анизотропию, обусловленную слоистостью, сланцеватостью или направленной трещиноватостью их строения, а с другой – наличием пор или трещин, заполненных пластовой жидкостью, газом или их смесью.
4. Трансверсально-изотропные тела (свойства анизотропии горных пород в плоскости, параллельной напластованию).
При изучении анизотропии горных пород чаще всего ограничиваются изучением свойств горных пород в плоскости, параллельной напластованию, и плоскости, перпендикулярной к напластованию, считаю любое из направлений в этих плоскостях эквивалентным в отношении механических свойств.
Такие тела принято называть трансверсально-изотропными. Ниже приведены упругие постоянные некоторых горных пород, заимствованные из разных литературных источников: Е, Е’ – модули Юнга по направлениям, параллельным напластованию и перпендикулярным к ним; v, v’ – коэффициенты Пуассона, характеризующие поперечное сжатие в плоскости напластования при сжатии в той же плоскости и в направлении, перпендикулярном к ней.
Если координатная плоскость 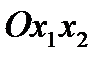 выбрана параллельно плоскости напластования, а ось
выбрана параллельно плоскости напластования, а ось 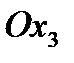 - перпендикулярно к ней, то обобщенный закон Гука записывается в виде:
- перпендикулярно к ней, то обобщенный закон Гука записывается в виде:
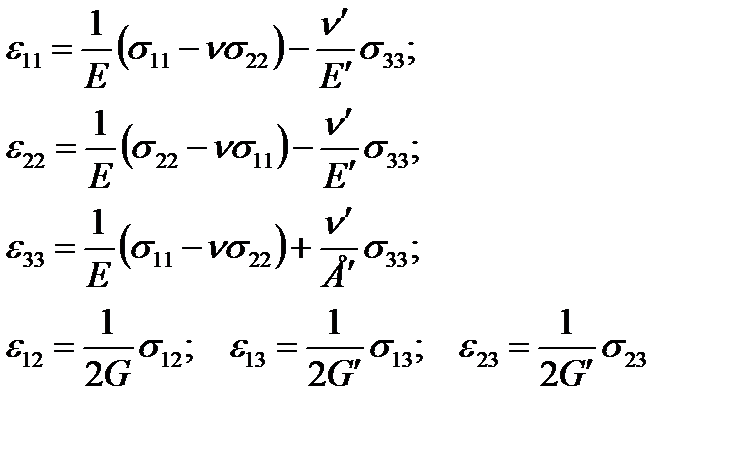 (2.81)
(2.81)
где 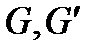 - модули сдвига в плоскости
- модули сдвига в плоскости 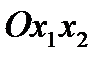 и в перпендикулярных к ней плоскостях.
и в перпендикулярных к ней плоскостях.
| Упругие постоянные горных пород | 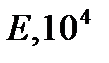 МПа МПа
| 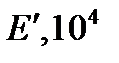 МПа МПа
| 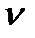
| 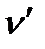
|
| Алевролит | 6,21 | 5,68 | 0,29 | 0,26 |
| Глинистые сланцы | 3,16 | 1,54 | 0,22 |
Дата добавления: 2015-12-11; просмотров: 5625; |
Генерация страницы за: 0.189 сек.

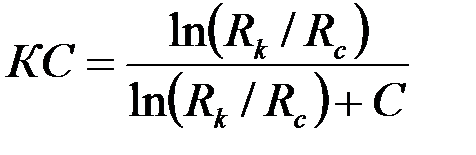 .
.
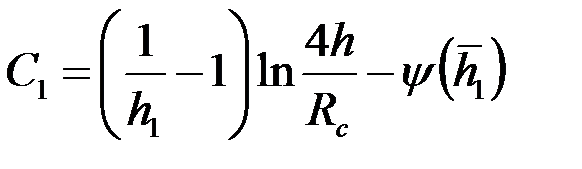 .
.
