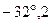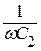Линейные электрические цепи однофазного синусоидального тока
1.1 Основные теоретические сведения.
1. Гармоническим током называют переменный периодический ток, изменяющийся во времени по синусоидальному (косинусоидальному) закону (рис.1).
 Мгновенное значение гармонического тока (напряжения, ЭДС):
Мгновенное значение гармонического тока (напряжения, ЭДС):
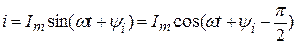 ,
,
где Im - амплитуда гармонического тока (максимальное значение), А;
w = 2pf - угловая частота (скорость изменения фазы тока), с−1;
f = 1/T - частота (число периодов в секунду), Гц;
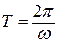 - период (время одного полного колебания), с;
- период (время одного полного колебания), с;
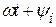 - фаза (аргумент синусоидального (косинусоидального) тока, отсчитываемый от точки перехода тока через нуль (максимум) к положительному значению), рад;
- фаза (аргумент синусоидального (косинусоидального) тока, отсчитываемый от точки перехода тока через нуль (максимум) к положительному значению), рад;
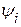 - начальная фаза (значение гармонически изменяющегося тока в начальный момент времени t = 0), рад.
- начальная фаза (значение гармонически изменяющегося тока в начальный момент времени t = 0), рад.
2. Среднее значение гармонически изменяющегося тока (напряжения ЭДС) - значение, соответствующее положительной полуволне:
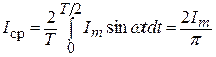 .
.
Действующее значение гармонически изменяющегося тока (напряжения ЭДС) - среднеквадратичное значение за период:
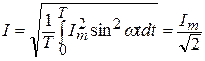 .
.
Коэффициент амплитуды:
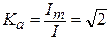 .
.
Коэффициент формы:
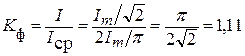 .
.
3. Мгновенные значения напряжений источников ЭДС, токов источников тока можно заменить соответствующими комплексными значениями:
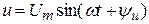 заменяют на
заменяют на 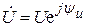 ;
;
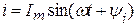 заменяют на
заменяют на 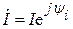 .
.
Комплексное сопротивление цепи:
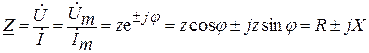 ,
,
где 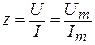 - отношение действующего или амплитудного напряжения к действующему или амплитудному току, называют полным сопротивлением цепи, равным модулю комплексного сопротивления (абсолютная величина |
- отношение действующего или амплитудного напряжения к действующему или амплитудному току, называют полным сопротивлением цепи, равным модулю комплексного сопротивления (абсолютная величина | 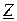 |).
|).
С другой стороны:
(zcosj + jzsinj)×(zcosj – jzsinj) = (R + jX)×(R – jX) Þ 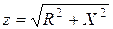 .
.
Величины R + jX и R - jX называют сопряженными.
Аргументом служит угол между осью действительных значений и вектором изображающим комплексную величину и равный разности начальных фаз напряжения и тока: 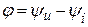 .
.
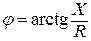 .
.
Комплексная проводимость цепи:
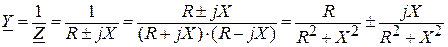 .
.
Положив
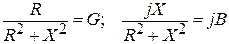 ,
,
получим
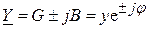 ,
,
где 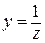 − полная проводимость цепи.
− полная проводимость цепи.
С другой стороны:
(ycosj + jysinj)×(ycosj − jysinj) = (G + jB)×(G − jB) Þ 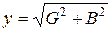 .
.
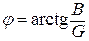 .
.
4. Мгновенная мощность цепи:
p = ui = Umsinwt × Imsin(wt – j) = UIcosj – UIcos(2wt – j),
где начальная фаза напряжения 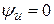 , а начальная фаза тока
, а начальная фаза тока 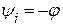 .
.
Активная мощность - среднее значение мгновенной мощности за период:
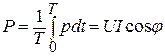 .
.
Полная мощность - произведение действующих значений напряжения и тока:
S = UI.
Коэффициент мощности - отношение активной мощности к полной:
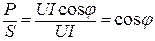 .
.
Реактивная мощность:
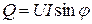 ,
,
положительна при j > 0 и отрицательна при j < 0.
Активную, полную и реактивную мощности связывают соотношения:
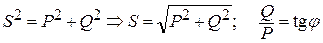 .
.
5. Законы Ома и Кирхгофа в комплексной форме:
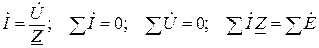 .
.
1.1
|
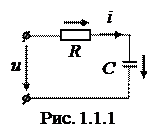 |
|
|
Определить
Вычислить мгновенные значения напряжений на резисторе, на конденсаторе, приложенного напряжения и мощности. Построить графики мгновенных значений тока, напряжений и мощности.
Решение
Поскольку в условии не оговаривается начальная фаза тока, то его мгновенное значение равно:
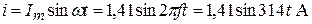 .
.
Мгновенное значение напряжения на резисторе:
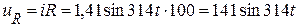 B.
B.
Мгновенное значение напряжения на конденсаторе:
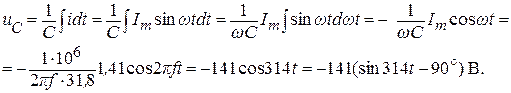
Мгновенное значение приложенного напряжения:
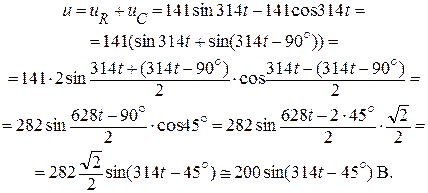
Последнее выражение можно также получить, исходя из следующих рассуждений.
Полное сопротивление цепи равно:
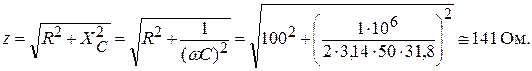
Находим аргумент:
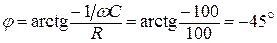 .
.
Поскольку j < 0, то приложенное напряжение u отстает от тока i по фазе на соответствующий угол.
Амплитуда приложенного напряжения:
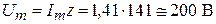 .
.
Следовательно
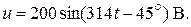
Находим мгновенную мощность цепи:
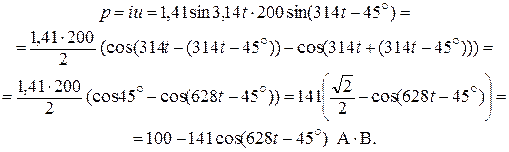
Графики мгновенных значений, построенные в произвольном масштабе, приведены на рис. 1.1.2.
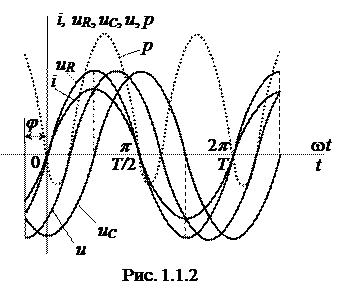
Из графика видно, что ток i и напряжение 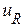 на активном сопротивлении совпадают по фазе, а напряжение
на активном сопротивлении совпадают по фазе, а напряжение 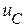 на конденсаторе отстает от тока i на 90о.
на конденсаторе отстает от тока i на 90о.
1.2
Дано
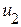
|
Определить
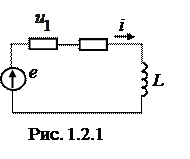
Ток и напряжение на элементах схемы рис. 1.2.1, методами комплексных амплитуд и мгновенных величин. Проверить баланс мощностей. Построить векторную диаграмму.
Решение
Для мгновенного и действующего значений ЭДС справедливы соотношения:
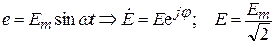 .
.
Находим комплексное сопротивление цепи:
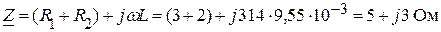 .
.
Находим модуль и аргумент комплексного числа:
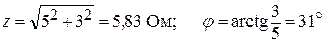 .
.
Откуда
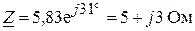 .
.
Тогда комплексное действующее значение тока:
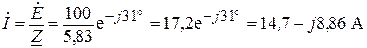 .
.
Комплексное действующее значение напряжения на сопротивлении R1:
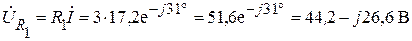 .
.
Комплексное действующее значение напряжения на сопротивлении R2:
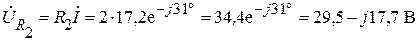 .
.
Комплексное напряжение на индуктивности:
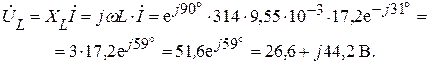
Таким образом, напряжение на индуктивности опережает ток на угол 90о:
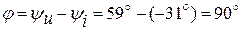 .
.
Согласно закону Ома мгновенное значение тока:
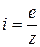 ,
,
где
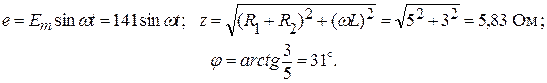
Тогда
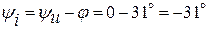 .
.
Амплитудное значение тока:
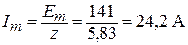 .
.
Откуда
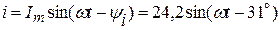 А.
А.
Находим мгновенное значение напряжения на сопротивлении R1:
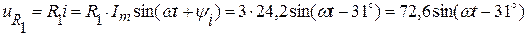 B.
B.
Находим мгновенное значение напряжения на сопротивлении R2:
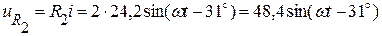 B.
B.
Мгновенное значение напряжения на индуктивности:
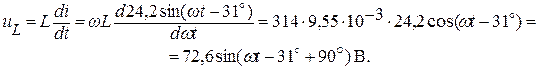
Таким образом, напряжение на индуктивности опережает ток на угол 90о.
Баланс мощностей следует из закона сохранения энергии, т.е. сумма всех отдаваемых мощностей равна сумме всех потребляемых мощностей:
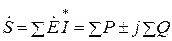 ,
,
где 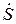 - комплексная мощность;
- комплексная мощность;
P - активная мощность;
Q - реактивная мощность;
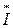 - комплексно – сопряженная величина.
- комплексно – сопряженная величина.
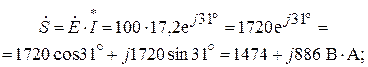
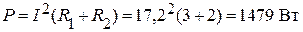 ;
;
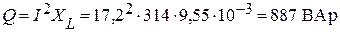 .
.
Здесь 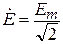 ;
; 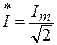 .
.
Таким образом, с незначительной погрешностью активная и реактивная мощности совпадают с вещественной и мнимой частями комплексной мощности.
На комплексной плоскости строим векторную диаграмму рис.1.2.2.
| |||||||||
| |||||||||
| |||||||||
| |||||||||
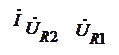 | |||||||||
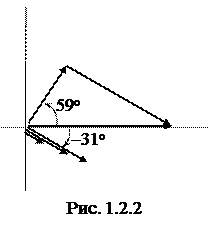 |
1.3

Определить
Действующий ток I, угол сдвига фаз между ЭДС источника и тока, напряжение на элементах схемы. Построить треугольники сопротивлений, напряжений и мощностей.
Решение
Находим индуктивное сопротивление катушки:
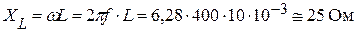 .
.
Находим емкостное сопротивление конденсатора:
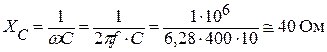 .
.
Полное сопротивление цепи:
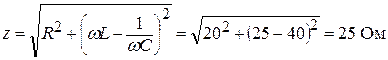 .
.
Находим угол сдвига фаз ЭДС и тока:
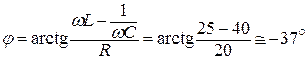 .
.
Ток I равен:
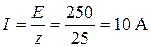 .
.
Находим напряжение на активном сопротивлении:
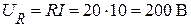 или
или 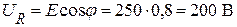 .
.
Напряжение на катушке индуктивности:
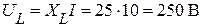 .
.
Напряжение на конденсаторе:
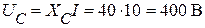 .
.
Реактивное сопротивление цепи (последовательное соединение катушки индуктивности и конденсатора):
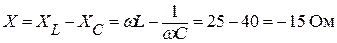 .
.
Или 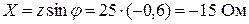 .
.
Тогда напряжение на реактивном сопротивлении цепи:
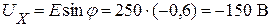 , или
, или 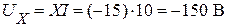 .
.
Активная мощность:
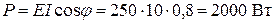 , или
, или 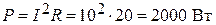 .
.
Реактивная мощность:
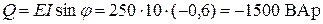 .
.
Или 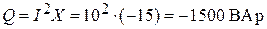 .
.
Полная мощность:
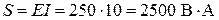 , или
, или 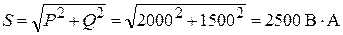 .
.
Согласно выполненным расчетам в произвольном масштабе строим треугольники сопротивлений, напряжений и мощностей рис.1.3.2.
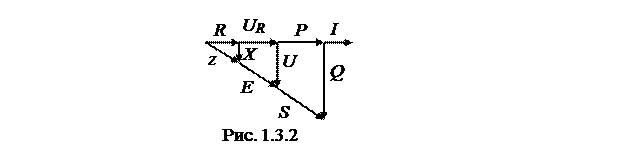
При XL = XC в электрической цепи (рис. 1.3.1) наступает резонанс напряжений, поскольку значения противоположных по фазе напряжений на индуктивности UL и емкости UC становятся равными.
1.4
Дано
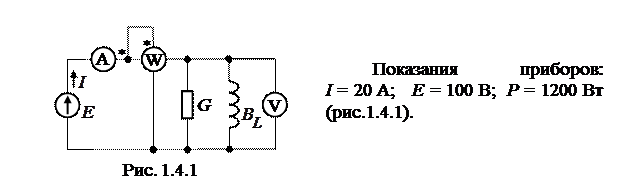
Определить
Составляющие тока I. Построить треугольники проводимостей и токов.
Решение
Найдем полную проводимость цепи:
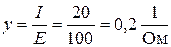 .
.
Находим активную проводимость:
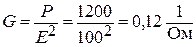 .
.
Вычислим реактивную проводимость:
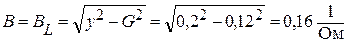
Находим угол сдвига фаз ЭДС и тока:
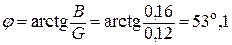 .
.
Находим активную составляющую тока:
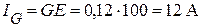 , или
, или 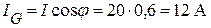 .
.
Вычислим реактивную составляющую тока:
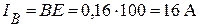 , или
, или 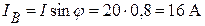 .
.
Согласно выполненным расчетам в произвольном масштабе строим треугольники проводимостей, и токов рис. 1.4.2.
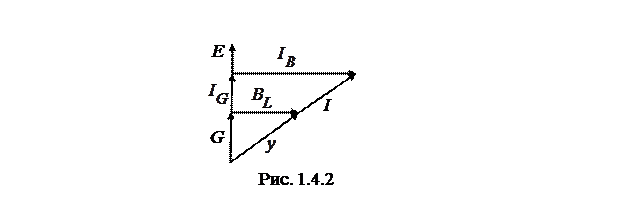
1.5
 Определить
Определить
Cоставляющие тока I. Построить треугольники проводимостей и токов.
Решение
Найдем полную проводимость цепи:
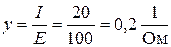 .
.
Находим активную проводимость:
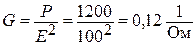 .
.
Вычислим реактивную проводимость:
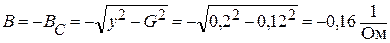 .
.
Находим угол сдвига фаз ЭДС и тока:
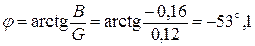 .
.
Находим активную составляющую тока:
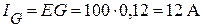 , или
, или 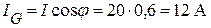 .
.
Вычислим реактивную составляющую тока:
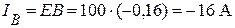 , или
, или 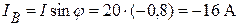 .
.
Согласно выполненным расчетам строим треугольники проводимостей, и токов (масштаб произвольный) рис. 1.5.2.
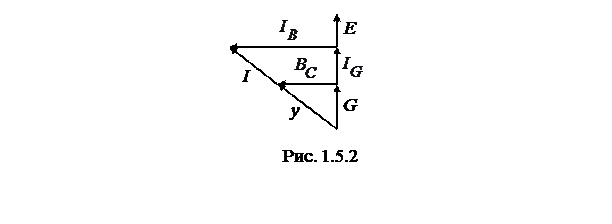 1.6
1.6
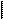 Дано
Дано
|
|
|
Определить
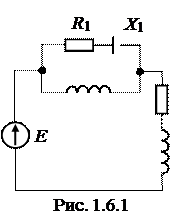
Полные, активные и реактивные сопротивления (проводимости) всей цепи и всех ветвей рис. 1.6.1. Токи, напряжения и мощности. Проверить баланс мощностей. Построить векторную диаграмму напряжений и токов. Задачу решить аналитическим методом.
Решение
Найдем полные сопротивления каждой из трех ветвей цепи:
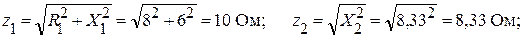
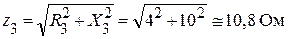 .
.
Активную и реактивную проводимости этих ветвей найдем по переходным формулам:
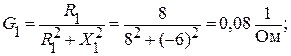
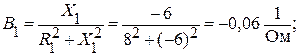
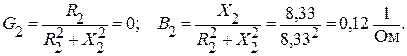
Полные проводимости первой и второй ветвей:
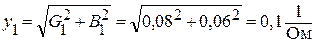 , или
, или 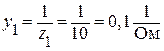 ;
;
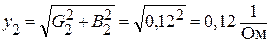 , или
, или 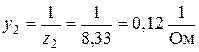 .
.
Находим активную и реактивную проводимости параллельно соединенных ветвей:
G = G1 + G2 = 0,08 + 0 = 0,08 1/Ом; B = B1 + B2 = –0,06 + 0,12 = 0,06 1/Ом.
Полная проводимость параллельно соединенных ветвей:
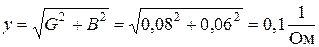 .
.
При последовательном соединении разветвленного участка цепи и третьей ветви сопротивление всей цепи определится как сумма сопротивлений этих участков. Поэтому по переходным формулам вычислим активное и реактивное сопротивления разветвленного участка цепи:
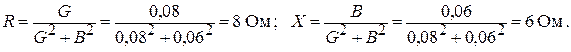
Находим полное сопротивление разветвленного участка цепи:
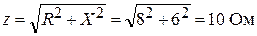 .
.
Вычислим активное и реактивное сопротивление всей цепи:
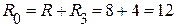 Ом;
Ом; 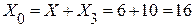 Ом.
Ом.
Находим полное сопротивление всей цепи:
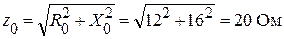 .
.
Ток всей цепи (или ток в третьей ветви) равен:
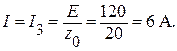
Находим разность фаз между э.д.с. и током цепи:
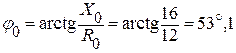 .
. 
Тогда напряжение третьей ветви:
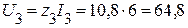 B.
B.
Вычислим активную и реактивную составляющие напряжения U3:
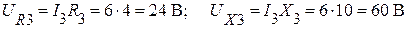 .
.
В качестве проверки:
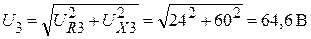 .
.
Расхождение (относительная ошибка) составляет ≈ 0,3% .
Находим разность фаз между напряжением U3 и током I3:
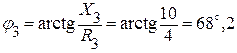 .
.
Найдем напряжение разветвленного участка цепи:
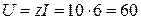 B.
B.
Разность фаз между напряжением U и током I:
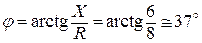 .
.
Находим токи первой и второй ветвей разветвленного участка:
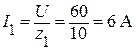 , или
, или 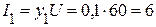 A;
A;
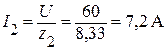 , или
, или 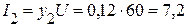 A.
A.
Вычислим активные и реактивные составляющие этих токов:
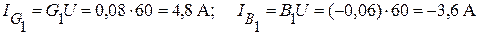 .
.
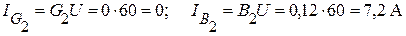 .
.
В качестве проверки:
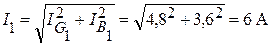 ;
; 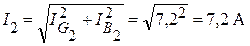 .
.
Находим разность фаз между напряжением U и токами I1 и I2:
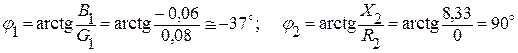 .
.
Определяем активную мощность всей цепи:
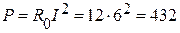 Вт .
Вт .
Находим реактивную мощность всей цепи:
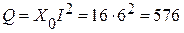 BAр .
BAр .
Полная мощность всей цепи:
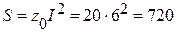 В×A .
В×A .
Вычислим активную, реактивную и полную мощности первой ветви разветвленного участка:
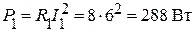 ;
; 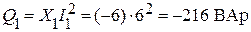 ;
; 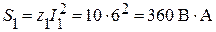 .
.
Вычислим активную, реактивную и полную мощности второй ветви разветвленного участка:
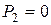 ;
; 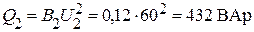 ;
;
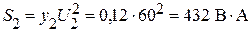 .
.
Вычислим активную, реактивную и полную мощности третьей ветви:
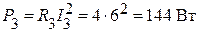 ;
; 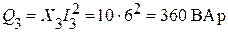 ;
; 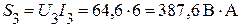 .
.
Баланс мощностей:
P = P1 + P2 + P3 Þ 432 = 288 + 0 + 144 Þ 432 Вт = 432 Вт;
Q = Q1 + Q2 + Q3 Þ 576 = –216 + 432 + 360 Þ 576 вар = 576 BAр;
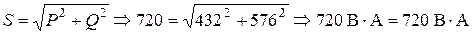 .
.
Векторную диаграмму рис. 1.6.2 строим в произвольно выбранном масштабе.
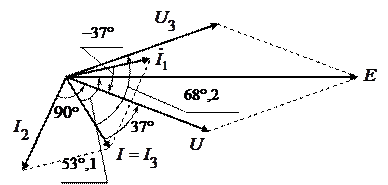 |
Рис. 1.6.2
1.7
|
Дано 
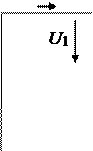 |

|

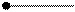
|
|







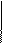


|
|
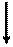
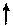
 C2 = 0,2×10−6Ф; f = 60 Гц.
C2 = 0,2×10−6Ф; f = 60 Гц.
 | |||||
 | |||||
 | |||||
Определить
Найти токи и напряжения схемы рис. 1.7.1, а также убедиться в достаточности мощности резистора R. Построить векторную диаграмму напряжений и токов.
Решение
Находим емкостное сопротивление конденсатора C1:
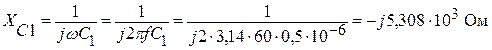 .
.
Находим емкостное сопротивление конденсатора C2:
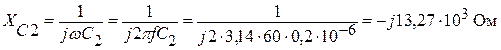 .
.
Вычислим сопротивление разветвленной части схемы:
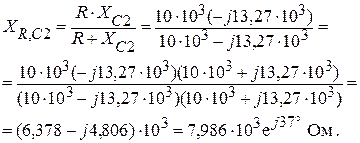
Находим сопротивление XAB всей цепи:
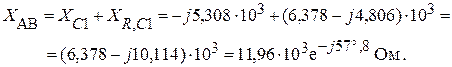
Тогда ток I1 будет равен:
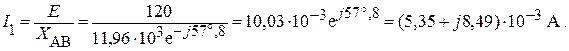
Находим напряжение U1:
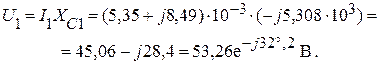
Найдем угол сдвига тока I1 относительно источника ЭДС E.
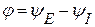 ,
,
где
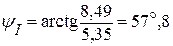 .
.
Тогда
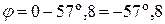 .
.
Найдем мощность рассеиваемую в цепи между точками А и В:
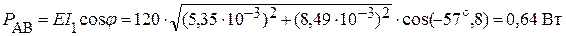 .
.
В данной цепи имеется только одно сопротивление R, в котором будет рассеиваться вся мощность. Убедиться в достаточности мощности сопротивления R можно также следующим образом:
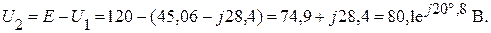
Тогда
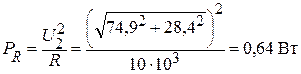 .
.
Выбранная по условию мощность PR = 1 Вт для сопротивления R,достаточна.
Найдем ток I3, протекающий через резистор R:
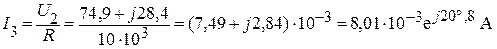 .
.
Найдем ток I2, протекающий через конденсатор С2:
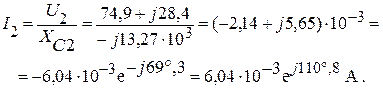
Выполним проверку вычисленных токов:
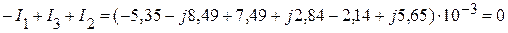 .
.
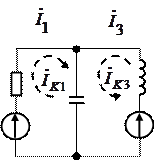
Искомые токи можно вычислить, применив к цепи рис. 1.7.1, например, метод контурных токов, положив, что IK1 = I1, а IK2 = I2. Тогда, система уравнений в матричной форме будет иметь вид:
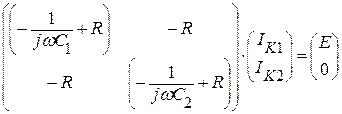 .
.
Главный определитель системы:
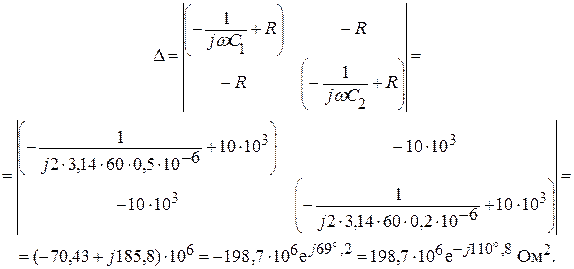
Произведя замену первого столбца главного определителя системы, столбцом свободных параметров получим:
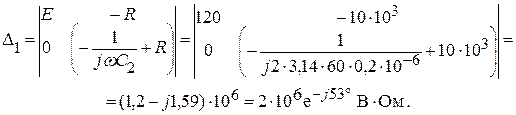
Находим контурный ток IK1 = I1:
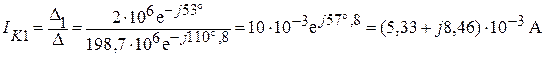 ,
,
что при незначительном расхождении совпадает с полученным выше результатом.
Произведя замену второго столбца главного определителя системы, столбцом свободных параметров получим:
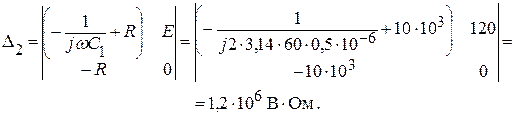
Находим контурный ток IK2 = I2:
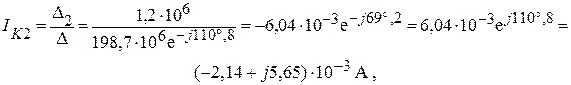
что совпадает с полученным выше результатом.
Ток I3, протекающий через резистор R, можно найти, воспользовавшись первым законом Кирхгофа, а напряжение U2 – законом Ома для участка цепи.
Строим векторную диаграмму рис. 1.7.2 (масштаб произвольный).
|

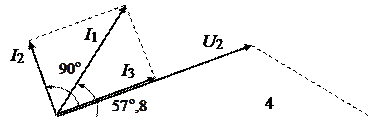
|
| |
1.8
 |
Дано
 |  | ||||||
| |||||||
| |||||||
|
|
|
|
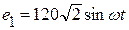 ;
; 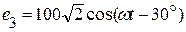 ;
; 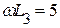 Ом;
Ом; 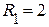 Ом;
Ом; 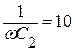 Ом.
Ом.
|
Определить
Токи и напряжения на элементах, применив метод контурных токов (рис. 1.8.1). Проверить баланс мощностей. Построить векторную диаграмму. Задачу решить методом комплексных амплитуд.
Решение
Система уравнений электрической цепи (рис. 1.8.1) в матричной форме:
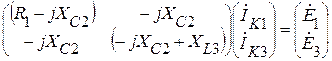 .
.
Вычислим главный определитель системы.
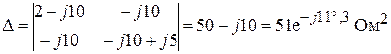 .
.
Произведя замену первого столбца главного определителя системы, столбцом свободных параметров, получим:
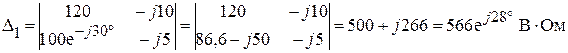 .
.
Находим величину контурного тока 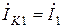 :
:
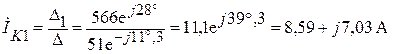 .
.
Произведя замену второго столбца главного определителя системы, столбцом свободных параметров, получим:
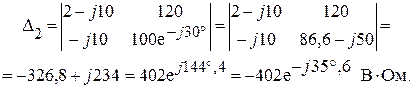
Находим величину контурного тока 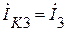 :
:
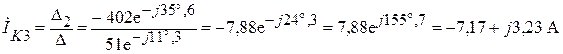 .
.
Вычислим ток 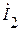 :
:
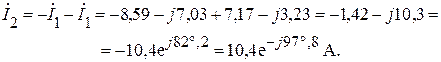
Найдем напряжение на резисторе R1:
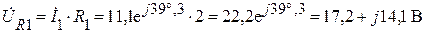 .
.
Ищем напряжение на конденсаторе С2:
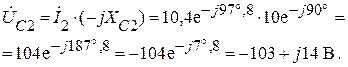
Ищем напряжение на катушке индуктивности L3:
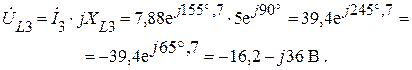
Проверяем баланс мощностей.
Комплексная мощность:
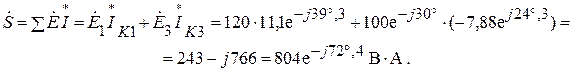
Активная мощность цепи:
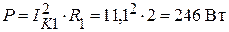 ,
,
или
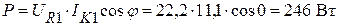 .
.
Реактивная мощность цепи (без j):
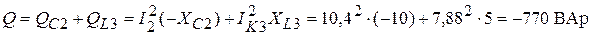 ,
,
или
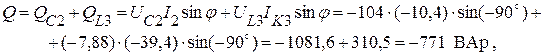
что при незначительных расхождениях совпадает с вещественной и мнимой частями комплексной мощности.
Строим векторную диаграмму рис. 1.8.2 (масштаб произвольный).
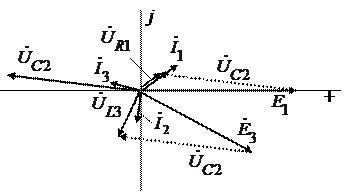 | |||
|
1.9
Дано
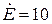 В;
В; 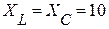 Ом;
Ом;  Ом.
Ом.

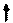














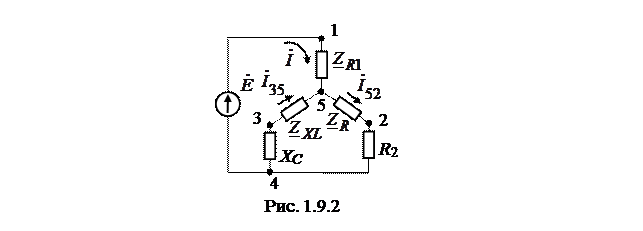
|
|
|
|
|
|
|
|
| |
| |
|

 Решение
Решение
|
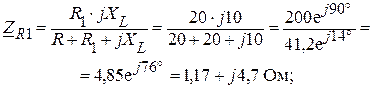
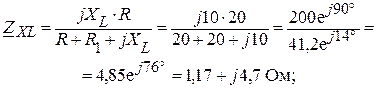
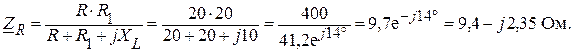
Напряжение холостого хода между точками 5 и 2 найдем из схемы согласно рис. 1.9.3.
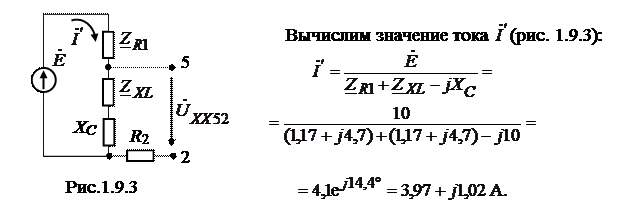
Тогда напряжение холостого хода найдем из закона Ома:
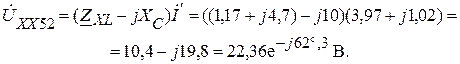
Входное сопротивление к точкам 5 и 2 найдем согласно схеме
рис. 1.9.4.
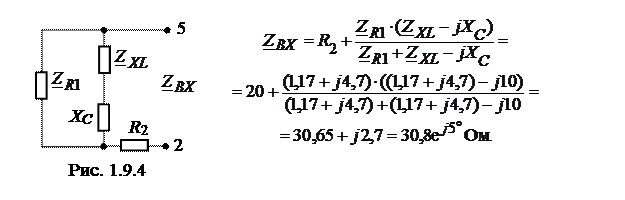
Теперь можем вычислить ток 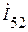 рис. 1.9.2:
рис. 1.9.2:
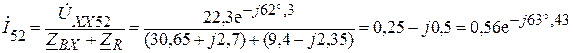 А.
А.
Найдем напряжение между узлами 5 и 2 схемы рис. 1.9.2:
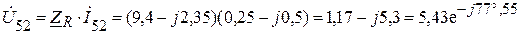 В.
В.
Напряжение холостого хода между точками 3 и 5 найдем из схемы согласно рис. 1.9.5.
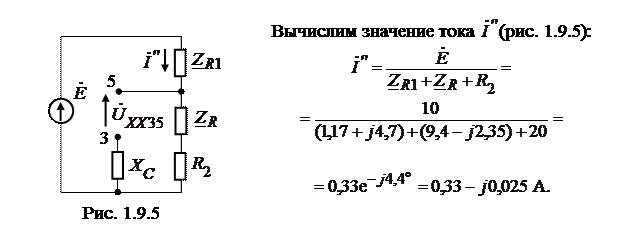
Тогда напряжение холостого хода найдем из закона Ома:
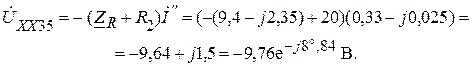
Входное сопротивление к точкам 3 и 5 найдем согласно схеме
рис. 1.9.6.
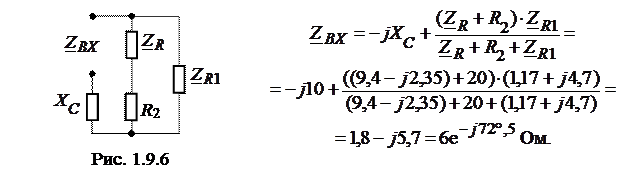
Вычислим ток 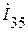 рис. 1.9.2:
рис. 1.9.2:
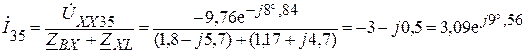 А.
А.
Найдем напряжение между узлами 3 и 5 схемы рис. 1.9.2:
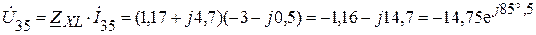 В.
В.
Теперь можем найти напряжение между точками 3 и 2 (рис. 1.9.2):
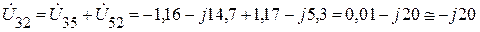 В.
В.
Наконец ток 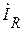 в сопротивлении R (рис. 1.9.1) будет равен:
в сопротивлении R (рис. 1.9.1) будет равен:
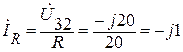 А.
А.
Таким образом, практически в сопротивлении R протекает чисто емкостной ток.
1.10
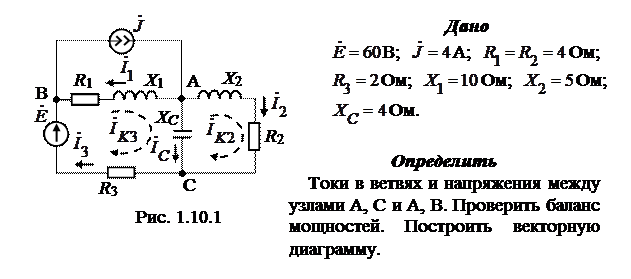
Решение
В контурных токах система уравнений для электрической цепи
рис. 1.10.1 будет иметь вид:
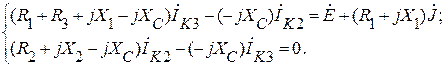
Или в матричной форме:
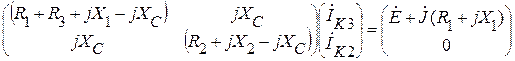 .
.
Раскрытие главного определителя системы дает:
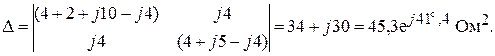
Произведя замену первого столбца в матрице коэффициентов, столбцовой матрицей свободных параметров получим:
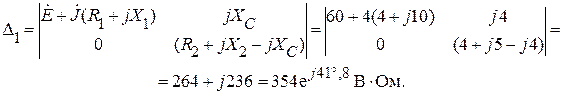
Произведя аналогичную замену для второго столбца в матрице коэффициентов, будем иметь:
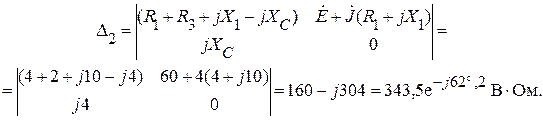
Тогда
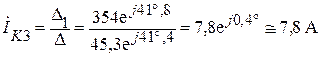 ;
;
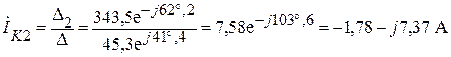 .
.
Ищем токи 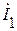 и
и 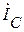 :
:
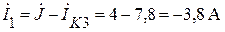 ;
;
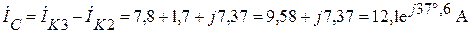 .
.
Найдем напряжение между узлами А, С.
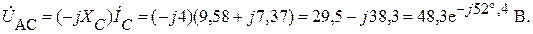
Найдем напряжение между узлами А, В.
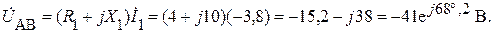
Баланс мощностей.
Комплексная мощность:
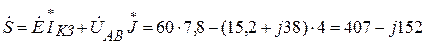
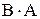 .
.
Активная мощность:
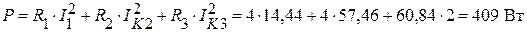 .
.
Реактивная мощность (без j):
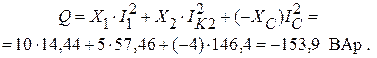
Расхождения в вычислениях мощностей ≈ 1,2%.
Строим векторную диаграмму рис. 1.10.2 (масштаб произвольный).
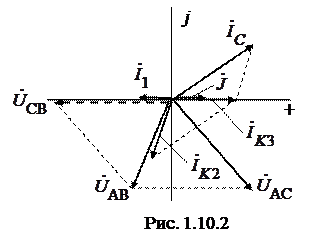 |
При необходимости напряжение 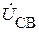 между узлами С и В найдем из второго закона Кирхгофа (на рис. 1.10.2 этот вектор показан пунктиром):
между узлами С и В найдем из второго закона Кирхгофа (на рис. 1.10.2 этот вектор показан пунктиром):
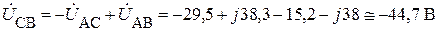 ,
,
или 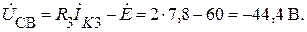
Расхождения в вычислениях ≈ 0,7%.
1.11
|

|


|
|










|


|

|

|


|
|


|

 |
Дано 
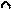
|
|
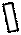


|
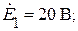
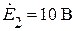 .
.
 |
|
 Определить
Определить
 Токи во всех ветвях, используя метод узловых потенциалов схемы рис. 1.11.1.
Токи во всех ветвях, используя метод узловых потенциалов схемы рис. 1.11.1.
Проверить баланс мощностей.
Построить векторную диаграмму токов.
Решение
Вычислим проводимости каждой из ветвей схемы рис. 1.11.1:
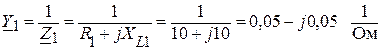 ;
;
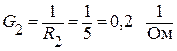 ;
; 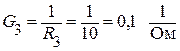 ;
;
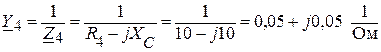 ;
;
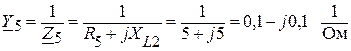 .
.
Вычислим общую проводимость 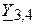 двух параллельно соединенных ветвей с проводимостями G3 и
двух параллельно соединенных ветвей с проводимостями G3 и 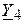 :
:
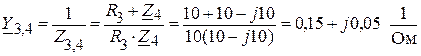 .
.
Найдем общую проводимость 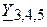 двух последовательно соединенных ветвей с проводимостями
двух последовательно соединенных ветвей с проводимостями 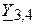 и
и 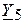 :
:
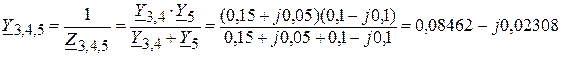
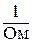 .
.
Тогда электрическую цепь рис. 1.11.1 можем преобразовать к виду рис. 1.11.2.

Вычислим потенциал 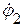 :
:
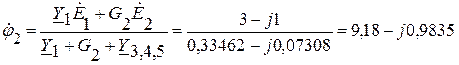 В.
В.
Находим значения токов ветвей схемы рис. 1.11.2:
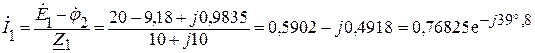 А;
А;
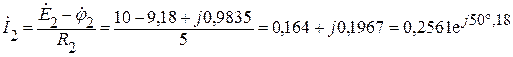 А;
А;
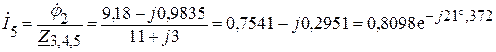 А.
А.
Можно убедиться, что сумма вычисленных токов в любом из узлов схемы рис. 1.11.2 равна нулю.
Для того чтобы найти токи 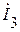 ,
, 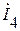 схемы рис. 1.11.1 вычислим напряжение между двумя параллельными ветвями по которым протекают упомянутые токи:
схемы рис. 1.11.1 вычислим напряжение между двумя параллельными ветвями по которым протекают упомянутые токи:
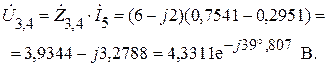
Находим токи