Электрические цепи, подключенные на периодическое несинусоидальное напряжение
4.1
 | |||
| |||
Определить
Мгновенное значение тока, показания приборов и мощность электрической цепи рис. 4.1.1.
Решение
Поскольку сопротивление конденсатора постоянному току равно бесконечности то составляющая тока I0 = 0.
Находим действующее значение тока первой гармоники, протекающего через конденсатор:
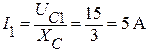 .
.
Ищем сопротивление конденсатора для третьей гармоники:
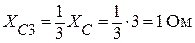 .
.
Действующее значение тока через конденсатор для третьей гармоники:
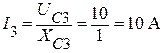 .
.
Найдем мгновенное значение тока электрической цепи, помня, что ток, протекающий через конденсатор, опережает напряжение на угол p ¤ 2:
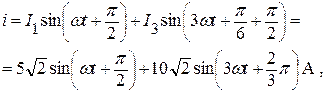
или
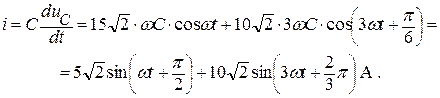
Находим показания амперметра (действующее значение тока электрической цепи):
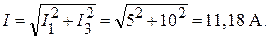
Находим сопротивление участка цепи (RXC) для первой гармоники:
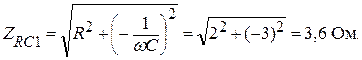
Находим сопротивление участка цепи (RXC) для третьей гармоники:
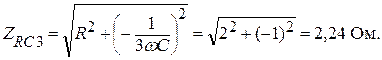
Напряжение участка цепи (RXC) для первой гармоники:
URC1 = ZRC1 I1 = 3,6 × 5 = 18 B.
Напряжение участка цепи (RXC) для третьей гармоники:
URC3 = ZRC3 I3 = 2,24 × 10 = 22,4 B.
Тогда показания вольтметра (действующее значение):
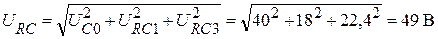 .
.
Мощность цепи:
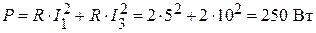 .
.
|
 | |||
| |||
Определить
Показания приборов; мощность и мгновенное значение тока электрической цепи (рис. 4.2.1).
Решение
По действующим значениям напряжений каждой гармоники находим действующее значение напряжения (показания вольтметра):
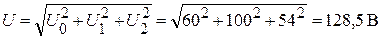 .
.
Вычислим полные сопротивления цепи для каждой гармоники:
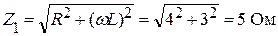 ;
;
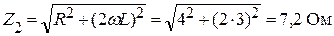 .
.
Найдем действующее значение токов каждой из гармоник:
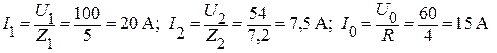 .
.
Находим действующее значение тока I (показания амперметра):
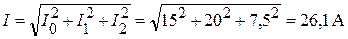 .
.
Мощность цепи определится из суммы мощностей отдельных гармоник:
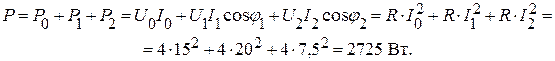
Чтобы записать мгновенное значение тока i необходимо вычислить угол сдвига фаз между током и напряжением соответствующих гармоник:
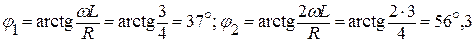 .
.
Тогда мгновенное значение тока электрической цепи рис. 4.2.1 запишется как:
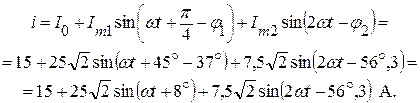
4.3

|
Показания приборов и мощность всей цепи.
Решение
Зная выражение мгновенного значения тока в катушке индуктивности, определим напряжение на катушке для каждой гармоники.
Так как сопротивление катушки индуктивности постоянному току равно нулю, то для нулевой гармоники UL0 = 0.
Для первой гармоники:
ULm1 = XL1 × ILm1 = 5 × 8 = 40 B.
Для второй гармоники:
ULm2 = XL2 × ILm2 = 2wL× ILm2 = 2 × 5 × 6 = 60 B.
Находим мгновенное значение напряжения на катушке индуктивности (оно же и на конденсаторе):
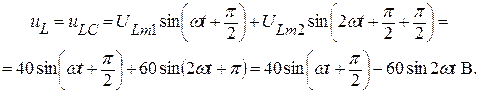
Общее сопротивление участка LC цепи для нулевой гармоники равно нулю, т.к. сопротивление катушки индуктивности постоянному току равно нулю.
Ищем общее сопротивление участка LC цепи для первой и второй гармоник:
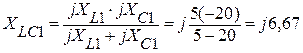 , или модуль комплексного сопротивления
, или модуль комплексного сопротивления 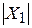 = 6,67 Ом;
= 6,67 Ом; 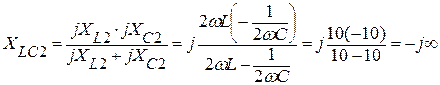 , или модуль комплексного сопротивления
, или модуль комплексного сопротивления 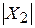 = ¥. Т.е. в контуре LC для второй гармоники имеем резонанс токов.
= ¥. Т.е. в контуре LC для второй гармоники имеем резонанс токов.
Токи цепи для соответствующих гармоник:
I0 = 4 A; 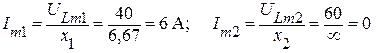 .
.
Мгновенное значение тока всей цепи:
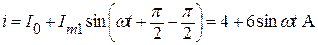 .
.
Действующее значение тока всей цепи (показания амперметра):
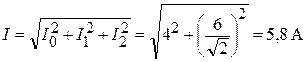 .
.
Сопротивление цепи (для соответствующих гармоник):
R0 = R = 5 Ом; 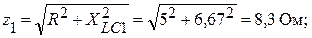
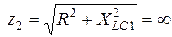 (поскольку XLC2 = ¥).
(поскольку XLC2 = ¥).
Напряжение цепи (для соответствующих гармоник):
U0 = R0 I0 =5 × 4 = 20 B; Um1 = z1I m1 = 8,3 × 6 = 49,8 B; Um2 = 60 B.
Так как ток цепи второй гармоники равен нулю (Im2 = 0), то для второй гармоники тока не создается падение напряжения на активном сопротивлении, т.е. (UR2 = 0) и тогда:
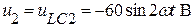 .
.
Ищем мгновенное значение напряжения всей цепи:
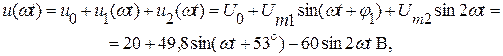
где 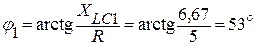 .
.
Находим действующее значение напряжения всей цепи (показания вольтметра):
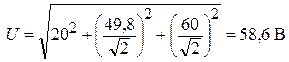 .
.
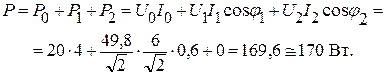
или
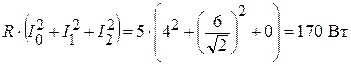 .
.
Дата добавления: 2015-12-11; просмотров: 975;

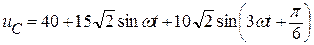 В;
R = 2 Ом; XL = 1 Ом; XC = 3 Ом.
В;
R = 2 Ом; XL = 1 Ом; XC = 3 Ом.
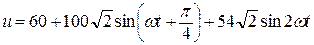 .
.