Резонансные явления в электрических цепях
2.1
|
|
|
Дано
 |  |
|
 R = 10,6 Ом; L = 2,26×10-3 Гн; E = 50×10-6 B;
R = 10,6 Ом; L = 2,26×10-3 Гн; E = 50×10-6 B;
l = 2000 м (длина электромагнитной волны)
|
 рис. 2.1.1.
рис. 2.1.1.
Определить
Емкость конденсатора, при которой контур настроен в резонанс. Рассчитать добротность контура и напряжение на катушке индуктивности.
Решение
Частоту источника найдем из соотношения:
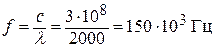 ,
,
где с - скорость распространения электромагнитных волн (скорость света).
Тогда
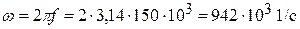 .
.
Откуда
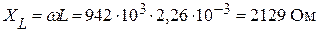 .
.
При резонансе в последовательной R,L,C цепи XL = XC и следовательно:
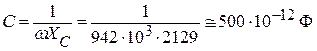 .
.
Тогда резонансная частота:
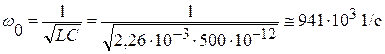 .
.
Вычислим добротность контура:
 .
.
Вычислим напряжение на катушке индуктивности:
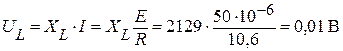 .
.
2.2
 | |||
| |||
Решение
Поскольку контур настроен в резонанс, то ток I3 будет совпадать по фазе с напряжением U, а ток I1 будет отставать от напряжения 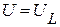 на угол
на угол 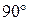 . С учетом этого построим векторную диаграмму рис. 2.2.2.
. С учетом этого построим векторную диаграмму рис. 2.2.2.

Так как I1 = I3 (по условию), то
I1 = I3 = 10 A.
Находим индуктивное сопротивление катушки:
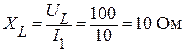 .
.
С другой стороны
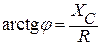 ,
,
но j = 45о и, следовательно:
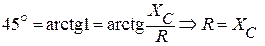 .
.
Но
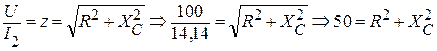 .
.
Так как 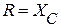 , то
, то
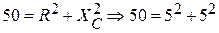 .
.
Откуда
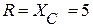 Ом.
Ом.
Электрические цепи, содержащие магнитные связи
3.1

Решение
Найдем напряжение 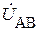 между точками А и В:
между точками А и В:
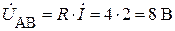 .
.
С другой стороны:
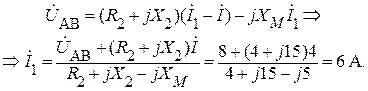
Тогда
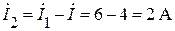 .
.
Найдем напряжение 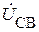 между точками С и В:
между точками С и В:
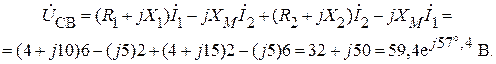
Таким образом, показания вольтметра: UV = 59,4 B.
Активная мощность цепи:
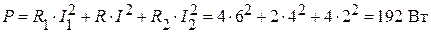 .
.
или
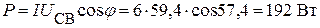 .
.
Таким образом, показания ваттметра: PW = 192 Bт.
Реактивная мощность цепи:
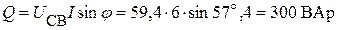 .
.
или
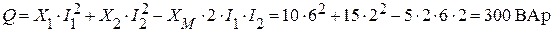 .
.
Комплексная мощность цепи:
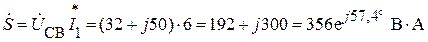 .
.
3.2
 | |||
| |||
Решение
В контурных токах система уравнений для электрической цепи
рис. 3.2.1 в матричной форме будет иметь вид:
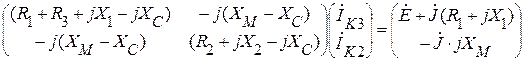 .
.
Раскрытие главного определителя системы дает:
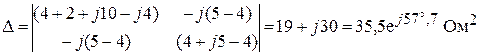 .
.
Произведя замену первого столбца в матрице коэффициентов, столбцовой матрицей свободных параметров получим:
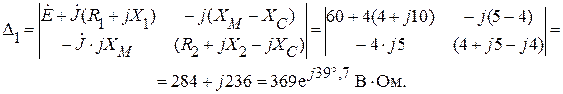
Откуда
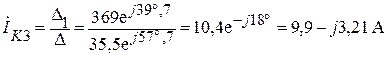 .
.
Произведя аналогичную замену для второго столбца в матрице коэффициентов, будем иметь:
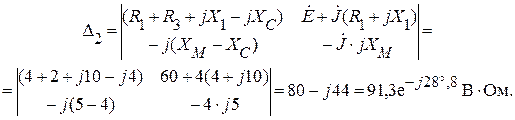
Тогда
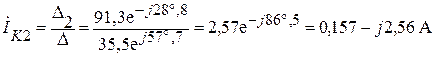 .
.
Находим токи 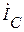 и
и 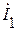 :
:
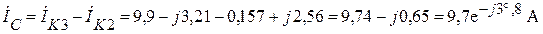 ;
;
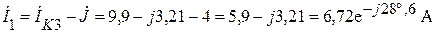 .
.
Ищем напряжение между точками А и В:
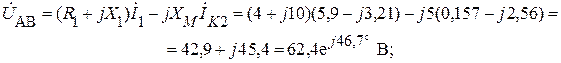
или
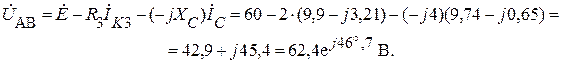
Ищем напряжение между точками В и С:
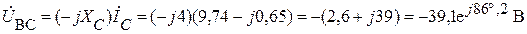 .
.
или
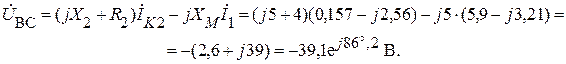
Проверяем баланс мощностей.
Активная мощность цепи:
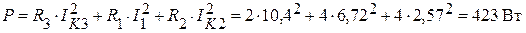 .
.
Реактивная мощность цепи:
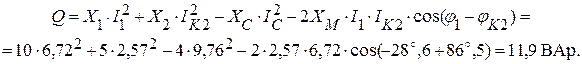
Комплексная мощность цепи:
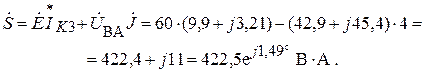
Расхождения в вычислениях незначительны.
|
|

Определить
Параметры трансформатора R1, R2, XL1, XL2 и XM (рис. 3.3.1). Построить векторную диаграмму.
Решение
Режим холостого хода (ключ K разомкнут).
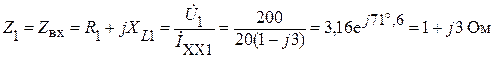 .
.
Таким образом, активное и реактивное сопротивления первичного контура соответственно равны: R1 = 1 Ом; ХL1 = 3 Ом.
Комплексное сопротивление взаимной индукции:
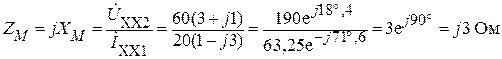 ,
,
или XM = 3 Ом.
Режим короткого замыкания (ключ К замкнут).
Для первичного и вторичного контуров, составим следующую систему уравнений:
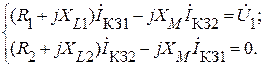
Из первого уравнения системы находим ток IКЗ2:
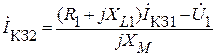 .
.
Подставив полученный результат во второе уравнение, запишем:
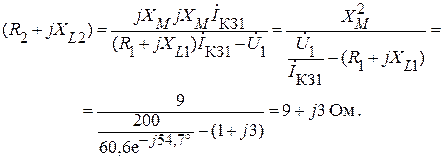
Таким образом, активное и реактивное сопротивления вторичного контура соответственно равны: R2 = 9 Ом; ХL2 = 3 Ом.
Векторную диаграмму (рис. 3.3.2) начинаем строить по уравнению для вторичной цепи. В соответствующем масштабе отложим вектор тока IКЗ2. Вектор IКЗ2R2будет совпадать (по направлению) с вектором IКЗ2. Вектор IКЗ2 jXL2 опережает вектор тока IКЗ2 на 90о. Вектор I1КЗ jXМ, с учетом знака, будет замыкающим и направлен в начало координат. По вектору IКЗ1 jXМ находим направление вектора тока первичной цепи IКЗ1, который опережает вектор IКЗ1 jXМ на 90о. Дальнейшее построение векторов первичной цепи в пояснениях не нуждается.

3.4
|

Определить
Параметр XС, при котором мощность выделяемая источником будет чисто активная, вычислить эту мощность. Параметр XС, при котором мощность развиваемая источником равна нулю.
Решение
Составим систему уравнений для левого и правого контуров электрической цепи:
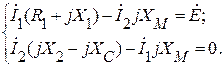
Мощность, развиваемая источником, будет чисто активная в режиме резонанса, когда индуктивные и взаимоиндуктивная составляющие компенсируются емкостной составляющей.
Из первого уравнения системы находим ток 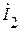 :
:
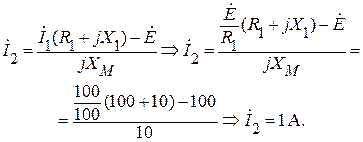
Величину емкостного сопротивления XС найдем из второго уравнения системы.
Так как 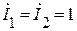 А, то
А, то
XС = X2 – XM = 20 – 10 = 10 Ом.
Активная мощность:
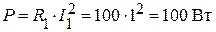 ,
,
или 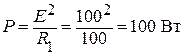 .
.
Из второго уравнения системы найдем величину XС для случая, когда мощность, развиваемая источником, равна нулю. Это означает, что ток I1 = 0, тогда получим:
(X2 – XС) I2 = 0 Þ X2 – XС = 0 Þ X2 = XС = 20 Ом.
Дата добавления: 2015-12-11; просмотров: 797;

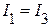 , ток
, ток 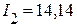 А;
А;
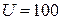 В.
Определить
Токи
В.
Определить
Токи 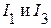 , а так же параметры элементов схемы рис. 2.2.1.
, а так же параметры элементов схемы рис. 2.2.1.
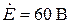 ;
; 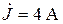 ; R1 = R2 = 4 Ом;
R3 = 2 Ом; X1 =10 Ом; X2 = 5 Ом;
XC = 4 Ом; XМ = 5 Ом.
Определить
Все токи и напряжения между узлами А,В и В,С (рис. 3.2.1). Проверить баланс мощностей.
; R1 = R2 = 4 Ом;
R3 = 2 Ом; X1 =10 Ом; X2 = 5 Ом;
XC = 4 Ом; XМ = 5 Ом.
Определить
Все токи и напряжения между узлами А,В и В,С (рис. 3.2.1). Проверить баланс мощностей.