Энергия магнитного поля двух индуктивно связанных катушек
Рассмотрим две ветви содержащие индуктивно связанные катушки.

Энергию поля токов 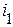 и
и 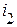 двух индуктивно связанных ветвей будем определять из энергии, которая получена от действия источников питания этих ветвей
двух индуктивно связанных ветвей будем определять из энергии, которая получена от действия источников питания этих ветвей 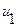 и
и 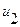 . При этом будем полагать, что вначале
. При этом будем полагать, что вначале 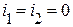 , т.е. обе ветви разомкнуты.
, т.е. обе ветви разомкнуты.
Пусть сначала источник питания включен только в первую ветвь, содержащую индуктивность  , а вторая ветвь с индуктивностью
, а вторая ветвь с индуктивностью 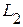 остается разомкнутой, т.е.
остается разомкнутой, т.е. 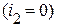 . Тогда при возрастании тока от нуля до значения
. Тогда при возрастании тока от нуля до значения 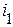 за промежуток времени
за промежуток времени  этот источник питания должен отдать энергию:
этот источник питания должен отдать энергию:
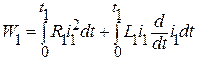 .
.
Если вычисть из энергии  энергию, которая рассеивается в сопротивлении
энергию, которая рассеивается в сопротивлении  (первое слагаемое в правой части уравнения), то окажется, что источник питания включенный в первую ветвь, отдаст магнитному полю энергию:
(первое слагаемое в правой части уравнения), то окажется, что источник питания включенный в первую ветвь, отдаст магнитному полю энергию:
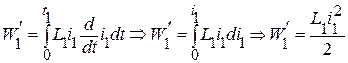 .
.
Пусть в момент времени  другой источник включается во вторую ветвь с индуктивностью
другой источник включается во вторую ветвь с индуктивностью 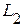 и к моменту времени
и к моменту времени 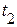 ток в этой ветви возрастает от нуля до значения
ток в этой ветви возрастает от нуля до значения 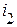 . Если за этот промежуток времени ток
. Если за этот промежуток времени ток 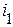 в первой ветви остается постоянным, то источник питания второй ветви, по аналогии, должен отдать магнитному полю энергию
в первой ветви остается постоянным, то источник питания второй ветви, по аналогии, должен отдать магнитному полю энергию
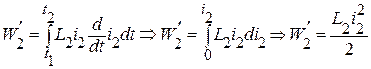 .
.
Однако при нарастании тока 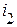 в первой ветви будет наведена ЭДС
в первой ветви будет наведена ЭДС 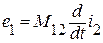 . В этом случае, чтобы ток в первой ветви остался постоянным (
. В этом случае, чтобы ток в первой ветви остался постоянным ( 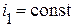 ), первый источник должен создать напряжение
), первый источник должен создать напряжение 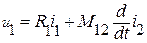 , необходимое не только для уравновешивания падения напряжения
, необходимое не только для уравновешивания падения напряжения 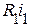 , но и наводимую в первой ветви ЭДС
, но и наводимую в первой ветви ЭДС 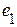 . Поэтому энергия, отдаваемая первым источником магнитному полю за время нарастания тока
. Поэтому энергия, отдаваемая первым источником магнитному полю за время нарастания тока 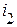 , запишется в виде:
, запишется в виде:

В итоге полную энергию магнитного поля при токах 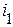 и
и 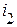 в двух индуктивно связанных ветвях определит выражение:
в двух индуктивно связанных ветвях определит выражение:
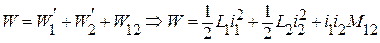 .
.
Если сначала источник питания включить во вторую ветвь, а затем включить источник питания в первой ветви и повторить аналогичный ход рассуждений, то в конечном итоге можем записать:
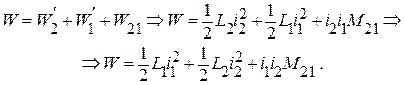
Разница в полученных выражениях заключается лишь в том, что в первом случае выражение содержит коэффициент взаимной индукции 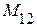 , равный потокосцеплению первого элемента при постоянном токе во втором, а в другом случае выражение содержит коэффициент взаимной индукции
, равный потокосцеплению первого элемента при постоянном токе во втором, а в другом случае выражение содержит коэффициент взаимной индукции 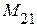 , равный потокосцеплению второго элемента при постоянном токе в первом. При этом, конечное состояние цепи в обоих случаях одинаково. Поэтому можно сделать заключение о равенстве взаимных индуктивностей:
, равный потокосцеплению второго элемента при постоянном токе в первом. При этом, конечное состояние цепи в обоих случаях одинаково. Поэтому можно сделать заключение о равенстве взаимных индуктивностей: 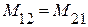 .
.
Дата добавления: 2015-12-11; просмотров: 1684;
