Резонансная характеристика
Покажем зависимости напряжений на элементах контура от частоты при поддержании на зажимах цепи постоянного напряжения.
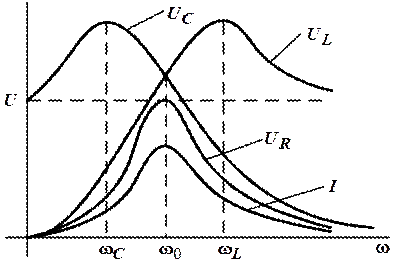
Здесь имеет место симметрия максимумов кривых напряжения на реактивных элементах:  .
.
Падение напряжения на индуктивности:  .
.
Падение напряжения на емкости: 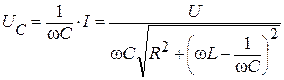 .
.
Преобразование полного сопротивления цепи дает:
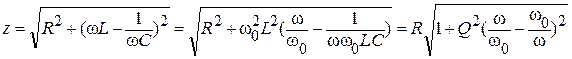 .
.
Тогда действующее значение тока при резонансе:
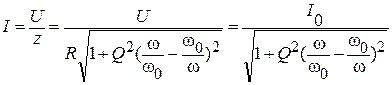 ,
,
где 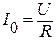 - действующее значение тока при резонансе.
- действующее значение тока при резонансе.
Из последнего выражения следует, что влияние параметров на вид резонансной кривой полностью учитывается добротностью Q контура, причем, чем выше добротность резонансного контура, тем лучше избирательные свойства цепи (за счет узости относительной ширины полосы пропускания контура).
Это свойство резонансных колебательных контуров используется для выделения сигнала данной частоты из совокупности различных частот и широко применяется в электросвязи и радиотехники. При этом режим резонанса является нормальным рабочим режимом.
Резонанс токов
Рассмотрим цепь, состоящую из параллельно включенных активного, индуктивного и емкостного сопротивлений.

| Для этой цепи комплексная проводимость:
 , , 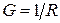 - активная проводимость. Угол сдвига фаз: - активная проводимость. Угол сдвига фаз:
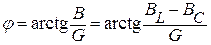 .
Полная проводимость цепи: .
Полная проводимость цепи: 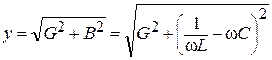 . .
|
Из этого выражения видно, что взаимная компенсация реактивных проводимостей достигается при условии когда 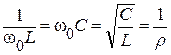 , т.е. когда
, т.е. когда 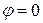 ;
; 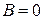 .
.
Тогда полная проводимость цепи 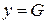 , при этом в цепи наблюдается резонанс.
, при этом в цепи наблюдается резонанс.
Векторная диаграмма при резонансе имеет вид:

| Здесь вектор тока I всей цепи совпадает с вектором тока IG в активной проводимости, поскольку токи IL и IC находятся в противофазе. При частотах близких к резонансным токи в параллельных ветвях содержащих реактивные элементы могут значительно превышать ток на входе. Поэтому резонанс при параллельном соединении называют резонансом токов. |
Для идеального резонансного контура, когда входное сопротивление цепи бесконечно велико, или когда активная проводимость G = 0, имеет место равенство: 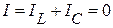 .
.
Кратность превышения токов в ветвях с реактивными элементами получают из соотношений:
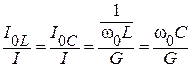 ,
,
где 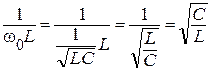 . Аналогично для
. Аналогично для 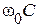 .
.
Таким образом, отношение 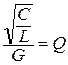 есть добротность контура при параллельном соединении элементов
есть добротность контура при параллельном соединении элементов 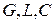 .
.
Дата добавления: 2015-12-11; просмотров: 2624;
