Резонанс в сложных цепях
Условия резонанса для разветвленной цепи с несколькими индуктивными и емкостными элементами дают для угловой частоты 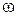 уравнения, которые могут иметь несколько вещественных корней. Это означает, что у разветвленной цепи может быть несколько резонансных частот. В качестве примера рассмотрим электрическую цепь, потерями в которой можно пренебречь.
уравнения, которые могут иметь несколько вещественных корней. Это означает, что у разветвленной цепи может быть несколько резонансных частот. В качестве примера рассмотрим электрическую цепь, потерями в которой можно пренебречь.

Входное сопротивление для приведенной цепи будет чисто реактивным и запишется в виде:
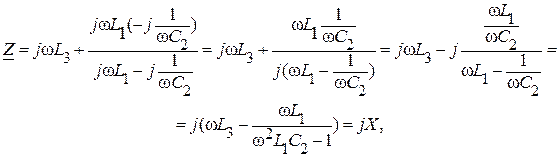
где X - реактивное сопротивление цепи.
Так как в данном случае активными сопротивлениями цепи пренебрегаем, то резонанс наступит при В = 0 или при Х = 0, причем, если Х = 0, то В = ∞, и наоборот, если В = 0, то Х = ∞.
В рассматриваемом случае реактивное сопротивление Х будет равно бесконечности (Х = ∞) при 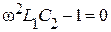 или
или 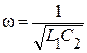 . На этой частоте наступает резонанс токов в параллельных ветвях с элементами
. На этой частоте наступает резонанс токов в параллельных ветвях с элементами  и
и 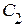 , т.е.
, т.е. 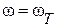 .
.
Полагая реактивное сопротивление Х равное нулю (Х = 0), можем записать:
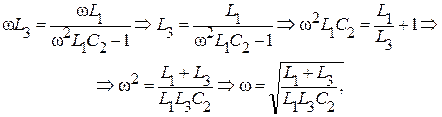
т.е. 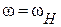 .
.
На этой частоте наступает резонанс напряжений в последовательном контуре. Таким образом, у рассмотренной цепи имеем две резонансные частоты: 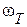 и
и 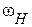 .
.
Покажем частотные характеристики проводимостей и сопротивлений рассмотренной цепи.

На приведенном рисунке кривые 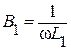 и
и 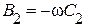 представляют характеристики проводимостей двух параллельных ветвей 1 и 2. Суммируя ординаты этих кривых, получим характеристику эквивалентной проводимости
представляют характеристики проводимостей двух параллельных ветвей 1 и 2. Суммируя ординаты этих кривых, получим характеристику эквивалентной проводимости 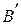 ветвей 1 и 2. Кривая
ветвей 1 и 2. Кривая 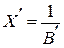 представляет собой эквивалентное сопротивление этих же параллельных ветвей. Тогда, суммируя ординаты кривых
представляет собой эквивалентное сопротивление этих же параллельных ветвей. Тогда, суммируя ординаты кривых 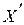 и
и 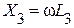 , строим характеристику входного сопротивления цепи X. Эта характеристика имеет две особые точки при
, строим характеристику входного сопротивления цепи X. Эта характеристика имеет две особые точки при 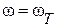 и
и 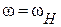 .
.
Дата добавления: 2015-12-11; просмотров: 1039;
