Метод контурных токов
При расчете сложной электрической цепи можно ограничиться совместным решением уравнений составленных по второму закону Кирхгофа для токов, замыкающихся по независимым контурам схемы, число которых определяют из выражения 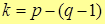 . Направление контурного тока следует выбирать по направлению тока в ветви, входящей только в этот контур.
. Направление контурного тока следует выбирать по направлению тока в ветви, входящей только в этот контур.
При составлении уравнений следует пользоваться следующими правилами:
1. В левой части уравнений записывают алгебраическую сумму всех падений напряжения на элементах (резисторах), от протекания по ним контурного тока, а также падения напряжения на тех элементах, через которые протекают контурные токи смежных контуров. Причем, эти падения напряжения записывают со знаком плюс, если направления смежных контурных токов совпадает с контурным током рассматриваемого контура и со знаком минус – если не совпадает.
В правой части уравнений записывают все ЭДС, входящие в рассматриваемый контур со знаком плюс, если их направление совпадает с направлением контурного тока и со знаком минус, если не совпадает.
Если схема содержит источники тока, то токи источников образуют свои замкнутые контуры связи, причем в эти контуры не должны входить ветви, по которым выбраны направления других контурных токов. Если вызванные током источника падения напряжения на элементах совпадают с контурным током, то в правой части уравнений они записываются со знаком минус, если не совпадает – со знаком плюс.
Рассмотрим электрическую цепь, содержащую источники ЭДС и тока. Требуется найти токи во всех ветвях.
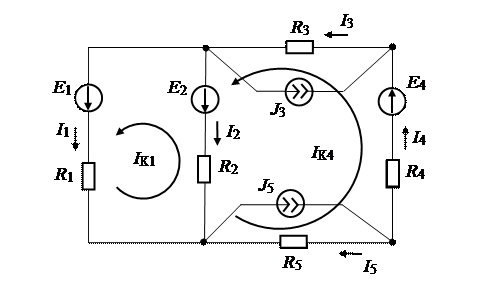
Для приведенной схемы 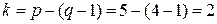 , т.е. необходимо составить систему из двух уравнений. Направление контурного тока IK1 выбираем по направлению тока I1 первой ветви, а контурного тока IK4 выбираем по направлению тока I4 четвертой ветви.
, т.е. необходимо составить систему из двух уравнений. Направление контурного тока IK1 выбираем по направлению тока I1 первой ветви, а контурного тока IK4 выбираем по направлению тока I4 четвертой ветви.
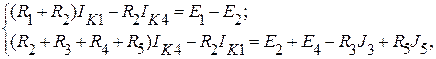
где
IK1 = I1 и IK4 = I4.
Тогда
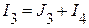 ;
; 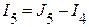 ;
; 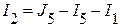 или
или 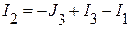 .
.
Если направление контурного тока выберем по направлению тока, например, в третьей ветви IK3 = I3, то система уравнений примет вид:
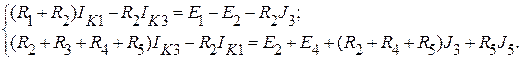
Или в матричной форме:
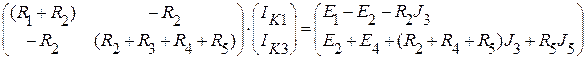 .
.
Схему с источниками тока можно упростить (за счет уменьшения числа ветвей и узлов), выполнив преобразования источников тока в источники ЭДС.
В этом случае электрическая цепь примет вид:
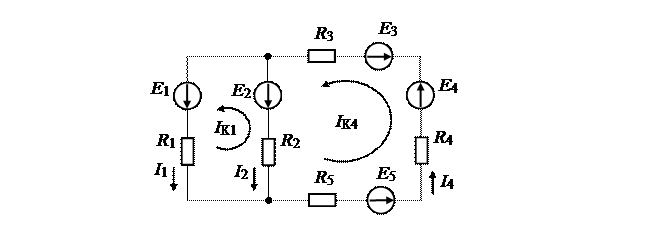
Для данной схемы: 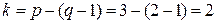 , т.е. как и в первом случае необходимо составить систему из двух уравнений.
, т.е. как и в первом случае необходимо составить систему из двух уравнений.
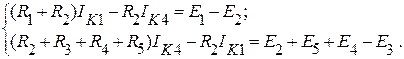
Здесь 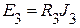 ;
; 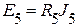 .
.
Дата добавления: 2015-12-11; просмотров: 844;
