Теорема (метод) компенсации
Метод основан на принципе компенсации, когда по схеме приращений определяют приращение тока в цепи вследствие изменения сопротивления ветви. Схема приращений образуется исключением источников энергии в исходной схеме и включением в ветвь последовательно с новым сопротивлением источника напряжения.
1. Ток цепи не изменится, если в ней сопротивление пассивного элемента заменить источником ЭДС, величина которого равна напряжению на этом элементе, и направлена навстречу току в этом элементе (E = R∙I).
2. Изменение тока ветви на величину ∆I при изменении сопротивления на величину ∆R будет таким же, если вместо ∆R включить ЭДС (E = ∆R∙I), направленную встречно первоначальному току в этой ветви.
Рассмотрим электрическую цепь, в ветви которой надо определить приращение тока при изменении в этой ветви сопротивления.
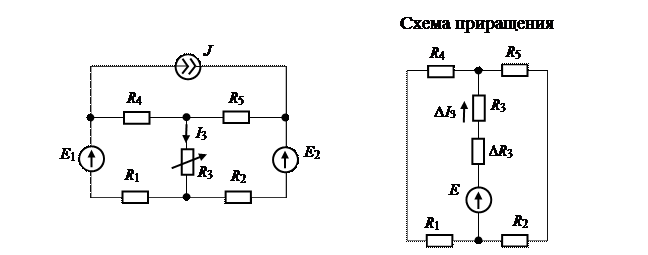
Согласно схеме приращения находим приращение тока ∆I3:
,
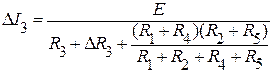где Е = ∆R3I3.
Метод компенсации часто применяют при определении чувствительности схемы к изменению ее параметров.
Метод эквивалентного источника напряжения
(теорема Гельмгольца-Тевенена)
Метод основан на теореме об эквивалентном источнике, когда активный двухполюсник по отношению к рассматриваемой ветви может быть заменен эквивалентным источником напряжения, ЭДС которого равна напряжению холостого хода на зажимах этой ветви, а его внутреннее сопротивление равно входному сопротивлению двухполюсника.
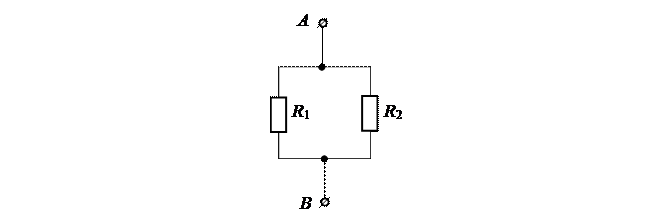
Рассмотрим электрическую цепь.
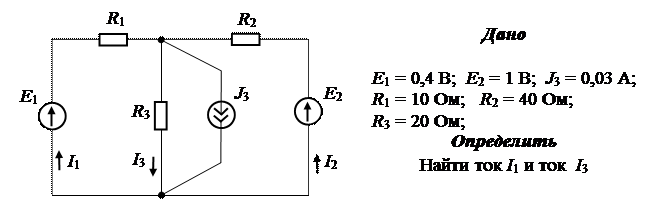
Решение
Ищем ток I1.
Представим исходную схему в следующем виде:
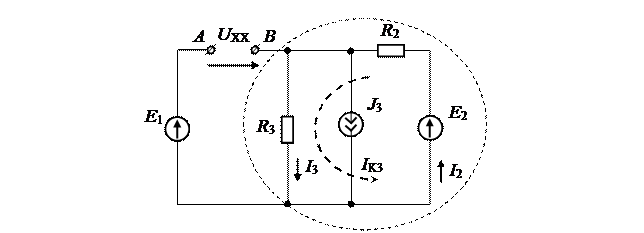
Для выделенной структуры составим уравнение по методу контурных токов и найдем ток I3:
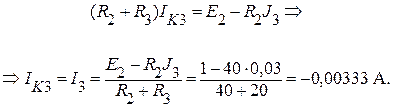
Теперь можем найти напряжение холостого хода между зажимами А и В:
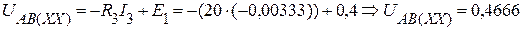В.
Входное сопротивление к зажимам А, В найдем согласно схеме:
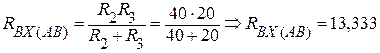Ом.
Находим ток I1:
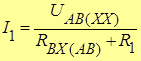
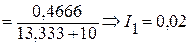A.
Ищем ток I3.
Представим исходную схему в виде:
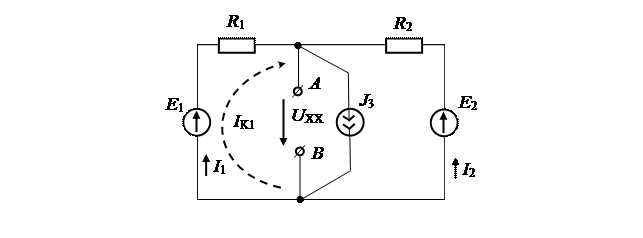
Для данной схемы уравнение по методу контурных токов будет иметь вид:
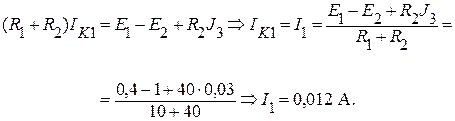
Тогда
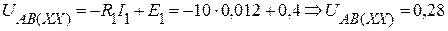В.
Входное сопротивление к зажимам А, В найдем согласно схеме:
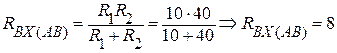Ом.
Находим ток I3:
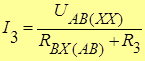
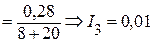А.
Рассмотрим электрическую цепь, в которой активный двухполюсник подключен к ветви с последовательно включенными сопротивлениями и амперметром.
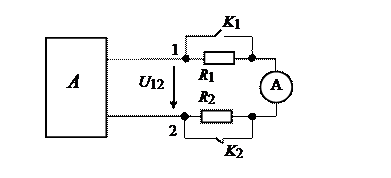
Из опыта известны два показания амперметра: тока IA1, когда оба ключа разомкнуты и тока IA2, когда ключ K1 замкнут, а ключ K2 разомкнут.
Требуется вычислить показания амперметра при разомкнутом ключе K1 и замкнутом ключе K2 (см. рисунок).
Составляем уравнения для всех трех режимов:
1. 
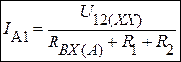; 2. 
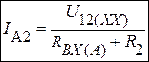; 3.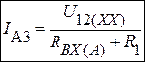 
,
где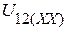 
- напряжение холостого хода на зажимах исследуемой ветви.
Тогда из первого уравнения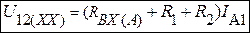 
.
Из второго уравнения находим входное сопротивление двухполюсника.
;
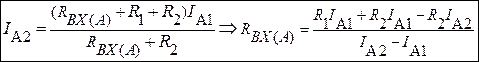После чего находим ток IА3.
Дата добавления: 2015-12-11; просмотров: 609;