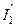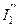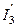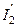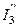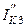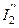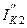Если ветвь содержит источник тока, и он направлен к узлу, то в правой части уравнения его учитывают со знаком плюс.
Рассмотрим принцип составления уравнений методом узловых напряжений.
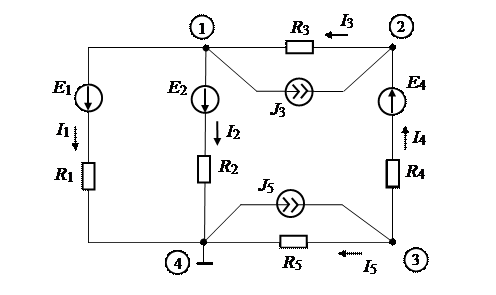
Для данной схемы необходимо составить систему из трех уравнений для узлов 1,2,3. Потенциал четвертого узла равен нулю. Тогда с учетом сформулированных правил получим:
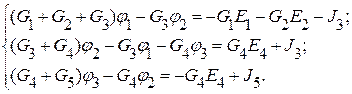
Здесь G1= 1/R1; G2= 1/R2; G3= 1/R3; G4= 1/R4; G5= 1/R5.
После нахождения потенциалов, ищем токи в ветвях, предварительно указав на схеме выбранные направления токов.
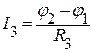 ;
; 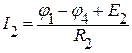 ;
; 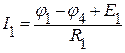 ;
; 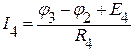 ;
;
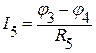 .
.
Метод наложения
При действии нескольких источников напряжения и токов в линейной электрической цепи неизвестные токи в ветвях такой цепи можно найти суммированием токов от каждого источника в отдельности. При этом, исключенные из схемы источники заменяют их внутренними сопротивлениями, закоротив источники ЭДС и разомкнув источники тока. Рассмотрим электрическую цепь. Пользуясь методом наложения, определим токи в ветвях схемы.
Исключив из схемы источник тока J2 , найдем частичные токи в ветвях под воздействием источника ЭДС E1.
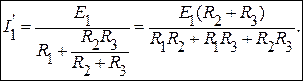
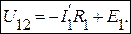
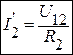 ;
; 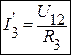 . Или
. Или 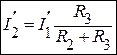 ;
; 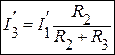 .
.
Исключим из схемы источник E1 и найдем частичные токи в ветвях от воздействия источника тока J2.
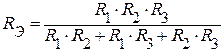 .
. 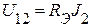 .
.
Ищем токи в ветвях: 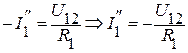 ;
; 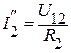 ;
; 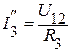 .
.
Эти токи можно найти из системы уравнений: 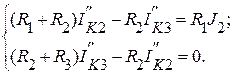
Истинные значения токов в ветвях найдем из соответствующих сумм частных токов:
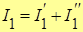 ;
; 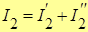 ;
; 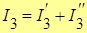 .
.
Рассмотренный метод, однако, не применим при вычислении мощностей, так как мощность есть квадратичная функция тока или напряжения.
Дата добавления: 2015-12-11; просмотров: 900;

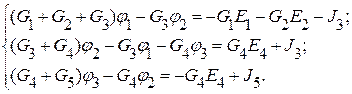
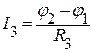 ;
; 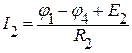 ;
; 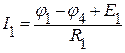 ;
; 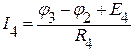 ;
;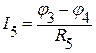 .
.



































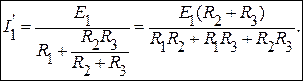
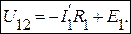
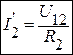 ;
; 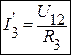 . Или
. Или 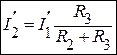 ;
; 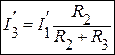 .
.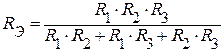 .
. 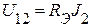 .
.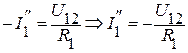 ;
; 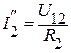 ;
; 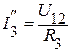 .
.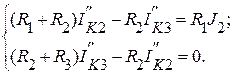
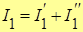 ;
; 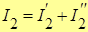 ;
; 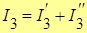 .
.