Коэффициент бетта и характерная линия

В условиях рыночного равновесия цены финансовых активов и ожидаемые ставки доходности от инвестирования в них формируются таким

образом, что хорошо осведомленные инвесторы удовлетворены составом своих оптимальных портфелей. Исходя из того что ожидаемая ставка доходности должна компенсировать инвесторам риск их вложений, мы определяем риск, присущий ценной бумаге в соответствии с величиной ее ожидаемой доходности в условиях равновесия. Таким образом, риск ценной бумаги А оказывается выше, чем риск, присущий ценной бумаге В, если в условиях равновесия ожидаемая доходность А превосходит ожидаемую доходность В. Если внимательно рассмотреть приведенный на рис.1 график рынка капиталов, мы увидим, что для оптимальных (эффективных) портфелей характерна следующая зависимость: чем больше стандартное отклонение их доходности, тем больше ожидаемая доходность Е{г) и, следовательно, тем выше риск. Таким образом, риск эффективного портфеля определяется величиной а. Однако стандартное отклонение доходности не позволяет в рамках ЦМРК измерить риск ценной бумаги. Общая мера присущего ценной бумаге риска или, говоря иначе, систематического риска, задается коэффициентом "бета". С формальной точки зрения коэффициент "бета" показывает предельный вклад доходности данной ценной бумаги в дисперсию доходности рыночного портфеля.

В соответствии с ЦМРК в состоянии равновесия премия за риск любой

ценной бумаги равна соответствующему значению "бета", умноженному на премию за риск всего рыночного портфеля. Эта взаимосвязь описывается следующим математическим выражением:

E (rj) – rf = bj [E (rm) - rf]

Данное выражение описывает так называемую линию доходности рынка ценных бумаг, или ЛДРЦБ (security market line, SML), приведенную на рис. 1. Обратите внимание, что на рис.1 соответствующее значение "бета" ценной бумаги откладывается по горизонтальной оси, а величина ожидаемой доходности — по вертикальной. Наклон линии доходности рынка ценных бумаг соответствует премии за риск рыночного портфеля. В приведенном примере рыночная премия за риск составляет 0,08, или 8% годовых, и соотношение для ЛДРЦБ принимает вид:

E (rj) – rf= 0,08bj

Коэффициент b дает также возможность измерить относительную меру чувствительности фактической доходности данной ценной бумаги по отношению к фактической доходности всего рыночного портфеля. Таким образом, если фактическая доходность рыночного портфеля оказывается на У%, меньше (или больше) ожидаемой, то полученная доходность ценной бумаги j будет равняться значению, которое больше (или меньше) ожидаемого на величину, равную b, х У%. В связи с этим ценные бумаги, имеющие высокий коэффициент "бета" (превышающий 1) называются "агрессивными", поскольку их доходность обладает более сильной динамикой, чем Доходность всего рыночного портфеля. Другими словами, их доходность сильнее повышается при общем подъеме на рынке и, соответственно, сильнее снижается при спаде. Аналогично этому ценные бумаги, коэффициенты "бета" для которых невелики (менее 1), называются "оборонительными". Рыночный портфель имеет по определению значение "бета", равное 1, а ценные бумаги с "бета", равным 1, называются "среднерисковыми".

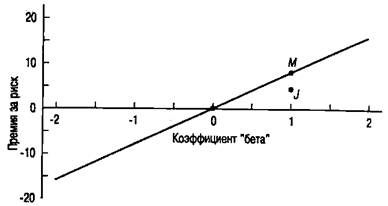
Рис. 1. Линия доходности рынка ценных бумаг

Примечание. Все ценные бумаги (а не только те из них, которые входят в эффективные портфели) расположены на ЛДРЦБ при условии, что они правильно оцениваются в соответствии с ЦМРК.

Если же какая-либо ценная бумага характеризуется ожидаемой доходностью и коэффициентом "бета", не принадлежащими линии доходности рынка ценных бумаг, то »то противоречит ЦМРК. В частности, представьте себе некоторую ценную бумагу, для которой ожидаемая доходность и значение "бета" представлены точкой, показанной на рис.2. Поскольку эта точка располагается ниже линии доходности рынка ценных бумаг, ее ожидаемая доходность оказывается "слишком низкой", чтобы уравновесить спрос и предложение. (Или мы можем сказать, что в данном случае рыночная цена слишком высока.)

Такая ситуация входит в противоречие с ЦМРК, поскольку это означает, что либо рынок не находится в состоянии равновесия, либо инвесторы не пришли к согласию по вопросу о распределении ставок доходности для обращающихся на рынке ценных бумаг, или же инвесторы не заняты поиском оптимальных инвестиционных решений.

Коэффициент "бета" любого индивидуального инвестиционного портфеля, лежащего на линии доходности рынка ценных бумаг (т.е. любого портфеля, сформированного в результате объединения рыночного портфеля и безрисковых активов) равняет я значению той его части, которая вложена в рыночный портфель. Например, "бета ля инвестиционного портфеля, в котором 0,75 вложено в рыночный портфель, а,25 — в безрисковые активы, равна 0,75.

Избыточная доходность рыночного портфеля по сравнению с инвестициями в абсолютно надежные ценные бумаги равна rm - rf. Избыточная доходность инвестиций в ценные бумаги типа i по сравнению со средним уровнем равна ri - rf. Если избыточную доходность ценной бумаги i отложить по одной оси, а избыточную среднерыночную доходность — по другой, то получим график характеристик ценной бумаги (рис.2). Такой график можно начертить для любой ценной бумаги или любого портфеля ценных бумаг. Угол наклона прямой равен b i, - коэффициенту ценной бумаги i, а отрезок, отсекаемый линией на вертикальной оси, равен a i.

Коэффициент a ценной бумаги - это избыточная доходность ценной бумаги по сравнению с доходностью ценной бумаги, свободной от риска, в случае, когда доходность рыночного портфеля равна доходности по ценным бумагам, свободным от риска (т.е. избыточная доходность на рынке нулевая). Когда избыточная доходность на рынке равна 0, мы вправе ожидать, что каждая ценная бумага в состоянии рыночного равновесия также будет иметь нулевую избыточную доходность (a = 0). В то время как средневзвешенная (a -коэффициентов всех ценных бумаг равна 0, a некоторых ценных бумаг положительна, а некоторых — отрицательна, в зависимости от фактически наблюдаемой ставки доходности.

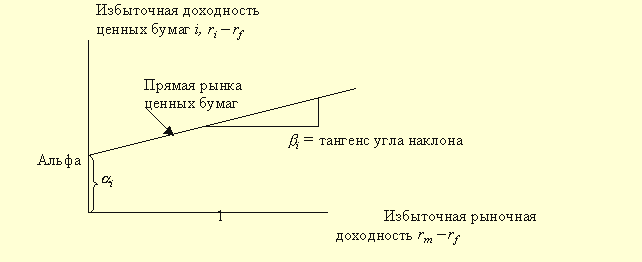
Рис.2. Линия характеристик ценной бумаги

Если рынок считает, что те условия, которые привели к тому, что а оказалась положительной, в будущем сохранятся, то ценная бумага становится привлекательной. Ее будут покупать и цена её вырастет, а доходность упадет, так что ожидаемый коэффициент a окажется равным 0. Так как рынок несовершенен (да и прогнозы не идеальны), не удивительно, что когда через некоторое время начинают чертить график фактической доходности, оказывается, что a -коэффициент ценной бумаги не равен в точности 0. Если мы считаем, что рынок находится в состоянии равновесия, то наиболее вероятная оценка уровня a -коэффициента ценной бумаги равна 0, но если фактическая a , вычисленная на основе графика избыточной доходности, будет равна 0, то это окажется большим сюрпризом.

Поскольку САРМ пренебрегает важными факторами, которые инвесторы на практике принимают во внимание, можно ожидать, что в результате воздействия этих неучтенных факторов a -коэффициенты всех ценных бумаг (или классы ценных бумаг) будут либо положительными, либо отрицательными. Например, обыкновенные акции энергетической компании, строящей АЭС, могут иметь отрицательный a -коэффициент, так как САРМ не учитывает особые виды риска, связанные со строительством АЭС, а рынок обязательно примет их во внимание.

Иногда считают, что коэффициент b подходит для измерения риска акции. Коэффициент сравнивает корреляцию рыночной доходности и доходности конкретной акции (r i , m), среднеквадратическое отклонение акции (s i) со среднеквадратическим отклонением рыночного портфеля (s m). b коэффициент портфеля равен средневзвешенной b -коэффициентов его компонентов:

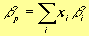
29. Оценка облигаций: кривая доходности и форвардные ставки

Теория чистых ожиданий и теория предпочтения ликвидности в качестве главного элемента рассматривают форвардные ставки. В соответствии с теорией чистых ожиданий сегодняшняя форвардная ставка в среднем равна ожидаемой будущей ставке спот для того же периода, для которого рассчитана форвардная ставка. Теория полагает: на рынке присутствует большое число инвесторов, стремящихся получить наибольший уровень доходности и не имеющих предпочтений относительно выбора облигаций с каким-то определенным временем до погашения в рамках некоторого инвестиционного горизонта. Поэтому рост доходности облигации с каким-либо сроком погашения по сравнению с другими облигациями привлечет к ним внимание инвесторов. В результате активной покупки данных облигаций цена их возрастет, и, следовательно, понизится доходность. Поскольку вкладчики одновременно будут продавать другие облигации, чтобы купить более доходные, то цена их упадет, а доходность вырастет. В результате таких действий через некоторое время на рынке установится равновесие. Инвестор будет безразличен, какую облигацию купить, поскольку любая стратегия в такой ситуации принесет ему одинаковую доходность. Если произойдет отклонение в доходности бумаг от состояния равновесия, то вновь начнется активная торговля и через некоторое время равновесие восстановится. Таким образом, в соответствии с теорией чистых ожиданий на рынке устанавливается положение равновесия относительно доходности, которую может получить инвестор, преследую ту или иную стратегию. Чтобы такая ситуация действительно возникла на рынке, форвардная ставка должна быть равна ожидаемой ставке спот.

Проиллюстрируем сказанное на примере. Допустим, инвестиционный горизонт вкладчика составляет 4 года. Доходность четырехлетней облигации равна 10%. Купив данную облигацию, вкладчик обеспечит себе доходность из расчета 10° о годовых. Одновременно он имеет другие варианты:

а) последовательно купить в течение четырех лет четыре годичные облигации;

б) две двухгодичные облигации;

в) одну трехгодичную и одну одногодичную облигации;

г) одну одногодичную и одну трехгодичную облигации.

Все перечисленные стратегии должны принести инвестору одинаковую доходность. В противном случае он предпочтет более доходную менее доходной. Допустим, инвестор решил купить последовательно две двухгодичные облигации. Доходность двухлетней облигации равна 9%. Чтобы он оказался безразличен к выбору отмеченной стратегии или четырехлетней бумаги, должно выполняться равенство

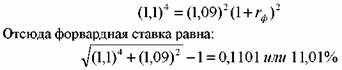
Таким образом данная теория объясняет форму кривой доходности? Если кривая поднимается вверх, это говорит о том, что по мере увеличения времени форвардные ставки возрастают. Это, в свою очередь, означает ожидание роста в будущем процентных ставок по краткосрочным бумагам. Если кривая направлена вниз, то форвардные ставки падают с течением времени. Это говорит о том, что инвесторы ожидают в будущем падения ставок по краткосрочным бумагам. Если кривая доходности параллельна оси абсцисс, то форвардные ставки и текущие ставки спот по краткосрочным бумагам равны, т. е. вкладчики ожидают, что ставки по краткосрочным бумагам в будущем не изменятся.

Теория предпочтения ликвидности

Данная теория полагает: инвесторы не безразличны к срокам до погашения облигаций, а предпочитают краткосрочные бумаги долгосрочным, поскольку они несут меньше риска. Краткосрочные облигации более привлекательны для вкладчиков, поэтому они готовы платить за них дополнительную сумму денег, которая называется премией за ликвидность. В результате доходность краткосрочных бумаг ниже долгосрочных. В свою очередь, долгосрочные облигации должны быть более доходными, чтобы вкладчики согласились их приобретать. Это означает, что инвестор получит более высокую доходность, если приобретет долгосрочную бумагу вместо последовательной покупки краткосрочных бумаг в течение того же периода времени. Такая ситуация будет наблюдаться, когда форвардная ставка больше будущей ожидаемой ставки спот для этого же периода. Разница между ними равна премии за ликвидность.

Таким образом, если полагаться на данную теорию для оценки будущих ставок спот, то следует учитывать, что форвардная ставка будет выше ожидаемой ставки спот по краткосрочным бумагам. Каким образом объясняет форму кривой доходности рассматриваемая теория? Если ставки по краткосрочным бумагам ожидаются неизменными, кривая доходности будет плавно подниматься вверх, поскольку по краткосрочным бумагам инвестор уплачивает премию за ликвидность, и, следовательно, доходность долгосрочных бумаг должна быть выше краткосрочных. Некоторый подъем кривой доходности в этом случае связан только с премией за ликвидность. Если кривая круто идет вверх, это происходит вследствие, во-первых, премии за ликвидность и, во-вторых, ожиданий более высокой ставки процента по краткосрочным бумагам в будущем. Если кривая параллельна оси абсцисс или направлена вниз, то это говорит о том, что ожидается падение будущих ставок.

Теория сегментации рынка

Основным положением теории является тезис: рынок облигаций поделен на сегменты, в которых действуют определенные участники. Каждый сегмент представляет собой нишу для каждого участника в силу объективных экономических или законодательных ограничений. На рынке облигаций преобладают крупные институциональные инвесторы, имеющие свои предпочтения. Так, коммерческие банки инвестируют средства большей частью в краткосрочные бумаги, чтобы иметь наиболее ликвидные активы для обслуживания требований по вкладам; страховые организации, страхующие от несчастных случаев, сосредотачивают свое внимание на среднесрочных бумагах; организации, страхующие жизнь, предпочитают долгосрочные инвестиции и т. д. В связи с этим на ставку процента воздействует спрос и предложение финансовых ресурсов в рамках каждого сегмента, а не рынка в целом, т. е. нет прямой взаимосвязи между уровнем кратко-, средне- и долгосрочных ставок. Это, естественно, не означает, что тот или иной инвестор не выходит за рамки своей ниши. В случае более выгодной ситуации в соседнем сегменте вкладчик скорее всего расширит границы своей ниши, но не намного.

Теория сегментации объясняет форму кривой доходности преимущественно как результат взаимодействия спроса и предложения облигаций в каждом сегменте, поскольку участники рынка имеют свои временные предпочтения и подвержены определенным законодательным ограничениям. Ожидания будущего развития конъюнктуры также принимаются во внимание, но в меньшей степени.

Краткие выводы

Кривая доходности представляет собой зависимость доходности облигаций от срока их погашения.

Спотовая процентная ставка для периода в п лет — это ставка для облигации с нулевым купоном, до погашения которой осталось п лет. Зная ставку спот для п лет, цену купонной облигации со временем погашения n + 1 год, можно рассчитать теоретическую ставку спот для п + 1 года.

Форвардная ставка — это ставка для некоторого периода в будущем. Она определяется ставкой спот. Если на рынке наблюдается восходящая форма кривой доходности, форвардная ставка будет превышать ставку спот и доходность купонной облигации. Если кривая доходности направлена вниз, то форвардная ставка ниже спотовой и доходности купонной облигации.

Теория чистых ожиданий полагает: инвесторы не имеют предпочтений относительно облигаций с каким-либо определенным сроком погашения в рамках своего инвестиционного горизонта. Согласно этой теории текущая форвардная ставка для некоторого периода времени равна ожидаемой будущей ставке спот для этого же периода. Теория предпочтения ликвидности говорит: инвесторы предпочитают краткосрочные бумаги долгосрочным, поскольку они несут меньше риска, и поэтому готовы платить за них более высокую цену. В соответствии с теорией форвардная ставка будет больше будущей ожидаемой ставки спот для этого же периода при восходящей форме кривой доходности.

Теория сегментации рынка полагает: рынок поделен на сегменты, в которых действуют определенные участники, и они в основном не выходят за пределы своей ниши. Поэтому ставка процента определяется спросом и предложением в рамках каждого сегмента, а не рынка в целом, и нет прямой взаимосвязи между уровнем кратко-, средне- и долгосрочных ставок.