Это уравнение представляет собой уравнение прямой координатах

ln(c(x)) – (x₁-x). Найдя из графика тангенс угла наклона прямой линии a, можно рассчитать критерий Пекле по формуле tg(a)=Pe, зная критерий Пекле, можно рассчитать коэффициент обратной диффузии по формуле:

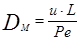(3.4.30)

Таким образом, для определения критерия Ре необходимо определить ряд концентраций трассера по лине аппарата и отложить их в координатах ln(c(x)) – (x₁-x) и из полученной прямой определить критерий Пекле из тангенса угла наклона полученной прямой. Одновременно определяется адекватность применения диффузионной модели для описания движения потока в данном аппарате.

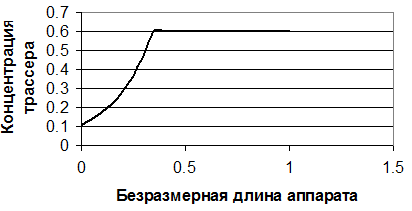
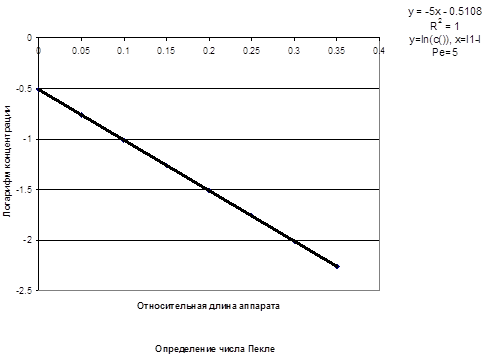
Рис.3.11. Определение числа Пекле методом стационарного ввода трассера.

3.5.Комбинированные модели

Не все реальные процессы могут быть описаны с помощью рассмотренных моделей. К таким процессам относятся процессы, включающим байпасные и циркуляционные потоки, а также застойные зоны. При построении комбинированных моделей принимают, что аппарат состоит из отдельных зон, соединенных между собой последовательно или параллельно, причем каждая из зон может быть описана одной из рассмотренных выше идеальных моделей. Следует отметить, что увеличением количества зон можно описать процесс любой сложности, однако полученное при этом математическое описание получается достаточно сложным для анализа. Рассмотрим несколько типов комбинированных моделей.

Модель с застойной зоной

Застойная зона – это участок в объеме аппарата, в котором происходит слабое перемешивание и обмен этого участка с остальным объемом аппарат затруднен. В соответствии с этим допущением весь объем аппарата может быть разделен на две части – хорошо перемешиваемый объем V_o и объем застойной зоны V_зз.

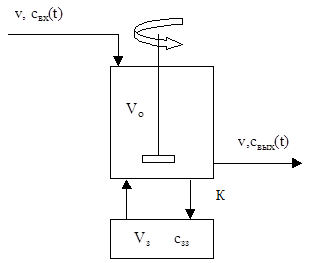
Рис.3.5.1 Схема аппарата с застойной зоной.

V_o – объем части аппарата идеального смешения,

V_зз – объем застойной зоны, с_зз – концентрация в застойной зоне

v- объемный расход смеси через аппарат, К – коэффициент обмена между застойной и перемешиваемой частями аппарата, с_вх(t), с_вых(t), - концентрация на входе и выходе из аппарата

Для получения математической модели составим обобщенное уравнение материального баланса для каждой зоны.

· Для хорошо перемешиваемой зоны:

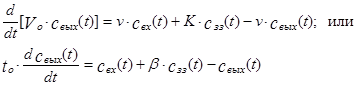(3.5.1)

где t_o – время пребывания в хорошо перемешиваемой зоне, b = K/v- коэффициент, учитывающий интенсивность обмена проточной части с застойной зоной.

· Для застойной зоны

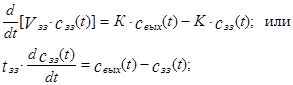(3.5.2)

Где t_зз=V_зз/K – среднее время пребывания вещества в объеме застойной зоны..

Преобразуем уравнения (3.68) и (3.69) по Лапласу:

t_o×p×c_вых(р)=с_вх(р)+b×с_зз(р)-с_вых(р);

(3.5.3)

t_зз×p×c_зз(р)=с_вых(р)-×с_зз(р);

Из второго уравнения системы (3.70) найдем с_зз(р)

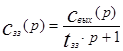
и подставим его в первое уравнение системы:

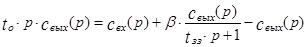(3.5.4)

Из уравнения (3.5.4) найдем передаточную функцию модели с застойной зоной в следующем виде

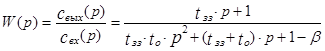(3.5.5)

Полученная передаточная функция соответствует модели идеального смешения с застойной зоной . На рис.3.5.2 показаны кривые разгона модели идеального перемешивания и модели с застойной зоной при равных общих объемах аппаратов. Для аппарата с с застойной зоной характерно более быстрое изменение в начальные моменты времени и более медленное изменение в конце процесса. Появляется затянутый «хвост» кривой, соответствующий медленному вымыванию трассера из застойной зоны.

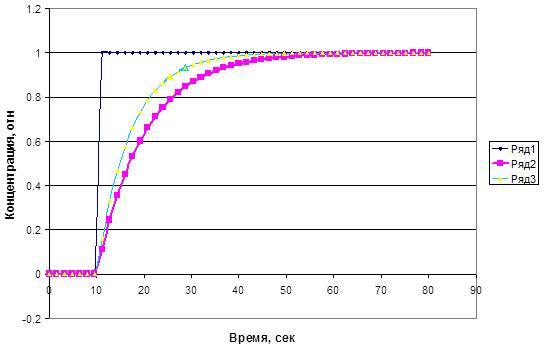
Рис.3.5.2. Кривые разгона аппарата идеального вытеснения (Ряд-2) и аппарата с застойной зоной (Ряд 3) при ступенчатом возмущении на входе (Ряд 1)