Стационарный метод определения критерия Пекле.

Суть этого метода заключается в следующем. На некотором расстоянии от начала аппарата x=x₁ вводится трассер с постоянной скоростью.

Когда процесс станет установившимся, т.е. ¶c(x,t)/¶t=0, будет наблюдаться некоторое стационарное распределение концентрации трассера, Это распределение будет описываться стационарным уравнением диффузионной модели, которое получается из уравнения (3.49):

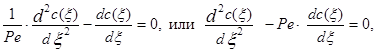(3.4.25

Решением уравнения (3.62) будет уравнение вида:

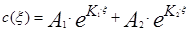(3.4.26)

где А₁ и А₂ постоянные интегрирования, которые находятся из граничных условий, соответствующих условиям проведения эксперимента, а К₁ и К₂ корни характеристического уравнения соответствующего исходному дифференциальному уравнению (3.4.25) характеристическое уравнение будет иметь вид: К²-РеК=0. Корни могут быть определены следующим образом:

К(К-Ре)=0. Тогда К₁=0, К₂=Ре. С учетом этого уравнение (3.4.26) примет вид:

с(x)=А₁+А₂×е^Ре×x (3.4.27)

Для нахождения А₁ воспользуемся первым граничным условием:

,

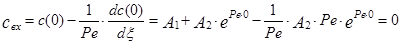Откуда следует, что А₁=0, так как концентрация трассера на входе в аппарат равна нулю. Для нахождения А₂ воспользуемся вторым граничным условием, а именно: при x=x₁ с(x)=с(x₁), следовательно, с(x₁)=А₂×e^Pe×x1, или

А₂=с(x₁)×е^-Реx1. Подставляя найденные значения постоянных интегрирования в (3.4.27), получим уравнение для описания стационарного профиля концентрации трассера:

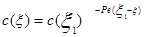(3.4.28)

Логарифмируя выражение (3.4.28), получим следующее уравнение:

ln(c(x))=ln(c(x₁)) – Ре(x₁-x) (3.4.29)