Внутренние силовые факторы в балках при изгибе

Рассмотрим балку, лежащую на двух опорах, к которой приложена сила Р (рис. 8.8). Балка испытывает плоский поперечный изгиб. Для определения внутренних усилий воспользуемся методом сечений. Проведем мысленно сечение mnна расстоянии z от левой опоры и рассмотрим в равновесии левую часть. Реакция А уравновешивается потоком касательных напряжений, направленных вниз.

Равнодействующую потока внутренних касательных напряжений принято называть поперечной силой.

ΣF_y = 0, 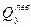= A

Для того чтобы полностью уравновесить левую часть балки в поперечном сечении возникают нормальные усилия.

При изгибе верхние волокна рассматриваемой балки укорачиваются, нижние удлиняются. Следовательно, направление этих усилий – противоположное. В противном случае не выполняется условие:

ΣF_z = 0

Нормальные усилия образуют момент противоположно направленный моменту, образованному силами A и Q_y.

Момент внутренних нормальных усилий в сечении балки называется изгибающим моментом.

M_x^лев = A·z

Рассматривая равновесие правой части балки, видим, что поток касательных усилий в сечении направлен вверх. Равнодействующая этих напряжений

Q_y^прав = P - B

Учитывая, что Р – В = А, видим что поперечная сила в левой и правой части сечения mn одинакова, но направлена в противоположные стороны.

Сложив две части балки, получим равновесную систему.

Аналогично можно показать, что изгибающий момент в правой отсечения части равен изгибающему моменту в левой части.

M_x^прав = B·(a + b – z) - P·(a – z) = Az

Поперечная сила в сечении балки равна сумме проекций всех сил, взятых по одну сторону от сечения, на направление перпендикулярное продольной оси стержня, и взятых с определенным знаком.

Для поперечной силы принято следующее правило знаков (рис. 8.9а).

Изгибающий момент равен сумме моментов всех сил и пар сил, расположенных по одну сторону от сечения и взятых с определенным знаком. Изгибающий момент считается положительным, если он вызывает растяжение нижних волокон балки (рис. 8.9в).