Данные и их структуры.
ИНФОРМАТИКА И СОВРЕМЕННЫЕ
ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ
Общие сведения.
Информатикой называется прикладная инженерная дисциплина, изучающая основные формы представления и способы обработки информации в современных компьютерных системах, аппаратное и программное обеспечение этих систем, а также основные принципы их функционирования.
Исходя из этого определения, предметом исследования дисциплины информатики являются следующие разделы:
- основные формы представления информации;
- основные способы обработки информации;
- современные компьютерные системы;
- основные принципы их функционирования.
Основные формы представления информации. Понятие информации является основным в дисциплине «Информатика» и вытекает из самого ее названия. Однако здесь необходимо отметить, что, несмотря на то, что с этим понятием мы сталкиваемся ежедневно, строго научного, общепринятого определения понятия информации не существует. Это объясняется тем, что понятие информации наряду с понятиями материи и энергии является первичными и неопределяемым в рамках современной науки понятием.
С практической точки зрения информация всегда выступает в виде информационных сообщений (сигналов), которые являются ее материальными носителями. Это, в свою очередь, предполагает наличие:
- источника информации;
- приемника информации;
- канала передачи информации.
Без этих основных элементов информация не существует.
Информационные сообщения от источника информации к приемнику всегда выступают в материально-энергетической форме: электромагнитной, световой, звуковой и т.д. И могут передаваться в двух формах: непрерывный (аналоговый), дискретный (цифровой).
Зарегистрированные дискретные (цифровые) информационные сообщения образуют данные. Таким образом, в «Информатике» информация представляется в виде набора данных, которые и обрабатываются современными компьютерными системами.
Основные способы обработки информации (данных) имеет очень широкий диапазон, который включает в себя следующие основные операции:
сбор, накопление, сортировка, преобразование, хранение и т.д.
Современные компьютерные системы – это совокупность различных технических устройств для обработки информации (данных). Они включают в себя:
- современные персональные компьютеры;
- современные компьютерные сети.
Современные персональные компьютеры представляют собой технические устройства индивидуального пользования для обработки информации (английское слово COMPUTER обозначает устройство для обработки информации).
Современные компьютерные сети представляют собой распределенные технические устройства для обработки информации.
Современные компьютерные системы представляют собой совокупность двух равноправных составляющих: аппаратного (HARDWARE) и программного (SOFTWARE) обеспечения, которые взаимодействуют в процессе обработки информации.
Аппаратное обеспечение (HARDWARE) – это набор технических средств (аппаратуры), обеспечивающих обработку информации в современных компьютерных системах.
Программное обеспечение (SOFTWARE) – это набор программ, обеспечивающих функционирование аппаратного обеспечения современных компьютерных систем по обработке информации. Без программного обеспечения современные компьютерные системы не могут функционировать (превратятся в «мертвое железо»).
Основные принципы функционирования современных персональных компьютеров были разработаны американским математиком фон-Нейманом в 1945 г. и включает в себя:
- принцип программного управления
- принцип разделения вычислительная система на устройства управления (УУ), арифметико-логическое устройство (АЛУ), устройств памяти (УП), устройство ввода (Увв), устройства вывода (Увыв).
- принцип двоичного кодирования
Данные и их структуры.
Как было показано, данные представляют собой зарегистрированные дискретные информационные сообщения и являются составной частью информации. При этом физический метод регистрации может быть любым: механическим, электромагнитным, оптическим и т.д.
В соответствии с методом регистрации данные могут фиксироваться и храниться на носителях различных типов: бумаге, бумажной ленте, магнитной ленте, магнитном диске, оптическом диске и др.
При работе с большим количеством данных возникает проблема их упорядочивания, т.е. образования из них определенных структур. При этом приходится решать проблемы разделения данных между собой и их адресации. Исходя из этого, существует три основных типа структур данных:
- линейные;
- табличные;
- иерархические.
Линейные структуры – это хорошо знакомые списки данных, например, список фамилий работников какого-то учреждения:
1. Иванов А.В.
2. Сидоров В.П.
3. Петров А.П.
Каждая фамилия - это элемент списка, и ее можно разыскать по номеру строки. Этот список можно также представить в виде непрерывной строки:
Иванов А.В., Сидоров В.П., Петров А.П.
Здесь каждый элемент отделен друг от друга разделителем (запятой) и он может быть разыскан по своему порядковому номеру. Еще проще искать отдельные элементы списка, если каждый из них будет иметь одинаковую длину. В этом случае разделители между отдельными элементами списка вообще не нужны. Такой упорядоченный список данных, состоящий из элементов одинаковой длины, называется вектором данных.
Табличные структуры отличаются от линейных тем, что элементы данных определяются в них адресом ячейки, где они расположены. Например, в таблице умножения адрес ячейки, в которой располагается искомое число, определяется номером строки и номером столбца.
При хранении табличных данных количество разделителей может быть больше, чем данных (таблица 1.2.1).
Таблица 1.2.1
| № п/п | Ф.и.о. | Должность | Табельный номер | Оклад (руб.) |
| Иванов А.В. | Ст. инженер | |||
| Сидоров В.П. | Инженер | |||
| Петров А.П. | Техник |
Здесь разделителями являются линии горизонтальной и вертикальной разметки.
Если нужно сохранить таблицу в виде одной длинной символьной строки, используются два символа-разделителя: один – для разделения элементов одной строки, а другой – для разделения строк между собой. Например, таблицу 1.2.1 можно представить следующим образом:
№ п/п * Ф.и.о. * Должность * * Табельный номер * Оклад ** 1* Иванов А.В. * Ст. инженер * 0001 * 5500 ** и т.д.
Еще проще выглядит табличная структура, если все элементы будут иметь равную длину. Такие табличные структуры называются матрицами. В матрицах разделители не нужны.
Линейные и табличные структуры данных являются простыми, и ими легко пользоваться, поскольку адрес каждого элемента задается одним числом (для списка) или двумя числами (для двухмерной таблицы). Они также легко упорядочиваются. Основным методом упорядочивания в них является сортировка, причем данные можно сортировать по любому избранному признаку: по алфавиту, по возрастанию порядкового номера или по возрастанию табельного номера и т.д. Однако у простых структур есть один очень серьезный недостаток – их трудно обновлять. Если, например, в списке сотрудников предприятия необходимо исключить одного сотрудника, то это будет связано с изменением порядковых номеров других сотрудников и т.д. Таким образом, при исключении или добавлении произвольного элемента в упорядоченную линейную или табличную структуру, может происходить изменение адресных данных у других элементов.
Иерархические структуры данных – это структуры, которые трудно представить в виде списка или таблицы. Классическим примером иерархической структуры является система почтовых адресов: код города, город, почтовое отделение, улица, дом, квартира (рис. 1.2.2).
 |
Рис. 1.2.2. Иерархическая структура почтовых адресов
В иерархической структуре адрес каждого элемента определяется путем доступа (маршрутом), ведущим от вершины структуры к данному элементу.
Иерархические структуры данных по своей форме сложнее, чем линейные и табличные структуры, но они не создают проблем с обновлением данных. Недостатком иерархических структур является относительная трудоемкость записи адреса элемента данных и сложность их упорядочивания. Часто методы упорядочивания в таких структурах основываются на предварительной индексации, которая заключается в том, что каждому элементу данных присваивается свой уникальный индекс, который можно использовать при поиске, сортировке и т.д.
Системы счисления.
В современных компьютерных системах исходные данные обычно представляются в десятичной системе счисления. Однако десятичная система не может непосредственно использоваться, так как не существует надежных и быстродействующих технических устройств, которые могли бы фиксировать десять устойчивых состояний. Исходя из этого, в современных компьютерных системах применяются элементы, которые имеют два устойчивых состояния: включен – выключен, есть напряжение – нет напряжения, есть заряд – нет заряда и т.д. Очевидно, что эти два устойчивых состояния удобно описывать двоичной системой счисления, которая имеет всего две цифры (0 и 1) и которая является основной. В качестве вспомогательной системы счисления используется шестнадцатеричная система счисления.
Системой счисления называется совокупность символов (цифр) и правил для изображения чисел.
Используемые в современных компьютерных системах десятичная, двоичная и шестнадцатеричная системы счисления являются позиционными системами, в которых значения отдельных цифр в числе (их вес) определяется их положением (разрядом).
Любая позиционная система счисления характеризуется своим основным параметром – основанием (базисом) – Р.
Основанием (Р) любой позиционной системы счисления называется количество цифр, используемых для изображения чисел.
Так, в десятичной системе счисления основание (Р) равно десяти (Р=10), и, следовательно, в ней используется десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8. 9.
В двоичной системе счисления основание равно двум (Р=2), и, следовательно, в ней используется всего две цифры: 0,1.
В шестнадцатеричной системе счисления основание равно шестнадцати (Р=16), и, следовательно, в ней используется шестнадцать цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15. Для удобства цифры 10, 11, 12, 13, 14, 15 заменены латинскими буквами А, В, С, D, Е, F (А=10, В=11, С=12, D=13, Е=14, F=15).
Исходя из того, что количество используемых цифр в любой позиционной системе счисления определяется ее основанием (Р), соседние разряды в числе отличаются в Р раз. При этом применяется следующая нумерация разрядов дя целой и дробной частей любого числа:
- в целой части числа нумерация начинается с нулевого разряда и идет справа налево, т.е. 0, 1, 2, 3, 4 и т.д.;
- в дробной части числа нумерация начинается с -1 разряда и идет слева направо, т.е. –1, -2, -3, -4, и т.д. (см таблицу 1.3.1.).
Таблица 1.3.1.
| Р а з р я д ы | |||||||
| -1 | -2 | -3 | -4 | ||||
| Р3 | Р2 | Р1 | Р0 | Р-1 | Р-2 | Р-3 | Р-4 |
Пример 1. Десятичная система счисления (Р=10).
А(10) = 275,578(10) = 2*102 + 7*101 + 5*100 + 5*10-1 +3*10-2 +8*10-3
Пример 2. Двоичная система счисления (Р=2).
А(2) = 111,111(2) = 1*22 + 1*21 + 1*20 + 1*2-1 + 1*2-2 + 1*2-3
Пример 3. Шестнадцатеричная система счисления (Р=16).
А(16) = 28С,35Е(16) = 2*162 + 8*161 + 12*160 + 3*16-1 + 5*16-2 + 14*16-3
Если произвести указанные математические операции, то можно получить десятичное представление взятых чисел.
Рассмотренные простые примеры показывают не только формы записи любого числа в произвольно выбранной системе счисления, но и дают простой способ для перевода чисел, выраженных в двоичной и шестнадцатеричной системах счисления, в десятичную систему счисления.
Для перевода десятичных чисел в двоичную систему счисления удобно использовать таблицу соотношение степеней основания 2 (см. таблицу 1.3.2.):
Таблица 1.3.2.
| Степени двойки | |||||||||
| Десятичные числа |
Пример 4. Перевести десятичное число 640 в двоичную систему счисления
640(10)=29+24+23+22=512+16+8+4
Следовательно: 640(10)=1000011100(2)
Рассмотрим теперь обратную задачу: перевод чисел, выраженных в десятичной системе счисления, в двоичную и шестнадцатеричную системы счисления. Для этого удобно использовать следующую таблицу соответствия.
Таблица 1.31
| Системы счисления | Системы счисления | ||||
| Десятичная | Двоичная | Шестнадцатеричная | Десятичная | Двоичная | Шестнадцатеричная |
| А | |||||
| В | |||||
| С | |||||
| D | |||||
| Е | |||||
| F |
Используя таблицу 1.3.1 можно легко переводить числа из двоичной системы счисления в шестнадцатеричную систему и обратно.
Пример 5. Перевести двоичное число 101.11(2) в шестнадцатеричную
систему счисления.
Запишем данное двоичное число следующим образом:
0101.1100
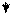 | 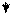 |
5 С
Следовательно 101.11(2) = 5.С(16)
Дата добавления: 2015-12-10; просмотров: 1569;
