Асимптота графика функции, вертикальная, горизонтальная и наклонная асимптоты

Определение 3. Асимптотой графика функции 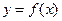называется прямая, график которой неограниченно приближается к графику функции .

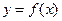Асимптоты делятся на вертикальные, горизонтальные и наклонные.

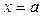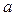Вертикальные асимптоты можно записать в виде , где - точка разрыва функции 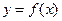, при подходе к которой справа или слева функция стремится к бесконечности.

Горизонтальные и наклонные асимптоты можно записать в виде 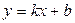. Если угловой коэффициент 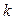равен 0, то это горизонтальная асимптота, если угловой коэффициент 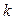не равен 0, то это наклонная асимптота.

Теорема 6. (Критерий существования горизонтальных и наклонных асимптот) Асимптота вида 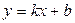существует тогда и только тогда, когда эти числа 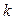и 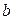можно последовательно найти по формулам: , .

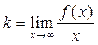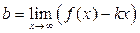Доказательство. Достаточно заметить, что величина 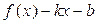является б. м. на бесконечности….. Теорема доказана.

Возможный план исследования функции и построения ее графика

График функции 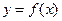будет построен верно, если он отражает характер поведения функции и на нем отмечены все характерные точки графика функции.

Можно предложить такую последовательность действий при построении графика функции.

1) Найти область определения 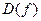функции 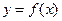, множество ее значений 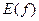, точки пересечения с осями графика функции 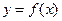, асимптоты графика функции и построить предварительный график функции.

2) Исследовать с помощью первой производной промежутки возрастания, убывания функции, точки экстремума.

3) Исследовать с помощью второй производной промежутки выпуклости, вогнутости графика функции, точки перегиба.