Сущность сложных процентов.
Сложные проценты возрастают с каждым периодом т.к. начисляются на первоначальную сумму долга вместе с процентами, накопленными за все предыдущие периоды:
……………
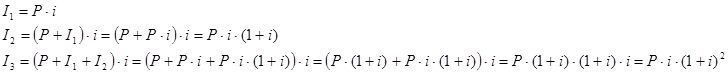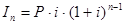
Получили геометрическую прогрессию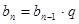 
, сумма членов которой определяется по формуле: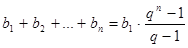 
Общая сумма процентов за весь срок долга находится путем суммирования процентов за периоды:
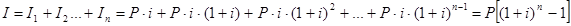
(в данном случае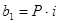 
, 
)
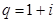Формула сложных процентов:I= P [ (1+i) n - 1]
2.2 Наращение и дисконтирование по сложной ставке.
При начислении сложных процентов с помощью наращения находят наращенную сумму, а с помощью дисконтирования первоначальную сумму долга:
S = P +I = P + P [(1+i) n -1] =P (1+(1+i) n -1) = P (1+i) n
Формула наращения по сложной ставке:S= P (1+i) n ,
где (1+i) n - множитель наращения по сложной ставке, показывает во сколько раз
наращенная сумма S больше первоначальная сумма долга P.
Формула дисконтирования по сложной ставке:P =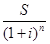 
,
где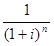 
- дисконтный множитель по сложной ставке, показывает во сколько раз
первоначальная сумма долга P меньше наращенной суммы S.
Если срок долга дробное число, множитель наращения рассчитывают по смешанной схеме, когда за целую часть срока начисляют сложные проценты, а за дробную – простые:
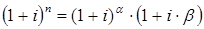, где 
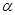- целая часть числа n,
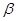- дробная часть
Из формулы наращения выводят формулы для ставки и срока:
S= P (1+i) n
(1+i) n = S/ P
1) размер сложной ставки: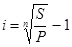 
2) срок долга: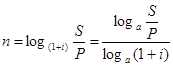 
, где а - любое число.
2.3 Начисление сложных процентов несколько раз в году.
Если сложные проценты начисляются несколько раз в году, то вводится понятие номинальная ставка- это суммарная годовая ставка.
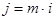, где j - номинальная ставка (годовая),
i - сложная ставка за период начисления,
m - количество начислений за год.
Формула наращения по сложной ставке: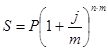 
,
где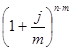 
- множитель наращения по номинальной ставке, показывает во сколько раз
наращенная сумма S больше первоначальная сумма долга P.
Дата добавления: 2015-11-26; просмотров: 1832;