КОНТУРОВ ПРИ ГАРМОНИЧЕСКОМ ВОЗДЕЙСТВИИ
В радиотехнике наряду с одиночными контурами очень часто, особенно в качестве полосовых фильтров, используется система связанных друг с другом контуров. Контуры называются связанными, если электрические процессы, происходящие в них, влияют друг на друга. Связь между контурами может быть емкостная, индуктивная или гальваническая. Наиболее широко используется индуктивная связь, когда переменное магнитное поле катушки первичного контура наводит ЭДС взаимоиндукции в катушку вторичного контура, ток же вторичного контура создает магнитное поле, которое наводит противоЭДС в первичном контуре, что эквивалентно внесению в первичный контур дополнительного сопротивления.
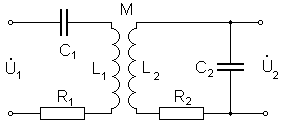
Рис. 1. Индуктивно связанные контуры
Степень взаимного влияния контуров принято оценивать величиной коэффициента связи. В рассматриваемой схеме (рис. 1) коэффициент связи представляет собой отношение части магнитного потока, охватывающего обе катушки, к полному магнитному потоку:
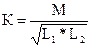 , (1)
, (1)
где 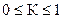 . Величина, равная 1-К, выражает относительную величину потока рассеяния.
. Величина, равная 1-К, выражает относительную величину потока рассеяния.
В некоторых применениях связанных контуров (например, в передатчиках) требуется получить во втором контуре наибольшую мощность электромагнитных колебаний, выделяющуюся на активном сопротивлении. Выясним, при какой величине коэффициента связи поставленное условие будет выполнено, т. е. будет максимум тока во вторичном контуре ( такая связь называется оптимальной).
Запишем уравнения для напряжений каждого контура системы:
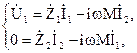 (2)
(2)
где 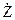 — полное сопротивление контура,
— полное сопротивление контура, 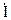 — ток в контуре. Точка сверху показывает комплексный тип переменной величины. Отсюда подстановкой можно получить:
— ток в контуре. Точка сверху показывает комплексный тип переменной величины. Отсюда подстановкой можно получить:
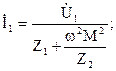
 . (3)
. (3)
Как видно из выражений (3), влияние вторичного контура на первичный можно оценить так называемым «вносимым сопротивлением»:
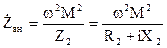 , (4)
, (4)
где 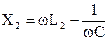 — реактивное, R — активное сопротивление контура.
— реактивное, R — активное сопротивление контура.
График зависимостей мощностей на активных сопротивлениях обоих контуров P=I2R от коэффициента связи K представлен на рис. 2.
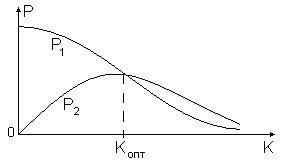
Рис. 2. Зависимость мощности Р в обоих контурах системы от коэффициента связи К
При малых значениях коэффициента связи с его ростом растет и выделяемая во вторичном контуре мощность. При этом вторичный контур незначительно влияет на ток в первичном контуре. С дальнейшим увеличением коэффициента связи увеличивается влияние вторичного контура на первичный, в результате чего мощность и ток в первичном контуре уменьшаются, а вследствие этого начинает уменьшаться и мощность, передаваемая во вторичный контур. Максимальная мощность во вторичном контуре будет при некотором среднем значении коэффициента связи К = Копт.
Для определения Копт и максимального значения тока во вторичном контуре приравняем к нулю производную от его амплитуды по wМ:
 , (5)
, (5)
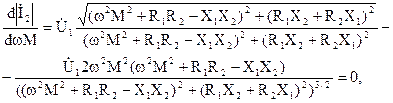 (6)
(6)
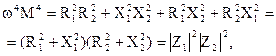 (7)
(7)
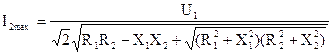 . (8)
. (8)
В общем случае при любых фиксированных значениях параметров контуров изменением коэффициента связи можно добиться выполнения равенств (7) и (8), например, по максимальному показанию вольтметра, подключенного к одному из реактивных элементов второго контура (при постоянной частоте напряжение пропорционально току).
Часто в контурах предусматривается регулировка параметров реактивных элементов с целью увеличения I2max. Например, при регулируемой реактивной составляющей сопротивления только одного контура, приравнивая к нулю производную по Х1 или Х2 из выражения (8), получим дополнительное условие максимума тока I2:
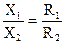 . (9)
. (9)
В этом случае из (7) и (8) будем иметь
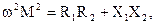
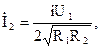
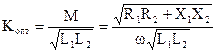 . (10)
. (10)
При этом составляющие вносимого в первичный контур сопротивления Zвн будут равны:
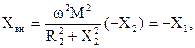
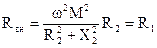 . (11)
. (11)
Ток в первичной цепи будет равен: 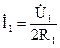 .
.
Таким образом, для источника сигнала система контуров будет представлять чисто активную нагрузку, хотя каждый контур в отдельности в резонанс на частоту сигнала не настроен и имеет реактивные составляющие сопротивления Х1 и Х2. Такой способ настройки контуров называется сложным резонансом. Согласно (9), для получения сложного резонанса контуры должны иметь одинаковые по характеру реактивные сопротивления (оба положительные или оба отрицательные) и относиться друг к другу так же, как и активные сопротивления этих же контуров. Так, для одинаковых контуров эти условия выполняются для любой частоты сигнала. При возможности регулирования реактивных сопротивлений обоих контуров их часто сводят к нулю, т. е. каждый контур в отдельности настраивается в резонанс с частотой сигнала Х1 = Х2 = 0; w01 = w02 = w. При этом
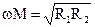 . (12)
. (12)
Такой способ настройки контуров называется полным резонансом. При полном резонансе получаем такое же значение тока во вторичной цепи, как и при сложном резонансе:
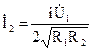 . (13)
. (13)
Однако коэффициент связи, обеспечивающий наибольший ток во вторичном контуре при полном резонансе, будет меньше, т. к. меньшее значение имеет wМ. Согласно (12),
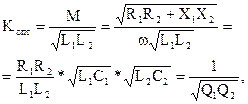 (14)
(14)
где Q1 и Q2 — добротности контуров. Так как обычно добротности контуров Q > 10, то оптимальный коэффициент связи при полном резонансе является величиной малой, Копт. < 0,1.
Рассмотрим частотную характеристику системы связанных контуров, т. е. зависимость отношения U2/U1 от частоты при заданном коэффициенте связи. Для простоты ограничимся случаем идентичных контуров:
L1=L2=L; C1=C2=C; R1=R2=R.
Ток I2 во вторичном контуре согласно (3) равен:
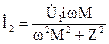 . (15)
. (15)
Тогда напряжение, снимаемое с конденсатора вторичного контура, равно:
 . (16)
. (16)
Отсюда коэффициент передачи системы связанных контуров равен
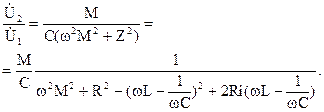 (17)
(17)
Для частоты, близкой к резонансной частоте единичного контура,
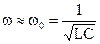 и можно положить
и можно положить
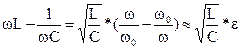 ,
,
где 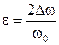 - расстройка контура.
- расстройка контура.
Производя в (17) замену и вводя коэффициент связи, получим
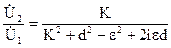 , (18)
, (18)
где 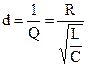 .
.
Для модуля коэффициента передачи (модуль амплитудно-частотной характеристики) имеем:
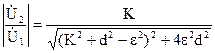 . (19)
. (19)
Найдем частоту (т. е. значении e), при которой модуль коэффициента передачи имеет максимум. Для этого приравняем нулю производную знаменателя по e:

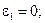
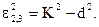 (20)
(20)
При K £ d имеем только одно действительное значение e=0, т. е. w=w0, что соответствует максимуму
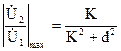 .
.
При d<K и e=0 будет минимум
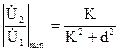 ,
,
а при 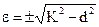 — два боковых максимума (см. рис. 3) и
— два боковых максимума (см. рис. 3) и
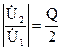 .
.
На частотах, соответствующих боковым максимумам (частоты связи), осуществляется сложный резонанс системы связанных контуров при коэффициенте связи, равном оптимальному. Это же значение коэффициента связи для резонансной частоты будет выше оптимального (как указывалось, оптимальный коэффициент связи при полном резонансе меньше, чем при сложном резонансе). В результате этого при w=w0 и наблюдается минимум амплитудно-частотной характеристики.
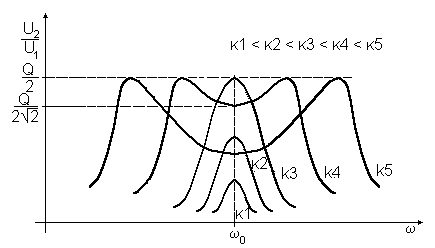
Рис. 3. Амплитудно-частотная характеристика системы связанных контуров
при различных коэффициентах связи
Значение частот связи (при идентичных контурах) можно определить по формуле
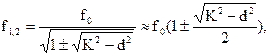
где f0 — резонансная частота, К — коэффициент связи, d=1/Q. При Ккр=d=1/Q связь называется критической, при этом также
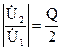 .
.
Как видно, при идентичных контурах критическая связь совпадает с оптимальной связью. При различных контурах
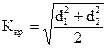 ,
,
в то время как 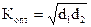 .
.
Отметим, что при критической связи амплитудно-частотная характеристика системы связанных контуров имеет более пологую вершину и более крутые скаты, чем у одиночного контура. Так,
 ,
,
т. е. зависит от 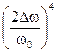 , в то время как у одиночного контура
, в то время как у одиночного контура
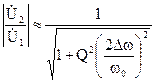 зависит от
зависит от 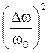 .
.
Для большего уширения вершины контура в центре контура допускают провал, равный (1/2)1/2 максимального значения. При этом
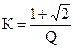 , а
, а 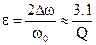 ,
,
т. е. при той же добротности резонансная кривая системы связанных контуров втрое шире, чем при одиночном контуре, но имеет более крутые скаты. При этом скаты резонансной кривой будут гораздо круче, приближаясь к идеальному прямоугольнику.
Такой вид амплитудно-частотной характеристики позволяет без искажений передавать сигнал на частотах в пределах полосы пропускания (например, модулированный сигнал) и практически не пропускать сигнал за пределом полосы пропускания (например, шумы и другие сигналы).
При очень слабой связи (кривая К на рис. 3) полоса пропускания связанных контуров меньше, чем у единичного контура. Это объясняется тем, что при слабой связи обратная реакция второго контура на первый мала, и сигнал как бы последовательно проходит через два независимых контура. При этом колебания, отличающиеся по частоте от резонансной, ослабляются дважды — в первом контуре и во втором. Это позволяет использовать систему связанных контуров для сужения полосы пропускания фильтра.
Дата добавления: 2015-11-06; просмотров: 2578;
