ИССЛЕДОВАНИЕ ПОСЛЕДОВАТЕЛЬНОГО И ПАРАЛЛЕЛЬНОГО КОЛЕБАТЕЛЬНЫХ КОНТУРОВ ПРИ ГАРМОНИЧЕСКОМ ВОЗДЕЙСТВИИ

Последовательный колебательный контур состоит из катушки индуктивности и конденсатора, соединённых последовательно по отношению к источнику переменного напряжения. Эквивалентная схема последовательного контура как двухполюсника, являющегося обычно частью более сложной цепи, приведена на рис. 1, где L — индуктивность, C — конденсатор, R_k — сопротивление потерь в контуре, 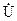— переменное синусоидальное напряжение частотой w в комплексном виде, приложенное к контуру.

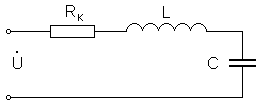
Рис. 1

Используя второй закон Кирхгофа для замкнутой цепи, можно записать

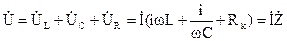, (1)

где 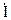— ток в контуре,

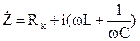(2)

— комплексное сопротивление контура как двухполюсника. Отметим, что комплексная запись синусоидального сигнала U=U_mcos(wt+j_u) есть 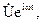где 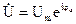. Реальный сигнал есть действительная часть комплексной записи. Комплексное сопротивление двухполюсника есть отношение комплексных амплитуд напряжения и тока:

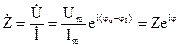, (3)

где 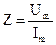, 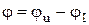. В нашем случае (рис. 2)

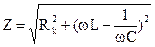, (4)

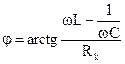. (5)

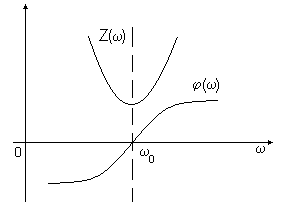
Рис. 2

Часто вместо параметров R_k, C, L вводят следующие характеристики контура:

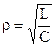— характеристическое сопротивление,

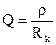— добротность,

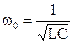— резонансная частота контура.

Записывая комплексное сопротивление контура через характеристики контура, получим:

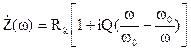. (6)

При частотах, близких к резонансной w ~ w₀,

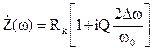, (7)

где Dw=½w-w₀½ — расстройка, сдвиг частоты от резонансной. При w=w₀ и wL=1/wC падение напряжения на емкости и индуктивности полностью нейтрализуют друг друга, и комплексное сопротивление становится минимальным и чисто активным —

,

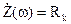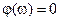
Добротность определяет так называемую полосу пропускания контура 2Dw₀=w₀/Q. При Dw=Dw₀ Z=R_k(2)^1/2, т.е. увеличивается в 1,4 раза.

Рассмотрим использование последовательного колебательного контура как четырёхполюсника — цепи с двумя входами и двумя выходами (рис. 3).

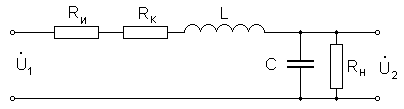
Рис. 3

Для синусоидальных сигналов четырехполюсник характеризуется передаточной функцией (коэффициентом передачи по напряжению), являющейся отношением комплексных амплитуд напряжения на выходе и входе:

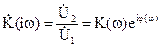, (8)

где .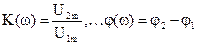

При этом сопротивление нагрузки R_н должно быть много больше выходного сопротивления четырехполюсника. С другой стороны, сопротивление источника сигнала R_и должно быть много меньше входного сопротивления четырехполюсника либо также включатся в схему четырехполюсника. Рассмотрим передаточную функцию такого четырехполюсника с включенным сопротивлением источника нагрузки. Тогда

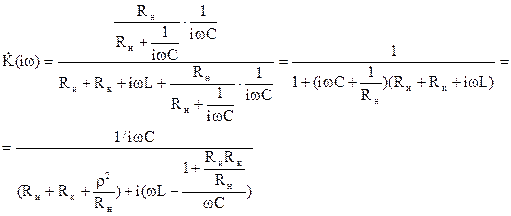(9)

Обычно используют случай r>>R_и+R_к и R_н>r, т. е. 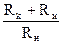<< 1. Тогда

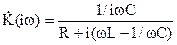, (10)

где R=R_и + R_к + r²/R_н. Таким образом, сопротивление источника суммируется с активным сопротивлением контура, сопротивление нагрузки также вносит дополнительное сопротивление в контур, равное r²/R_н. Эквивалентная схема четырехполюсника представлена на рис. 4.

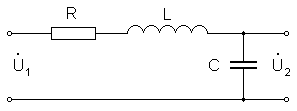
Рис. 4

Используя те же преобразования, будем иметь:

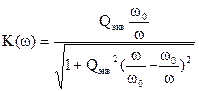. (11)

Для частот близких к резонансной w » w₀

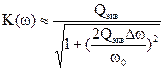, (12)

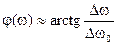, (13)

где 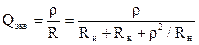— эквивалентная добротность контура, 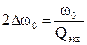— полоса пропускания контура.

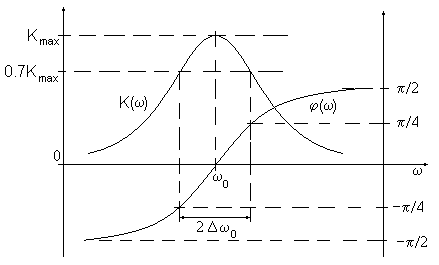
Рис. 5

Зависимость K(w) называется амплитудно-частотной характеристикой четырехполюсника, а j(w) называется фазочастотной характеристикой (рис. 5). Коэффициент передачи на резонансной частоте равен К_max=Q_экв. При Dw » Dw₀ K(w)=Q_экв/(2)^1/2 =0.7Q_экв. На резонансной частоте сдвиг фаз выходного и входного сигнала равен нулю, на границе полосы пропускания ±p/4. Отметим, что ввиду хотя и слабой, но зависимости числителя выражения K(iw) от частоты, за счет множителя w₀/w максимум K(w) несколько смещен относительно резонансной частоты w₀:

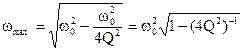. (14)

Это выражение можно получить, дифференцируя выражение (11). Однако это смещение при реальных Q>10 так незначительно, что практически незаметно. На частотах, сильно отличающихся от резонансной частоты, асимметрия K(w) становится заметнее.

2.2. Параллельный колебательный контур.

Цепь, состоящая из индуктивности и емкости, соединенных параллельно друг с другом и источником напряжения, называется параллельным колебательным контуром (рис. 6).

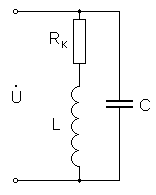
Рис. 6

Найдем комплексное сопротивление контура как двухполюсника:

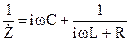или 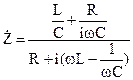. (15)

Вводя здесь также

, ,

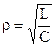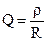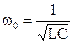
и пренебрегая вторым членом в числителе, т. к. 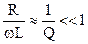при частотах, близких к резонансной, получим

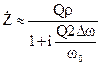. (16)

На резонансной частоте w₀=w комплексное сопротивление максимально и чисто активно. Вспомним, что комплексное сопротивление последовательного колебательного контура на резонансной частоте минимально.

Рассмотрим передаточную функцию параллельного контура как четырехполюсника, вводя в его цепь сопротивление источника сигнала R_и и сопротивление нагрузки R_н (рис. 7).

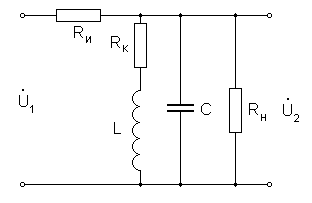
Рис. 7

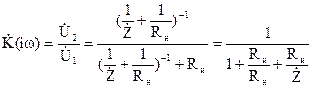. (17)

Подставляя в это выражение сопротивление контура, получим

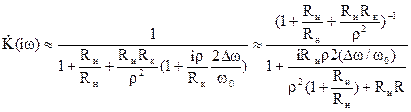. (18)

Или

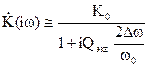, (19)

где 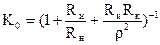. Эквивалентная добротность контура равна

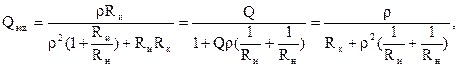(20)

где Q=r/R_к — добротность самого контура. Как видно, все проводимости, подключенные параллельно контуру, в том числе и проводимость источника сигнала, суммируются и уменьшают добротность контура. Частотная зависимость передаточной функции совпадает с передаточной функцией последовательного контура, и обе схемы используются в качестве узкополосного фильтра частот. Отличие заключается в разной зависимости эквивалентной добротности от сопротивления источника сигнала. При R_и<<r необходимо использовать последовательный контур. При R_и>>r — параллельный. При R_и»r используют параллельный контур, но последовательно источнику ставят дополнительное сопротивление. Величина добротности самого контура зависит от его элементов, величины нагрузки и наличия сердечника. Амплитудно-частотная и фазочастотная характеристики параллельного контура получаются преобразованием выражения (19) и равны

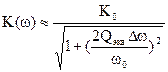, (21)

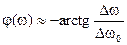. (22)

Коэффициент передачи на резонансной частоте равен K_max=K₀, а на границах полосы пропускания 0.7K₀. Фазочастотная характеристика имеет инверсный вид по сравнению с последовательным контуром. С увеличением частоты от нуля до частот гораздо больших резонансной фаза изменяется от p/2 до -p/2.