Анализ различий
Проверка существенности различий заключается в сопоставлении ответов на один и тот же вопрос, полученных для двух или более независимых групп респондентов. Кроме того, в ряде случаев представляет интерес сравнение ответов на два или более независимых вопросов для одной и той же выборки.
Примером первого случая может служить изучение вопроса: что предпочитают пить по утрам жители определенного региона: кофе или чай. Первоначально было опрошено на основе формирования случайной выборки 100 респондентов, 60% которых отдают предпочтение кофе; через год исследование было повторено, и только 40% из 300 опрошенных человек высказалось за кофе. Как можно сопоставить результаты этих двух исследований? Прямым арифметическим путем сравнивать 40% и 60% нельзя из-за разных ошибок выборок. Хотя в случае больших различий в цифрах, скажем, 20 и 80%, легче сделать вывод об изменении вкусов в пользу кофе. Однако если есть уверенность, что эта большая разница обусловлена прежде всего тем, что в первом случае использовалась очень малая выборка, то такой вывод может оказаться сомнительным. Таким образом, при проведении подобного сравнения в расчет необходимо принять два критических фактора: степень существенности различий между величинами параметра для двух выборок и средние квадратические ошибки двух выборок, определяемые их объемами.
Для проверки, является ли существенной разница измеренных средних, используется нулевая гипотеза. Нулевая гипотеза предполагает, что две совокупности, сравниваемые по одному или нескольким признакам, не отличаются друг от друга. При этом предполагается, что действительное различие сравниваемых величин равно нулю, а выявленное по данным отличие от нуля носит случайный характер [10], [25].
Для проверки существенности разницы между двумя измеренными средними (процентами) вначале проводится их сравнение, а затем полученная разница переводится в значение среднеквадратических ошибок, и определяется, насколько далеко они отклоняются от гипотетического нулевого значения.
Как только определены среднеквадратические ошибки, становится известной площадь под нормальной кривой распределения и появляется возможность сделать заключение о вероятности выполнения нулевой гипотезы.
Рассмотрим следующий пример. Попытаемся ответить на вопрос: «Есть ли разница в потреблении прохладительных напитков между девушками и юношами?». При опросе был задан вопрос относительно числа банок прохладительных напитков, потребляемых в течение недели. Описательная статистика показала, что в среднем юноши потребляют 9, а девушки 7,5 банок прохладительных напитков. Средние квадратические отклонения, соответственно, составили 2 и 1,2. Объем выборок в обоих случаях составлял 100 человек. Проверка статистически значимой разницы в оценках осуществлялась следующим образом:
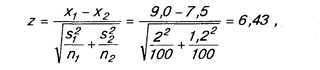
где x1 и x2 — средние для двух выборок;
s1 и s2 — средние квадратические отклонения для двух выборок;
n1 и n2 — объем соответственно первой и второй выборки.
Числитель данной формулы характеризует разницу средних. Кроме того, необходимо учесть различие формы двух кривых распределения. Это осуществляется в знаменателе формулы. Выборочное распределение теперь рассматривается как выборочное распределение разницы между средними (процентными мерами). Если нулевая гипотеза справедлива, то распределение разницы является нормальной кривой со средней, равной нулю, и средней квадратической ошибкой, равной 1.
Видно, что величина 6,43 существенно превышает значение ±1,96 (95%-ный уровень доверительности) и ±2,58 (99%-ный уровень доверительности). Это означает, что нулевая гипотеза не является истинной.
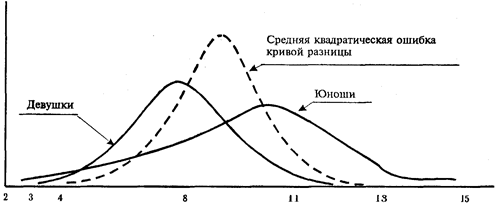
На рис. 4.6 приводятся кривые распределения для этих двух сравниваемых выборок и средняя квадратическая ошибка кривой разницы. Средняя квадратическая ошибка средней кривой разницы равна 0. Вследствие большого значения среднеквадратических ошибок вероятность справедливости нулевой гипотезы об отсутствии разницы между двумя средними меньше 0,001.
Дата добавления: 2015-09-11; просмотров: 1169;
