Статистический вывод
Вывод является видом логического анализа, направленного на получение общих заключений о всей совокупности на основе наблюдений за малой группой единиц данной совокупности.
Выводы делаются на основе анализа малого числа фактов. Например, если два ваших товарища, имеющих одну и ту же марку автомобиля, жалуются на его качество, то вы можете сделать вывод о низком качестве данной марки автомобиля в целом.
Статистический же вывод основан на статистическом анализе результатов выборочных исследований и направлен на оценку параметров совокупности в целом. В данном случае результаты выборочных исследований являются только отправной точкой для получения общих выводов.
Например, автомобилестроительная компания провела два независимых исследования с целью определения степени удовлетворенности потребителей своими автомобилями. Первая выборка включала 100 потребителей, купивших данную модель в течение последних шести месяцев. Вторая выборка включала 1000 потребителей. В ходе телефонного интервьюирования респонденты отвечали на вопрос: «Удовлетворены вы или не удовлетворены купленной вами моделью автомобиля?» Первый опрос выявил 30% неудовлетворенных, второй — 35%.
Поскольку существуют ошибки выборки и в первом и во втором случаях, то можно сделать следующий вывод. Для первого случая: около 30% опрошенных выразили неудовлетворенность купленной моделью автомобиля. Для второго случая около 35% опрошенных выразили неудовлетворенность купленной моделью автомобиля. Какой же общий вывод можно сделать в данном случае? Как избавиться от термина «около»? Для этого введем показатель ошибки: 30% ± х% и 35% ± у% и сравним х и у. Используя логический анализ, можно сделать вывод, что большая выборка содержит меньшую ошибку и что на ее основе можно сделать более правильные выводы о мнении всей совокупности потребителей. Видно, что решающим фактором для получения правильных выводов является размер выборки. Данный показатель присутствует во всех формулах, определяющих содержание различных методов статистического вывода.
При проведении маркетинговых исследований чаще всего используются следующие методы статистического вывода: оценка параметров и проверка гипотез.
Оценка параметров генеральной совокупности представляет из себя процесс определения, исходя из данных о выборке, интервала, в котором находится один из параметров генеральной совокупности, например среднее значение. Для этого используют следующие статистические показатели: средние величины, среднюю квадратическую ошибку и желаемый уровень доверительности (обычно 95% или 99%).
Ниже пойдет разговор об их роли при проведении оценки параметров.
Средняя квадратическая ошибка является, как отмечалось выше, мерой вариации выборочного распределения при теоретическом предположении, что исследовалось множество независимых выборок одной и той же генеральной совокупности.
Она определяется по следующей формуле:
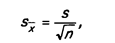
 где sx — средняя квадратическая ошибка выборочной средней;
где sx — средняя квадратическая ошибка выборочной средней;
s — среднее квадратическое отклонение от средней величины в выборке;
n — объем выборки.
Если используются процентные меры, выражающие альтернативную изменчивость качественных признаков, то

где s — средняя квадратическая ошибка выборочной средней при использовании процентных мер;
р — процент респондентов в выборке, поддержавших первую альтернативу;
q = (100 — q) — процент респондентов в выборке, поддержавших
вторую альтернативу;
n — объем выборки.
Видно, что средняя ошибка выборки тем больше, чем больше вариация, и тем меньше, чем больше объем выборки.
Поскольку всегда существует выборочная ошибка, то необходимо оценить разброс значений изучаемого параметра генеральной совокупности. Предположим, исследователь выбрал уровень доверительности, равный 99%. Из свойств нормальной кривой распределения вытекает, что ему соответствует параметр Z = ± 2,58. Средняя для генеральной совокупности в целом вычисляется по формуле
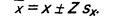
Если используются процентные меры, то
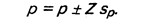
Это означает, что если вы хотите, чтобы при 99%-ном уровне доверительности диапазон оценок включал истинную для генеральной совокупности оценку, то необходимо умножить среднюю квадратическую ошибку на 2,58 и добавить полученный результат к процентному значению р (верхняя предельная оценка). Если же произвести вычитание данного произведения, то найдем нижнюю предельную оценку.
Как эти формулы связаны со статистическим выводом?
Поскольку производится оценка параметра генеральной совокупности, то здесь указывается диапазон, в который попадает истинное значение параметра генеральной совокупности. С этой целью для выборки берутся статистическая мера центральной тенденции, величина дисперсии и объем выборки. Далее делается предположение об уровне доверительности и рассчитывается диапазон разброса параметра для генеральной совокупности.
Например, для членов выборки (100 читателей какой-то газеты) было установлено, что среднее время чтения газеты составляет 45 минут при средней квадратической ошибке в 20 минут. При уровне доверительности, равном 95%-ном, получим

При 99%-ном уровне доверительности получим
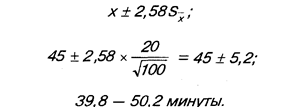
Видно, что доверительный интервал шире для 99% по сравнению с 95%-ным уровнем доверительности.
Если используются проценты и оказалось, что из выборки в 100 человек 50% опрошенных по утрам пьет кофе, то при уровне доверительности в 99% получим следующий диапазон оценок:
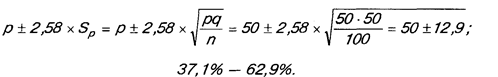
Таким образом, логика статистического вывода направлена на получение конечных заключений об изучаемом параметре генеральной совокупности на основе выборочного исследования, осуществленного по законам математической статистики. Если используется простое заключение, не основанное на статистических измерениях, то конечные выводы носят субъективный характер и на основе одних и тех же фактов разные специалисты могут сделать разные выводы.
При использовании статистического вывода используются формулы, носящие объективный характер, в основе которых лежат общепризнанные статистические концепции. В результате конечные выводы носят намного более объективный характер.
В ряде случаев делаются суждения относительно какого-то параметра генеральной совокупности (величине средней, дисперсии, характере распределения, форме и тесноте связи между переменными) исходя только из некоторых предположений, размышлений, интуиции, неполных знаний. Такие суждения называются гипотезами.
Статистической гипотезой называется предположение о свойстве генеральной совокупности, которое можно проверить, опираясь на данные выборки.
Подпроверкой гипотезы понимается статистическая процедура, применяемая для подтверждения или отклонения гипотезы, основанной на результатах выборочных исследований. Проверка гипотезы осуществляется на основе выявления согласованности эмпирических данных с гипотетическими. Если расхождение между сравниваемыми величинами не выходит за пределы случайных ошибок, гипотезу принимают. При этом не делается никаких заключений о правильности самой гипотезы, речь идет лишь о согласованности сравниваемых данных.
Проверка гипотезы проводится в пять этапов:
1. Делается некоторое предположение относительно какой-то характеристики генеральной совокупности, например о средней величине определенного параметра.
2. Формируется случайная выборка, проводится выборочное исследование и определяются статистические показатели выборки.
3. Сравниваются гипотетическое и статистическое значения исследуемой характеристики.
4. Определяется, соответствуют или нет результаты выборочного исследования принятой гипотезе.
5. Если результаты выборочного исследования не подтверждают гипотезу, последняя пересматривается — она должна соответствовать данным выборочного исследования.
Вследствие вариации результатов выборочных исследований невозможно сделать абсолютно точный вывод о достоверности гипотезы, проводя простое арифметическое сравнение величин характеристик. Поэтому статистическая проверка гипотезы включает использование: выборочного значения характеристики, среднего квадратического отклонения, желательного уровня доверительности и гипотетитеского значения характеристики для генеральной совокупности в целом.
Для проверки гипотез о средних величинах применяется следующая формула:
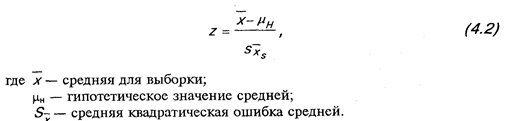
Например, готовя рекламу учебной программы по подготовке торговых агентов в колледже, руководитель программы считал, что выпускники программы получают в среднем 1750 долларов в месяц. Таким образом, гипотетическая средняя для генеральной совокупности равна 1750 долларам. Для проверки данной гипотезы было проведено телефонное обследование торговых агентов разных фирм.
Выборка составила 100 человек, средняя для выборки равнялась 1800 долларам и среднее квадратическое отклонение составляло 350 долларов. Возникает вопрос, является ли большой разница (50 долларов) между гипотетической зарплатой и ее средним значением для выборки. Проводим расчеты по формуле (4.2):
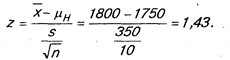
Видно, что средняя квадратическая ошибка средней величины была равна 35 долларам, а частное от деления 50 на 45 составляет 1,43 (нормированное отклонение), что меньше ±1,96 — величины, характеризующей уровень доверительности 95%. В данном случае выдвинутую гипотезу можно признать достоверной.
При использовании процентной меры испытание гипотезы осуществляется следующим образом. Предположим, что, исходя из собственного опыта, один из автолюбителей выдвинул гипотезу, согласно которой только 10% автолюбителей используют ремни безопасности. Однако национальные выборочные исследования 1000 автолюбителей показали, что 80% из них используют ремни безопасности. Расчеты в данном случае проводятся следующим образом:
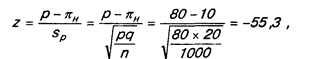
где р — процент из выборочных исследований;
πH — процент из гипотезы;
sp — средняя квадратическая ошибка при расчетах в процентах.
Видно, что первоначальная гипотеза отличалась от найденных 80% на величину 55,3, умноженную на среднеквадратическую ошибку, т.е. не может быть признана достоверной.
В ряде случаев целесообразно использовать направленные гипотезы. Направленные гипотезы определяет направления возможных значений какого-то параметра генеральной совокупности. Например, заработная плата составляет больше 1750 долларов. В данном случае используется только одна сторона кривой распределения, что находит отражение в применении знаков «+» и «-» в расчетных формулах.
Более детальную информацию по данной проблеме можно получить из [25].
Здесь, правда, возникает вопрос. Если можно провести выборочные исследования, то зачем выдвигать гипотезы? Обработка результатов выборочных исследований дает возможность получить средние величины и их статистические характеристики, не выдвигая никаких гипотез. Поэтому проверка гипотез скорее применяется в случаях, когда невозможно или чрезвычайно трудоемко проводить полномасштабные исследования и когда требуется сравнивать результаты нескольких исследований (для разных групп респондентов или проведенных в разное время). Такого рода задачи, как правило, возникают в социальной статистике. Трудоемкость статистико-социологических исследований приводит к тому, что почти все они строятся на несплошном учете. Поэтому проблема доказательности выводов в социальной статистике стоит особенно остро.
Применяя процедуру проверки гипотез, следует помнить, что она может гарантировать результаты с определенной вероятностью лишь по «беспристрастным» выборкам, на основе объективных данных.
Дата добавления: 2015-09-11; просмотров: 934;
