Параметризация уравнения множественной регрессии и его интерпретация

Установив перечень признаков-факторов, и предварительно оценив форму связи, можно записать соответствующее математическое уравнение теоретической линии множественной регрессии. Так, например, в случае двухфакторной линейной регрессии нахождение неизвестных параметров по методу наименьших квадратов предполагает решение системы нормальных уравнений:

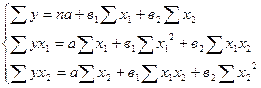
Комментируя решенное уравнение, следует помнить о том, что существует различие в интерпретации коэффициента регрессии в парных и множественных моделях. В уравнениях парной регрессии коэффициент в называют коэффициентом полной регрессии. Он показывает, как в среднем изменится у при изменении х на единицу, при условии, что влияние других факторов не учтено.

В уравнениях множественной регрессии коэффициент в_i называют коэффициентом чистой регрессии. Он измеряет среднее изменение у при изменении фактора х_i на единицу, но при условии, что действие других факторов, включенных в уравнение регрессии, учтено и зафиксировано на среднем уровне.

Коэффициенты регрессии в уравнении связи несопоставимы друг с другом в силу разных единиц измерения. Для целей сравнения и определения приоритетности факторов определяют стандартизованные коэффициенты регрессии: коэффициенты эластичности и бета-коэффициенты.

Коэффициенты эластичности для линейной связи определяются по формулам

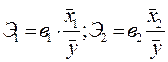и т.д. (5.1.4.)

Они показывают, на сколько процентов изменится признак-результат, если признак-фактор изменится на один процент. Формулы для расчета бета-коэффициентов имеют вид

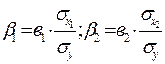(5.1.5)

Величина бета-коэффициента показывает, на сколько средних квадратических отклонений изменится у, если х_i изменится на одно среднее квадратическое отклонение.

Стандартизованные коэффициенты регрессии позволяют выделить приоритетные факторы, в изменении которых заложены наибольшие возможности в управлении изменением результативного признака.

Как и в парной зависимости, возможны разные виды уравнений множественной регрессии: линейные и нелинейные. Ввиду четкой интерпретации параметров уравнения наиболее широко используются линейные и степенные функции. Линейная модель в форме (5.1.1) является аддитивной. Это означает, что в основе модели лежит гипотеза о том, что каждый фактор что-то добавляет или отнимает от значения результативного признака. Например, если у – это урожайность сельскохозяйственной культуры, а х₁, х₂ и х₃ – агротехнические факторы: дозы удобрений, число прополок, поливов и т.п., то каждый из этих факторов либо повышает, либо понижает величину урожайности, причем последняя могла бы существовать и без этих факторов.

Также часто линейная регрессионная модель используется в функциях потребления (спроса), где у – потребление товара или группы товаров, а факторами могут быть доход семьи в текущем и предшествующем периоде, размер семьи, цены, прошлые привычки потребления, то есть потребление товара в предшествующем периоде.

Параметр а в таком уравнении не подлежит экономической интерпретации, а коэффициенты регрессии рассматриваются как характеристики склонности к потреблению. Например, функция потребления имеет вид

П_t = a +b₁D_t + b₂D_t-1 (5.1.6)

где потребление в период времени t зависит от дохода того же периода D_t и от дохода предшествующего периода D_t-1. Коэффициент в₁ называют краткосрочной предельной склонностью к потреблению. Он показывает, на сколько увеличится потребление товара при увеличении доходов текущего периода на единицу. Общим эффектом возрастания как текущего, так и предыдущего дохода будет рост потребления на величину b = b₁ + b₂. Коэффициент в рассматривается здесь как долгосрочная склонность к потреблению.

Пример: П (потребление) = 38 + 0,47Д_т +0,23Д_т-1. Краткосрочная склонность к потреблению составляет здесь 0,47, а долгосрочная склонность 0,47+0,23=0,7.

Однако аддитивная модель пригодна не для любых связей в экономике. Если, например, изучается зависимость объема продукции предприятия от занимаемых площадей, числа работников, стоимости основных фондов (или всего капитала), то каждый из факторов является необходимым для существования результата, а не добавлением к нему. В таких ситуациях нужно исходить из гипотезы о мультипликативной форме модели:

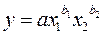(5.1.7)

Такая модель по ее первым создателям получила название модель Кобба-Дугласа. Это степенная функция и, как мы уже знаем, показатели степени при факторах являются коэффициентами эластичности. Они показывают, на сколько процентов изменяется в среднем результат с изменением соответствующего фактора на 1 процент при неизменности других факторов. Решение степенной функции методом наименьших квадратов требует предварительной ее линеаризации. Как было рассмотрено ранее (лекция 4), линеаризация степенных функций проводится с помощью логарифмирования ее переменных.

Степенные множественные функции часто используются как производственные функции, где результатом выступают объемы производства, а факторами – используемые ресурсы (трудовые ресурсы, основные производственные фонды, машины, текущие затраты и т.п.). Экономический смысл здесь имеют не только коэффициенты эластичности по каждому фактору, но и их сумма

B = b₁+b₂ (5.1.8)

Эта величина фиксирует обобщенную характеристику эластичности производства (показывает, на сколько процентов в среднем увеличиваются объемы производства при увеличении всех факторов на 1%).

Возможны и другие линеаризуемые функции для построения уравнения множественной регрессии. Например,

экспонента 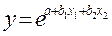(5.1.9)

или гипербола 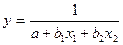(5.1.10)

Стандартные компьютерные программы обработки регрессионного анализа позволяют перебирать различные функции и выбирать ту из них, для которой остаточная дисперсия и ошибка аппроксимации минимальные. Однако следует помнить, что чем сложнее сама функция, тем менее интерпретируемы ее параметры. При сложных полиномиальных функциях необходимо соблюдать соотношение между числом объясняющих переменных и объемом совокупности. Так, полином второй степени с двумя факторами

y = a + b₁x₁ + b₂x₂ +b₁₁x₁²+ b₂₂ x₂ ²+ b₁₂x₁x₂ (5.1.11)

требует не менее 40-50 наблюдений.

Вопросы для повторения по модульной единице 5.1:

1. Назовите условия отбора факторных показателей в уравнение множественной регрессии.

2. Раскройте сущность мультиколлинеарности факторов в модели.

3. Каковы последствия наличия мультиколлинеарных факторов в модели?

4. Назовите методы устранения мультиколлинеарности факторов.

5. Что показывают чистые коэффициенты регрессии?

6. Раскройте назначение стандартизованных коэффициентов регрессии.

7. Как рассчитать средний коэффициент эластичности, и какова его интерпретация?

8. Что показывает бета-коэффициент и как его рассчитать?

9. Как выявить приоритетный фактор(ы) в формировании уровня результативного признака?

10. Функция потребления: сущность, способ решения и интерпретация параметров.

11. Производственная функция: сущность, способ решения и интерпретация параметров.