Метод синфазного и противофазного возбуждения для симметричных восьмиполюсников

Метод синфазного и противофазного возбуждения позволяет свести анализ восьмиполюсников, имеющих плоскость симметрии, к анализу более простых четырехполюсников, представляющих собой «половины» восьмиполюсника. Данное «разделение» представлено на рисунке 3.2,а. В матрице рассеяния восьмиполюсника вследствие симметрии и взаимности независимыми между собой оказываются только шесть элементов:

, , , , , .

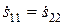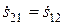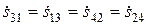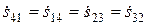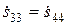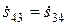Рассмотрим два режима возбуждения восьмиполюсника: синфазный и противофазный.

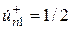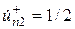1. При синфазном возбуждении со стороны входов 1 и 2 падающими волнами и через плоскость симметрии не происходит передача мощности и в ней устанавливается пучность напряженности касательного электрического поля и нуль распределения напряженного магнитного поля, т.е. создается режим холостого хода. Плоскость как бы расчленяет восьмиполюсник на два не связанных между собой парциальных четырехполюсника синфазного возбуждения, каждый из которых характеризуется матрицей рассеяния 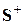, как показано на рисунке 3.2,б.

2. . При противофазном возбуждении со стороны входов 1 и 2 падающими волнам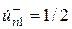и и 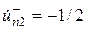через плоскость симметрии нет передачи мощности, в этой плоскости устанавливается нуль распределения напряженности электрического поля и пучность распределения напряженного касательного магнитного поля, т.е. создается режим короткого замыкания. Плоскость симметрии как бы расчленяет восьмиполюсник на два не связанных между собой парциальных четырехполюсника противофазного возбуждения, каждый из которых характеризуется матрицей рассеяния 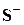, как показано на рисунке 3.2,в.

Матрицы рассеяния парциальных четырехполюсников синфазного и противофазного возбуждения имеют вид:

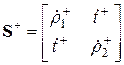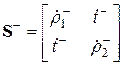, (3.7)

и могут быть определены одна независимо от другой, например, через матрицы передачи, если парциальные четырехполюсники представимы в виде цепочки элементарных каскадов.

Суперпозиция синфазного и противофазного возбуждения входов 1 и 2 восьмиполюсника представляет собой возбуждение одиночного входа 1:

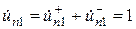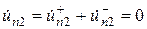, . (3.8)

Учитывая соотношения (3.8), независимые элементы матрицы рассеяния 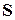восьмиполюсника будут определяться выражениями:

, ,

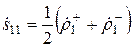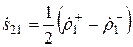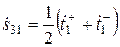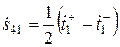, . (3.9а)

Для нахождения элементов 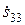и 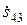матрицы рассеяния 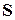повторяются операции синфазного и противофазного возбуждения для входов 3 и 4. В результате имеем:

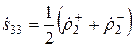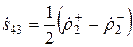, . (3.9б)

При наличии у восьмиполюсника еще одной плоскости симметрии (или же при наличии полной поворотной симметрии всех четырех входов) имеем

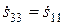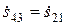, . (3.10)

Метод синфазного и противофазного возбуждения может быть обобщен на симметричные многополюсники с любым четным числом входов.