Матрица рассеяния каскадно соединенных многополюсников.

Метод декомпозиции

Универсальным методом расчета устройств СВЧ является разбиение ‑ декомпозиция сложного устройства на ряд более простых устройств, характеризуемых соответствующими матрицами параметров, что допускает их независимый анализ. Эти простые устройства называют базовыми элементами. Если характеристики базовых элементов предварительно изучены и установлены номиналы параметров, определяющих матрицу каждого базового элемента, то анализ электрических характеристик сложной системы СВЧ сводится к проводимому по специальным алгоритмам расчету матриц параметров для объединения двух базовых элементов и более.

Для расчета низкочастотных электрических цепей достаточен набор базовых элементов из резистора (поглотителя мощности), конденсатора (накопителя энергии электрического поля), индуктивной катушки (накопителя энергии магнитного поля). На сверхвысоких частотах свойства накопления и поглощения электромагнитной энергии присущи любому элементу объема анализируемого устройства и выделение базовых элементов становится не столь однозначным.

Традиционный подход к декомпозиции устройств СВЧ предусматривает замену каждого выделенного базового элемента некоторой схемой замещения, состоящей из сосредоточенных элементов 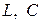и и 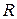отрезков линии передачи. Электродинамические расчеты базовых элементов проводят заблаговременно, а результаты представляют в виде приближенных формул и таблиц, определяющих связь номиналов в схеме замещения с геометрическими размерами базового элемента, длиной волны и параметрами магнитодиэлектриков. Преимуществами такого подхода являются универсальность, схожесть с теорией низкочастотных цепей, а также наглядность представлений о функционировании сложных устройств СВЧ, достигаемая за счет разумной идеализации схем замещения. Недостатками традиционного подхода являются потеря точности при использовании упрощенных схем замещения и трудности в количественной оценке погрешностей расчета.

Эти недостатки успешно преодолеваются при формальном электродинамическом подходе, ориентированном на применение мощных ЭВМ. Здесь осуществляется декомпозиция устройства СВЧ на ряд базовых элементов в виде геометрических конфигураций, допускающих аналитическое или численное определение матрицы параметров путем решения уравнений Максвелла при заданных граничных условиях. Последующее нахождение матрицы параметров сложного устройства (рекомпозиция) осуществляется по точно таким же алгоритмам объединения многополюсников, как и при традиционном подходе на основе схем замещения. Электродинамический подход в принципе позволяет выполнять расчеты с любой требуемой точностью, однако при этом теряется наглядность анализа и происходит сужение класса устройств, рассчитываемых по конкретной вычислительной программе.

Между традиционным и электродинамическим подходами нет глубоких принципиальных различий, и поэтому в основу последующего изложения методов анализа на основе принципа декомпозиции положен традиционный подход на основе схем замещения базовых элементов. При этом следует различать два уровня декомпозиции: 1) представление укрупненных базовых элементов СВЧ в виде схем замещения из отрезков линий передачи и элементов 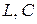и 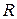; 2) разбиение тракта СВЧ на укрупненные базовые элементы и использование алгоритмов объединения многополюсников.

Матрица рассеяния каскадно соединенных многополюсников.

Принцип декомпозиции может быть использован для нахождения матриц рассеяния любых линейных устройств, образованных поочередным соединением базовых элементов. При этом заданная идеальная матрица рассеяния многополюсника представляется как результат объединения нескольких матриц рассеяния более простых многополюсников.

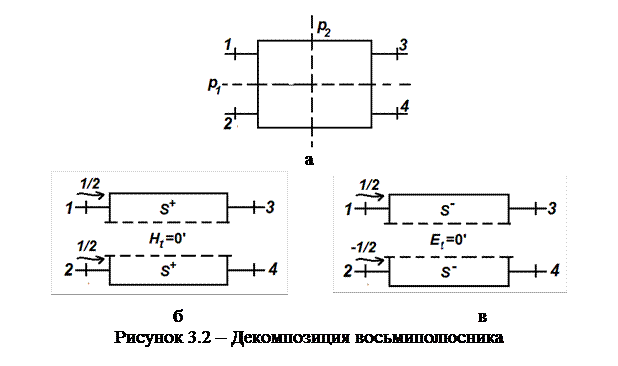
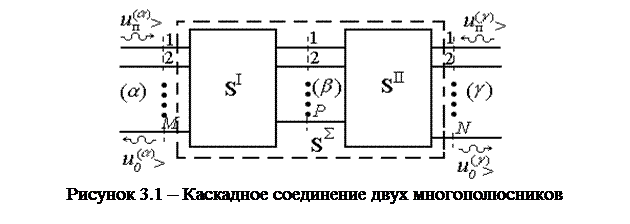Наиболее общая схема каскадного соединения двух многополюсников представлена на рисунке 3.1. Каждый многополюсник имеет группу входов, не участвующих в соединении (у первого многополюсника таких входов М, у второго N) и группу соединяемых входов числом Р. Если второй многополюсник не имеет «свободных» входов (N=0), то он является просто многовходовой нагрузкой первого многополюсника.

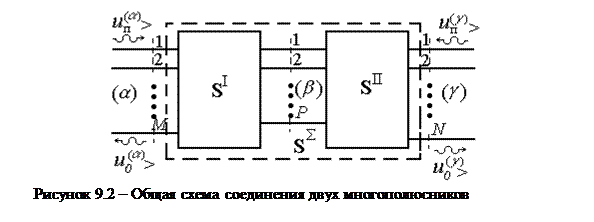Каждый из многополюсников имеет группу входов, не участвующих в соединении (у первого многополюсника число таких входов равно M, у второго N), и группу соединяемых входов, число которых равно P. В частности, многополюсник I может иметь один свободный вход и P соединяемых входов, для которых многополюсник II представляет P-входную комплексную нагрузку (случай, соответствующий распределительной системе многоэлементной ФАР, нагруженной на комплексные входные сопротивления излучателей).

Для определения S^S применяют следующую нумерацию входов: группа входов a, объединяющая все свободные M входов первого многополюсника; группа входов b, объединяющая P входов, участвующих в соединении, и, наконец, группа входов g, объединяющая N свободных входов второго многополюсника:

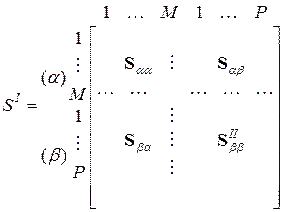; (3.1а)

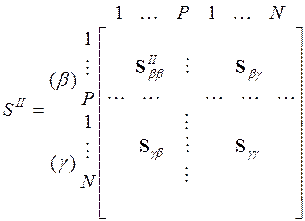, (3.1б)

где каждая из квадратных матриц S^I (порядка M+P) и S^II (порядка P+N) представлена в виде четырех блочных матриц.

Матрица рассеяния S^S представляется при этом в виде

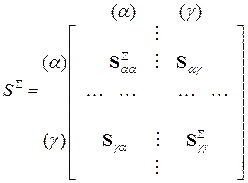, (3.2)

где ; ;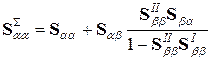

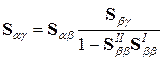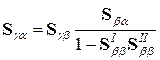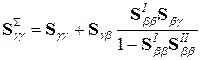; . (3.3)

При использовании выражений (3.1)‑(3.3) следует иметь в виду, что, во-первых, процедуре объединения многополюсников должна предшествовать операция упорядочения нумерации входов. Во-вторых, соединяемые входы представляют собой плоскости отсчета фаз, принадлежащие одной и той же линии передачи, т.е. нельзя непосредственно соединять между собой различные линии передачи. Стык различающихся линий передачи является отдельным устройством и должен учитываться соответствующей матрицей параметров. В-третьих, сдвиг во входных линиях передачи плоскостей отсчета в новые положения приводит к изменению матриц параметров.

Для некоторых разновидностей соединяемых многополюсников формулы существенно упрощаются и могут быть использованы при получении аналитических выражений для элементов матриц рассеяния укрупненных базовых элементов СВЧ. Рассмотрим характерные случаи.

1. Один из многополюсников согласован и развязан по всем соединяемым входам. Если имеют место согласование и развязка групп входов 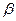либо первого, либо второго многополюсника, то формулы (3.3) принимают вид:

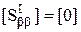при при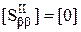

, ,

, ,

, ,

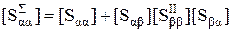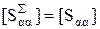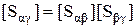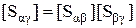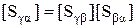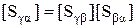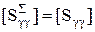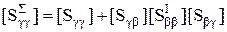, . (3.4)

Недиагональные блоки матрицы рассеяния объединенного многополюсника, называемые блоками передачи, могут быть вычислены как произведения соответствующих блоков матриц рассеяния отдельных каскадов.

2. Матрица рассеяния многополюсника при подключении к одному из входов заданной нагрузкиимеет вид

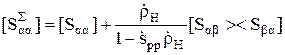. (3.5)

Таким образом, при подключении к многополюснику нагрузки матрица рассеяния уменьшает свой порядок на единицу.

Если в качестве многополюсника фигурирует четырехполюсник, то выражение (3.5) преобразуется в формулу для входного коэффициента отражения четырехполюсника с заданной нагрузкой

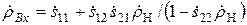. (3.6)

При подключении к входам многополюсника нескольких нагрузок преобразование матрицы рассеяния многополюсника можно производить последовательно, используя каждый раз формулу (3.5) и понижая порядок матрицы рассеяния на единицу. При подключении поглощающих нагрузок в недиссипативный многополюсник результирующая матрица рассеяния теряет свойство унитарности.