Постановка задачи интерполяции. Кусочно – линейная интерполяция

Кусочно – линейная интерполяция. Кубический интерполяционный сплайн. Глобальная интерполяция. Полином Лагранжа второго и третьего порядка.

Аппроксимировать – это означает "приближённо заменять". Допустим, известны значения некоторой функции в заданных точках. Требуется найти промежуточные значения этой функции, получим так называемую задачу о восстановлении функции. Кроме того, при проведении расчетов сложные функции удобно заменять алгебраическими многочленами или другими элементарными функциями, которые достаточно просто вычисляются (задача о приближении функции).

Постановка задачи интерполяции.

На интервале 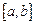заданы точки 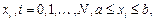и значения неизвестной функции в этих точках 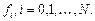Требуется найти функцию 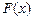, принимающую в точках 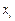те же значения 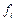Точки называются узлами интерполяции, а условия 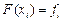– условиями интерполяции. При этом 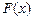ищем только на отрезке 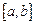. Если необходимо найти функцию вне отрезка, то - это задача экстраполяции. Пока мы будем рассматривать только интерполяционные задачи.

Задача имеет много решений, т.к. через заданные точки 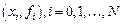можно провести бесконечно много кривых, каждая из которых будет графиком функции, для которой выполнены все условия интерполяции. Для практики важен случай аппроксимации функции многочленами, т.е.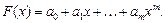

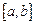Все методы интерполяции можно разделить на локальные и глобальные. В случае локальной интерполяции на каждом интервале строится отдельный полином. В случае глобальной интерполяции отыскивается единый полином на всем интервале . При этом искомый полином называется интерполяционным полиномом.