Кубический интерполяционный сплайн.
Слово сплайн (английское слово "spline") означает гибкую линейку, используемую для проведения гладких кривых через заданные точки на плоскости. Форма этого универсального лекала на каждом отрезке описывается кубической параболой. Сплайны широко используются в инженерных приложениях, в частности, в компьютерной графике. Итак, на каждом i–м отрезке  ,
, 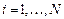 , решение будем искать в виде полинома третьей степени:
, решение будем искать в виде полинома третьей степени:
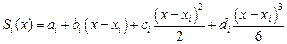 ,
,
Неизвестные коэффициенты 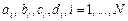 , находим из:
, находим из:
• условий интерполяции: 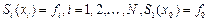 ,
,
• непрерывности функции 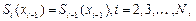
• непрерывности первой и второй производной:
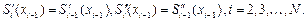
Учитывая, что 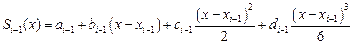 , для определения 4N неизвестных получаем систему 4N–2 уравнений:
, для определения 4N неизвестных получаем систему 4N–2 уравнений:
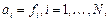
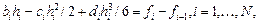
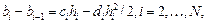
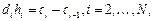
где 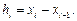
Недостающие два уравнения выводятся из дополнительных условий: 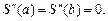 Можно показать, что при этом
Можно показать, что при этом 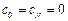 . Из системы можно исключить неизвестные
. Из системы можно исключить неизвестные 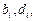 получив систему N+1 линейных уравнений (СЛАУ) для определения коэффициентов
получив систему N+1 линейных уравнений (СЛАУ) для определения коэффициентов 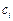 :
:
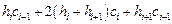 =6
=6 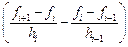 , i=1, 2,…, N–1. (11.1)
, i=1, 2,…, N–1. (11.1)
После этого вычисляются коэффициенты 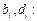
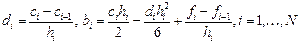 (11.2)
(11.2)
В случае постоянной сетки 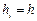 эта система уравнений упрощается.
эта система уравнений упрощается.
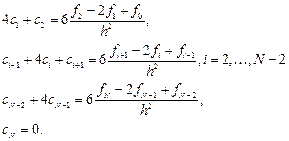
Данная CЛАУ имеет трехдиагональную матрицу и решается методом прогонки. Коэффициенты 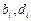 определяются из формул:
определяются из формул:
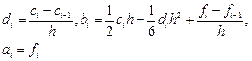
Для вычисления значения 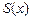 в произвольной точке отрезка
в произвольной точке отрезка 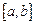 необходимо решить систему уравнений на коэффициенты
необходимо решить систему уравнений на коэффициенты 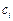 ,
, 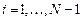 , затем найти все коэффициенты
, затем найти все коэффициенты 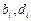 . Далее, необходимо определить, на какой интервал
. Далее, необходимо определить, на какой интервал 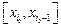 попадает эта точка, и, зная номер
попадает эта точка, и, зная номер 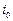 , вычислить значение сплайна и его производных в точке
, вычислить значение сплайна и его производных в точке 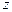 .
.
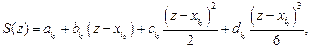
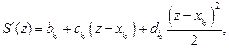
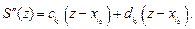
Пример .
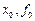
| 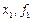
| 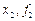
| 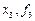
| 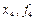
| |
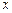
| 0 | 1/4 | 1/2 | 3/4 | 1 |
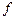
| 1 | 2 | 1 | 0 | 1 |
Требуется вычислить значения функции в точках 0.25 и 0.8, используя сплайн – интерполяцию. В нашем случае: 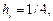
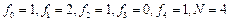
Выпишем систему уравнений для определения 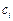 :
:
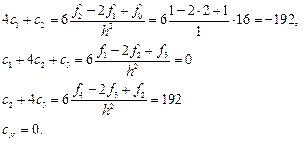
Решая эту систему линейных уравнений, получим:
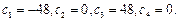
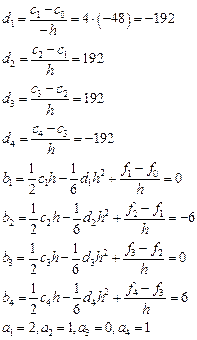
Рассмотрим точку 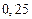 , которая принадлежит первому отрезку, то есть
, которая принадлежит первому отрезку, то есть 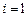 . Следовательно, получим,
. Следовательно, получим,
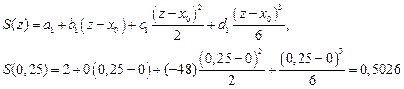
Рассмотрим точку 0.8, которая принадлежит четвертому отрезку, то есть 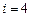 .
.
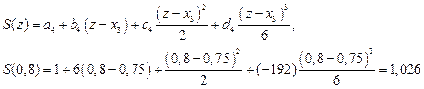
Дата добавления: 2015-11-06; просмотров: 922;
