Критериальное уравнение движения вязкой жидкости

Оно представляет собой функциональную зависимость определяемого критерия от определяющих критериев и симплексов геометрического подобия.

В общем виде критериальное уравнение движения вязкой жидкости имеет следующий вид:

Eu = f(Re,Fr,Ho,Г₁,Г₂,Г₃…)

Г — геометрические симплексы подобия.

Частные случаи:

1. Для безнапорного установившегося течения вязкой жидкости:

Eu = f(Re,Fr,Ho,Г₁,Г₂,Г₃)

2. Для установившегося движения жидкости:

Eu = f(Re,Fr,Г₁,Г₂,Г₃…)

3. Для установившегося напорного движения жидкости в прямой трубе:

Eu = f(Re,Г₁,Г₂)

4. Для напорного установившегося движения на местном сопротивлении (внезапное расширение или сужение):

Eu = f(Re,Г₁)

Определение гидравлических сопротивлений
в прямых трубах (определение путевых потерь)

Рассмотрим установившееся напорное течение вязкой жидкости в прямой трубе.

Eu = f(Re,Г₁,Г₂) = f(Re,l/d,D/d)

В связи с тем, что с увеличением длины трубы возрастают потери, симплекс Г₁ вынесем из-под функциональной зависимости:

Обозначим: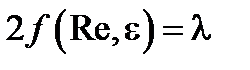

Тогда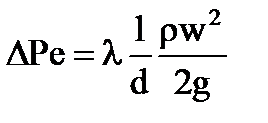

Отсюда: 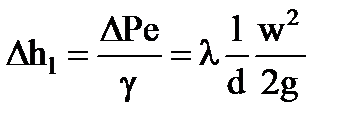— формула Дарси—Вейсбаха для определения путевых потерь.

Коэффициент l — коэффициент путевых потерь, или коэффициент гидравлического сопротивления по длине. Он определяется по эмпирическим зависимостям, полученным на основании экспериментальных исследований, в трубах с искусственной шероховатостью в зависимости от области сопротивления.

В результате обработки экспериментальных данных, полученных при испытаниях в трубах с искусственной шероховатостью был получен график, названный графиком Никурадзе. Он показывает зависимость l от числа Рейнольдса и относительной шероховатости . При его составлении измеряли количество протекающей жидкости, меняли диаметр труб, искусственно наносили шероховатость. По полученным физическим параметрам потоков рассчитывали значение числа Рейнольдса и коэффициент путевых потерь.